Annu. Rev. Astron. Astrophys. 1997. 35: 389-443 Copyright © 1997 by Annual Reviews. All rights reserved

2.1. Predictions in the Absence of Galaxy Evolution

The "no-evolution prediction" originated as a null hypothesis used to address the most basic question: Is evolution detected? Despite its frequent use, it clearly describes an unphysical situation. The passive evolution of stellar populations (defined as that arising from stellar population changes occurring in the absence of continued star formation) alone can lead to detectable luminosity and color changes over the past few billion years (Tinsley 1972). However, the look-back time to a distant galaxy (which makes the entire subject of galaxy evolution observationally possible) is accompanied by redshift and related observational selection biases that seriously affect the empirical approach of monitoring evolution as a function of redshift in flux-limited catalogs of galaxies. For redshifts of z < 1-2, the no-evolution prediction has acted as a valuable standard baseline that incorporates these biases from which the various evolutionary differences can be compared.

To predict the observables in the empirical approach, consider a local galaxy population with a luminosity function (LF) whose form is defined by the Schechter function (1976):

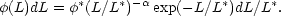(1)

Here, ^* is a normalization related to the number of luminous galaxies per unit volume; L^* is a characteristic luminosity; and represents the shape of the function, which determines the ratio of low luminosity to giant galaxies. The mean luminosity density for the Schechter function is

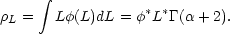(2)

Assuming that the LF is independent of location and galaxies are distributed homogeneously, the integrated source count to apparent magnitude m in the nonrelativistic case is given by

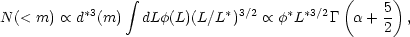(3)

where d^*(m) is the limiting depth of the survey for a L^* galaxy.

Equation 3 shows that the count normalization depends not only on ^* but also on a good understanding of L^* and . Recent determinations of the local field galaxy LF (Loveday et al 1992, Marzke et al 1994, Lin et al 1996, Zucca et al 1997) are somewhat discrepant in all three parameters. It is also important to determine the LF as a function of morphology or color because the visibility of the different galaxy types is affected by redshift bandpass effects. Color-based local LFs have been discussed by Metcalfe et al (1991) and morphological-based ones by King & Ellis (1985), Loveday et al (1992), Marzke et al (1994).

The Schechter formula need not be adopted to make predictions. One could simply use the raw luminosity-redshift data for local surveys to predict the appearance of the faint universe. Surprisingly, this has not been done. Indeed growing evidence shows that the simple Schechter expression fails to describe the full observational extent of the local field galaxy LF (Ferguson & McGaugh 1995, Zucca et al 1997). Studies of nearby clusters (Binggeli et al 1988, Bernstein et al 1995), where volume-limited samples can be constructed, also indicate significant departures from the Schechter form at luminosities M_B > -16 + 5 log h (h denotes Hubble's constant in units of 100 km s^-1 Mpc^-1). An upturn at the faint end of the field galaxy LF could make a significant Euclidean contribution (i.e. N 10^0.6m) to the faint number counts. Marzke et al's (1994) type-dependent LF suggests that such a contribution would also be quite blue.

Given a LF for type j, (M, j), the type-dependent source counts N(m, j) and redshift distributions N(z, j) in flux-limited samples are calculable once the redshift visibility functions are known. In addition to the cosmological distance modulus, the type-dependent k-correction must be determined using the appropriate SED, f (, j). Following Humason et al (1956),

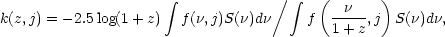(4)

where S() is the detector response function.

Progress has been limited in measuring the integrated SEDs of galaxies of different types over a wide wavelength range since the early studies of Pence (1976), Wells (1978), Coleman et al (1980) used by King & Ellis (1985), because there has been no appropriate UV satellite with which integrated large aperture SEDs can be determined. The lack of reliable k-corrections particularly affects the blue counts because, at high redshift, UV luminosities enter the visible spectral region. Kinney et al (1996) have obtained IUE-aperture spectrophotometry of 15 galaxies from 1200 Å to 1 µm (a technique attempted also by Ellis et al 1982) and claim that the small physical size of the areas sampled may nonetheless be useful if the SEDs span the range representative of the integrated galaxy light.

Ideally, the k-correction should be averaged for galaxies of a given rest-frame color rather than binned by morphology, because the correlation between morphology and color is actually quite poor (Huchra 1977) and there are added complications for spheroidal galaxies arising from luminosity dependencies (Sandage & Visvanathan 1978). Recognizing these difficulties, Bruzual & Charlot (1993), Poggianti (1997) advocated determining the k-correction from model SEDs known to reproduce the integrated broad-band colors of real galaxies. A comprehensive analysis by Bershady (1995) indicates such a technique can match five-color data of a large sample of galaxies with z < 0.3, with typical errors of only 0.04 mags. At higher redshifts, alternative routes to the k-correction have included interpolating SEDs from rest-frame colors (Lilly et al 1995) and matching spectroscopic data against local samples (Heyl et al 1997).

To what extent could k-correction uncertainties seriously affect our perceived view of the distant universe? The uncertainty in the optical k-correction for the bulk of the Hubble sequence is probably fairly small to z = 1-1.5 (Figure 1a). However, this conclusion is based on optically selected samples. Although Bershady (1995) found a few galaxies with colors outside the range expected on the basis of his modeling, for high redshift work the test should be extended into the UV. Serious errors of interpretation at fairly modest redshifts could occur if there existed a population of galaxies whose UV-optical colors did not match the model SEDs. Using balloon-borne instrumentation, Donas et al (1995) presented a large aperture UV (2000-Å) optical color distribution of a sample of galaxies selected in the UV; a significant proportion of this sample at all optical colors shows UV excesses compared to the conventional range of SEDs (Figure 2). Redshifts are needed to derive luminosity densities for these galaxies in order to quantify their possible effect on the k-corrections in use. Such inconsistencies in our understanding of the UV continua of galaxies indicate much work remains to be done in this area and also highlights the continued need for survey facilities at these wavelengths.

Figure 1. (a) Type-dependent k-corrections for the B band using two different approaches. Bold lines indicate corrections based on model SEDs that reproduce integrated broadband colors (Poggianti 1997); nonbold lines indicate corrections derived from aperture spectrophotometry analyzed in conjunction with color data (Kinney et al 1996). (b) The k-correction for ellipticals (solid lines), Sa (short-dash), and Sc (long-dash) galaxies for the UBIK photometric bands from the models of Poggianti (1997).

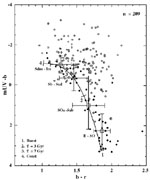Figure 2. UV (2000-Å) optical colors for a sample of UV-selected galaxies from the balloon-borne imaging study of Donas et al (1995). A significant proportion of the sample appears to have normal b-r colors but UV excesses of 1-2 mag compared to standard models (solid curve; Bruzual & Charlot 1993) used to infer k-corrections for the field galaxy population.

Inspection of the k-correction as a function of observed passband (Figure 1b) reveals the important point that the variation with type or optical color is considerably reduced in the near-infrared (Bershady 1995). There is also the benefit that, to high redshifts, the required SEDs are based on large aperture optical data. The smaller k-corrections reflect the dominant contribution of red giants at longer wavelengths in old stellar populations, and this has been used to justify a number of faint K-band surveys for evolution and cosmology (Gardner et al 1993, Songaila et al 1994, Glazebrook et al 1995c, Djorgovski et al 1995, Cowie et al 1996), on the grounds that their interpretation is less hampered by k-correction uncertainties. By implication, the observed mixture of types at faint limits is less distorted to star-forming types than is the case in optical surveys. However, if the primary motivation of a faint survey is to learn about the star-formation history of field galaxies, the gains of an infrared-selected survey are somewhat illusory. The insensitivity of the K-band light to young stars means that a deep infrared survey is primarily tracing the mass distribution of distant galaxies. When optical-infrared colors are introduced to aid the interpretation (Cowie et al 1996), the poorly understood UV continua return to plague the analysis.

The cosmological sensitivity that originally motivated the topic of galaxy counts (Hubble & Tolman 1935, Hubble 1936, Sandage 1961) enters through the luminosity distance, d_L(z) (Weinberg 1974, Peebles 1994), and the volume element, dV(z). The apparent magnitude of a faint galaxy of absolute magnitude M is determined by both the luminosity distance, d_L(z, _M, = / 3H₀ ²) in megaparsecs (Carroll et al 1992, see equation 25), and the type-dependent k-correction. Because the flux received from an apparent magnitude m scales as 10^-0.4m, the contribution that the differential counts N(m) make to the extragalactic background light (EBL) is obtained via the following (Mattila et al 1991, Vaisanen 1996):

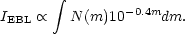(5)

Given the local properties of galaxies, the joint distribution N(m, z, j) can be predicted and compared with faint datasets. As Koo & Kron (1992) discussed, the availability of redshift data enables far more sensitive tests than for photometric data alone. Some information on the redshift distribution of faint sources can be derived from multiband colors. However, redshifts based on colors suffer from similar uncertainties to those discussed above for the k-correction. If local SEDs do not fully span those sampled in faint data, systematic errors may occur. The technique has a long history beginning with Baum (1962), Koo (1985), Loh & Spillar (1986; who sought to constrain cosmological models via volume tests). In recent years, more sophisticated techniques have been introduced that rely on spectroscopic confirmation for some subset of the sample, on the use of magnitude information to break various degeneracies (Connolly et al 1995), or on strong discontinuities in the spectral energy distributions (Guhathakurta et al 1990, Steidel & Hamilton 1992, Madau et al 1996). For extremely faint galaxies, color-based redshifts are increasingly used as a way of locating information for sources beyond the spectroscopic limits (see Section 5).