Annu. Rev. Astron. Astrophys. 1997. 35: 389-443 Copyright © 1997 by Annual Reviews. All rights reserved

5. SURVEYS BEYOND THE SPECTROSCOPIC LIMIT

Various workers have considered ways in which the mean redshift of the very faint population (say B 27, R 26, I 26, i.e. beyond normal spectroscopic limits) could be estimated statistically. One expectation might be that the bulk of such a faint population lies beyond z = 1. A redshift of unity has represented a significant barrier to the systematic study of normal galaxy populations for many years. It corresponds to the 4-m telescope limit for which spectroscopic redshifts are possible for normal L^* field galaxies, and it also marks an important transition from analyses that are, broadly speaking, independent of the cosmological framework to ones where the volume element and time-redshift relation depend critically on and . A lesson that emerges from Section 4 is that a fundamental difficulty in making progress is the need to ensure that local and high z data sets are treated similarly. As we turn to the next logical step in the observational challenge, this becomes even more the case.

5.1. Constraints from Gravitational Lensing

The suggestion that the mean redshift of the B = 27 and I = 26 population might be rather low, consistent with discussion of the break in the count slope in Section 3, first arose from the pioneering CCD exposures conducted by Tyson and collaborators (Tyson 1988, Guhathakurta et al 1990). Tyson also developed the first practical applications of gravitational lensing by rich clusters as a tool for estimating the mean statistical distance to the background population (Tyson et al 1990).

At faint magnitudes, lensing by foreground masses affects source properties by an amount that depends on the nature of the intervening lens, the relative distances to the lens and source, and the cosmological model (Blandford & Narayan 1992, Fort & Mellier 1994). The phenomenon manifests itself in several ways, depending on the geometrical configuration and lens scale. In the case of giant arcs, dense concentrated clusters of galaxies beyond z = 0.1 magnify faint sources considerably, extending spectroscopic and photometric detections to fainter limits. Certain clusters have well-constrained mass distributions, either from giant arcs and multiple images of known redshift or from indirect probes such as X-ray luminosities and velocity dispersions. The lensing shear field viewed through these clusters can provide a statistical estimate of the mean distance to sources that are too faint for conventional spectroscopy. As the technique is purely geometric in nature, it provides an independent probe of the distances to faint galaxies.

Recognizing the need to separate the dependence of the weak lensing signal on both the relative distances of source and lens and the nature of the lensing cluster, Smail et al (1994, 1995) compared the shear seen in a background population to I = 25 as measured through three clusters at different redshifts. The relatively weak shear found by Smail et al (1994) through an X-ray luminous cluster at z = 0.54 suggested a relatively low mean redshift for the population, but this is in marked contrast to the conclusions of Luppino & Kaiser (1997), who detected shear through a similar cluster at z = 0.83. Difficulties arise because this technique relies critically on measuring the absolute shear, as well as understanding the properties of the lensing cluster. A comparison of the various techniques used to estimate the shear by different workers on the same clusters is badly needed, and deep HST data of more distant clusters is also required to correct for seeing and other effects that may affect ground-based images.

Considerable progress is possible if redshifts are available for some of the lensed features, because this reduces the dependence on absolute measurements of the lensing signal (Fort & Mellier 1994). Giant arcs are strong lensing events of high magnification but offer a rather unreliable glimpse of the high redshift population. Spectroscopy is now available for about 20 cases; a few have redshifts beyond 1. Although these are galaxies found serendipitously by virtue of their location behind unrelated foreground clusters and their unlensed magnitudes are quite faint, important selection effects operate in their recognition and thus they are an unreliable statistical probe of the background redshift distribution. Strong lensing is optimal when the background source is around two to three times the angular diameter distance of the lens, and so a low frequency of high redshift arcs may simply reflect the paucity of concentrated high z clusters. At the moment, few convincing arcs have been seen in clusters beyond z = 0.5. Second, the arcs are, without exception, found as high surface brightness features in optical CCD images often by virtue of their contrasting blue color as compared with the red cluster population. Smail et al (1993, 1996) have examined the optical-infrared colors and HST angular sizes of giant arc samples and, not surprisingly, deduced that many are representative of late-type galaxies undergoing vigorous but extended star formation.

The more important role of arc spectroscopy is to further constrain the properties of the lensing cluster. The lensing geometry can then be used together with the image shapes and orientations for the fainter population of less distorted "arclets" to yield a statistical redshift for each one, assuming, on average, that they are intrinsically round sources. This "lensing inversion" technique was first developed by the Toulouse group (Kneib et al 1994) using ground-based data for the well-studied cluster Abell 370, and it has now been extended using HST images and more comprehensive ground-based spectroscopy for Abell 2218 and Abell 2390 (Kneib et al 1996). These studies suggest that the mean redshift of I < 25.5 populations cannot significantly exceed 1. In several cases, the constraints on the arclet redshifts are sufficiently tight that the predicted redshifts are worth verifying spectroscopically. In a number of such cases, Ebbels (1996), Ebbels et al (1996), Bezecourt & Soucail (1997) presented convincing evidence that the inversion technique works well. However, the construction of genuine magnitude-limited samples appears to be difficult using this method. Not only are the lensed images magnified by different amounts, but inversion is unreliable for the smallest sources that increasingly dominate the faint counts (Roche et al 1996).

To overcome difficulties inherent in analyses of distorted images, Broadhurst (1997) proposed the use of "magnification bias" or gravitational convergence. A lensing cluster enlarges the background sky, and this produces a diminution in the surface density of sources depending on the relative distances involved. For galaxy counts, the effect is in the opposite direction to the magnification described above (Tyson et al 1984, Broadhurst et al 1995). The background source counts viewed at radius r from the center of a foreground lens become

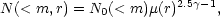(7)

where N₀(< m) represents the true counts, µ(r) is the magnification at angular radius r from the center of the lens, and = d logN / dm is the slope of the number-magnitude counts. For = 0.4, the magnification and dilution effects cancel out and no effect is seen. However, when < 0.4, the counts decrease, particularly near the critical angular radius. The location of this point depends on the relative angular diameter distances of the sources and the lens, as well as on the cosmological model. Fort et al (1997), Mellier (1997) described promising applications of this technique. As the method relies only on source counting rather than a reliable measurement of image shapes, the technique can probe to very faint limits in a controlled manner.