Annu. Rev. Astron. Astrophys. 1997. 35: 389-443 Copyright © 1997 by Annual Reviews. All rights reserved

4. ADDRESSING THE MAIN ISSUES

The aim in this section is to distill the observational phenomena discussed in Section 3 into a few key physical issues that will assist in understanding the evolutionary role of faint blue galaxies. As the greatest progress has been made in the redshift interval to z = 1, the discussion of fainter samples and the HDF is deferred until Section 5.

4.1. Uncertainties in the Local Field Galaxy Luminosity Function

The nature of the local LF was comprehensively reviewed by Binggeli et al (1988). Since then, considerable progress has been achieved through deeper, more representative local optical and infrared surveys, such as the the Stromlo-APM (Loveday et al 1992), Las Campanas (Lin et al 1996), CfA (Marzke et al 1994), SSRS2 (da Costa et al 1994), and DARS (Peterson et al 1986, Efstathiou et al 1988, Mobasher et al 1993) redshift surveys. These are utilized both as photometric databases for normalizing the galaxy counts at the bright end (Maddox et al 1990) and in deriving LFs as a function of type. Colless (1997) provides a recent summary of local LF determinations (Figure 7) to which is added the recent LF analysis of the ESO Slice Project (ESP) (Zucca et al 1997), a survey of 3342 galaxies to b_J = 19.4.

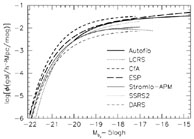Figure 7. A comparison of the Schechter function fits to various determinations of the local galaxy LF from the compilation of Colless (1997), updated to include the results of Zucca et al (1997). All LFs are placed on the bJ system using transformations given by Colless (1997).

The local normalization depends on a combination of the LF parameters (not just ^*, see Equation 3), and its value is central to the question of whether there is significant evolution in galaxy properties to z = 0.3-0.5. Early faint galaxy workers (Broadhurst et al 1988, Colless et al 1990) assumed either the Efstathiou et al (1988) or Loveday et al (1992) normalization, ^* = (1.40 ± 0.17) × 10^-2 h³ Mpc^-3, which, if too low, would increase the evolution inferred, assuming L^* and were correctly determined. Although this might be explained via a local minimum in the southern galaxy distribution, there is no convincing indication of this in the redshift distribution, and so the anomalously steep count slope found by Maddox et al (1990) brighter than B = 18 has been taken to indicate that a problem may exist elsewhere.

The Stromlo-APM survey limited at b_J = 17.2 is the largest and most well-documented local galaxy survey, but its photometry has been questioned in several recent papers. Metcalfe et al (1995a), Bertin & Dennefeld (1997) compared APM magnitudes with their own CCD-calibrated measures and detected a scale error and considerable scatter in the region 17 < b_J < 19. Bertin & Dennefeld explained this, in part, to unmeasured light fainter than the relatively bright APM isophote. However, Metcalfe et al found that high surface brightness galaxies lose more light than those of low surface brightness because of the limited dynamic range of the plate-measuring machines involved. Bertin & Dennefeld presented B-band counts whose d logN / dm slope, _16:19 in the 16 < b_J < 19 range, is 0.53 (cf 0.59 for Maddox et al 1990), a value more consistent with no-evolution expectations. It should be noted that any photometric limitations of the APM data may possibly apply also to the COSMOS-based photometry used by Zucca et al (1997) because Metcalfe et al (1995a), Rousseau et al (1996) found similar behavior in their COSMOS data. However, not all photographic photometry may be affected in this way. Weir et al (1995) present photographic counts whose slope is flatter that of Maddox et al.

The above calibrations of nonlinear photographic survey data using linear CCD detectors are the forerunners of a new generation of photometric surveys based entirely on CCDs or infrared arrays. Gardner et al (1996) presented counts in BVIK for two large northern fields covering 10 deg² and found a B-band slope _16:19 = 0.50 ± 0.03 in reasonable agreement with Bertin & Dennefeld (1997). Huang et al (1997) presented counts in BIK for a similarly sized equatorial area. Although both Gardner et al and Huang et al claim to disagree, the difference lies mostly in the bright K data. Huang et al's Table 3 gives _16:19 = 0.53. Although these survey areas are very small in comparison with the 4300 deg² of the APM survey, they nonetheless support the above claims for a photometric revision. For the = -1 Schechter function adopted by Loveday et al (1992), Gardner et al's counts indicate _B^* = 2.02 × 10^-2 h³ Mpc^-3, (i.e. a normalization about 50% higher than the APM result). A similarly high normalization emerges from the ESP results limited at b_J = 19.4 (Zucca et al 1997).

The LF and counts are also available from the extensive Las Campanas Redshift Survey (LCRS) (Lin et al 1996). Galaxies were selected in r according to a relatively bright isophote over an area of 720 deg². When allowance is made for the different photometric scale, Lin et al found a low normalization (as did Loveday et al 1992) and somewhat discrepant and L^* in comparison to those of other surveys. The latter point is significant given that the count normalization depends on all three parameters. The differences are not understood but may arise from the poor match between their actual LF and the Schechter function, possible inaccuracies in the single type-invariant k-correction used (a criticism also applicable to the ESP survey), and the outer redshift limit at which the final normalization is made.

In summary, these issues, although not entirely resolved, support a normalization increase of at least 50% over that adopted by Loveday et al (1992) and indicate that at least some photographic data brighter than B = 19 may be inaccurate in both photometric scale and possibly even in source detection (see Section 4.2 below). The normalization derived for galaxies with z < 0.1 observed to be fainter than B = 19 (Ellis et al 1996a, Cowie et al 1996) supports this upward revision, which has been incorporated in Figure 5a.

Turning to the shape of the LF and its dependence on morphology or spectral class, Driver & Phillipps (1996) have demonstrated the difficulty in estimating the faint end slope reliably from magnitude-limited redshift surveys. Regardless of size, such surveys are optimized to define the LF in the region around M^*. An additional difficulty with the deeper LCRS and ESP surveys (Lin et al 1996, Zucca et al 1997) is their reliance on a single k-correction formula for all galaxies. If, as suggested by Marzke et al (1994), the mean spectral type is a function of luminosity, systematic errors may be made in the volume correction, leading to a distortion in the derived shape.

Recognizing these local uncertainties, Koo et al (1993), Gronwall & Koo (1995) postulated the existence of a population of intrinsically faint blue star-forming galaxies whose LF has a much steeper faint end slope; this serves to minimize the evolution necessary to explain the faint galaxy counts. Limited evidence in support of an underestimated component of blue dwarf galaxies has been presented by Metcalfe et al (1991), Marzke et al (1994), Zucca et al (1997)). The hypothesis was central to the "conservative" model proposed in Koo & Kron (1992) review.

Although the faint end of the local field LF will inevitably remain uncertain to some unsatisfactory degree, to make a fundamental difference in the interpretation of the faint counts without affecting the redshift distributions at the limits now reached is fairly difficult. At the time of Koo & Kron's review, the faint redshift data only extended to B = 22.5. However, by extending the redshift surveys to B = 24, Glazebrook et al (1995a), Ellis et al (1996a), Cowie et al (1996) found only a minimal contribution of local dwarfs to the faint counts. Few 22 < B < 24 galaxies are observed with z < 0.1, in marked contrast to Gronwall & Koo's (1995) predictions (Glazebrook et al 1995a, Cowie et al 1996). Although some incompleteness remains at these limits, it is difficult to understand how this could apply to blue systems at such low redshift where the normal spectroscopic diagnostics are readily visible. Driver & Phillipps (1996) correctly pointed out that such inferences should be drawn from a comparison of an absolute number of sources seen rather than by matching N(z) distributions normalized to evolving numbers. Even so, taking the z < 0.1 redshift survey data fainter than B = 17, no convincing evidence exists to support a faint end slope steeper than = -1.2 down to at least M_B = -15 + 5 log h (Ellis et al 1996a, Cowie et al 1996).

Zucca et al (1997) presented evidence for an upturn in their local LF fainter than M_B = -17 + 5 log h, similar to trends observed for cluster LFs (Bernstein et al 1995). Although there is no reason to suppose the field and cluster LFs should be the same, as the faint end of the cluster galaxy LF is more reliably determined (given the volume-limited nature of that data), the suggestion is an important one. However, the upturn identified by Zucca et al is based on 37 galaxies fainter than -16 and only 14 fainter than -15. The implications of such a LF upturn in the apparent magnitude range probed by the redshift surveys would be very small. Thus there is no conflict between this result and the local LF limits provided by the faint redshift surveys. However, a significant contribution to the counts from this upturn would not commence until B = 26 [cf model (c) of Driver & Phillipps 1996]. The sub-Euclidean number count slope beyond B = 25 (Figure 5a) provides a further constraint on such a dwarf population.

In conclusion, much work is still needed to verify the detailed form of the local LF. The large-scale redshift surveys underway at the AAT and shortly with the SDSS to B = 19-20 will make a big improvement, provided that their photometric scales are robust. However, despite these uncertainties, the deeper redshift surveys now available indicate that a poorly understood faint end slope fainter than M_B = -15 + 5 log h is unlikely to seriously distort our understanding of the faint counts to B 26.