Annu. Rev. Astron. Astrophys. 1988. 36: 539-598 Copyright © 1998 by Annual Reviews. All rights reserved

3. ORIGIN OF JETS: THE BLACK HOLE CONNECTION

The phenomenology of AGNs, namely their exceedingly large powers (up to 10⁴⁷ erg s^-1) and concentration in small volumes ( 10^-3 pc), leads to consideration of models for jet formation based on processes around supermassive black holes (M 10⁷ M) (Rees 1984). Other suggested origins, namely star clusters, pulsar clusters, and spinars, appear to be inadequate to explain the total power, the long-term stability of quasars and radio galaxies, and short-term variability. The launch and collimation of supersonic (eventually relativistic) outflows from supermassive black holes can originate from two distinct mechanisms: (a) accretion of matter onto the black hole, liberating gravitational binding energy that is transferred to matter flung along the rotational axis; (b) electrodynamic processes, tapping black hole rotational energy and feeding it into large-scale magnetic fields. In both cases, the global picture leads to the formation of twin opposite jets as in the early proposal by Blandford & Rees (1974).

3.1. Collimated Outflows from Accretion Disks

The structure of gaseous, magnetized or unmagnetized disks is reviewed by Papaloizou & Lin (1995). Two characteristic configurations can be obtained analytically by solving the structure equations: (a) thin disks and (b) thick disks or tori, depending on whether the energy dissipated into the plasma by stresses can be rapidly radiated away or if the local pressure is competitive with gravity instead (Begelman et al 1984). In both cases, the activity at the disk surface creates a hot corona that drives winds along the rotation axis.

HYDRODYNAMIC WINDS    Hot matter at the surface of a disk can be accelerated outwards against the gravitational pull of a compact core of mass M_h by hydrodynamic pressure forces. This idea was first applied to jet acceleration by Blandford & Rees (1974) in the twin-exhaust model whose physics is derived from the stellar wind theory. Among the many subsequent papers, we refer to Fukue & Okada (1990), who presented a complete axisymmetric solution of the balance equations along and perpendicular to streamlines (Bernoulli and Grad-Shafranov equations, respectively), also including the effect of centrifugal forces generated by the disk rotation. In cylindrical geometry (r, , z) with ds as a line element along a streamline and dn perpendicular to it, these equations are

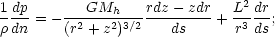(1)

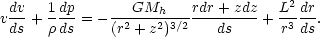(2)

where L is the specific angular momentum. Energy is injected into each streamline at the base on the disk, and a flow pattern is set up that crosses transonic surfaces to produce a supersonic wind. If the temperature distribution on the disk is flatter than 1 / r_e (r_e is the equatorial distance), the gas ejected into streamlines close to the axis is gravitationally confined and forms a corona, while the gas on external streamlines can form a wind. The opposite is true for a temperature distribution steeper than 1 / r_e. These two patterns correspond to hollow jets and well-collimated jets, respectively. The flow goes through multiple critical points, passing from subsonic to supersonic and vice versa several times with formation of shocks. The novelty of these solutions with respect to the original twin-jet model is the possibility of studying the wind solution stability and especially of bringing the first critical point very close to the core and immediately making the jet supersonic, as is observed. The link between jets and disks in the hydrodynamic models is only through the injection of energy at the base of streamlines. There is no direct back-reaction from the jets to the disk.

MAGNETOHYDRODYNAMIC WINDS    Magnetohydrodynamic (MHD) winds are an important source of advection losses from disks; they occur in the presence of an initial poloidal magnetic field anchored in the accreting material that is wound up by rotation of the disk and generates a collimating toroidal field. Thus accretion disks can naturally drive winds by centrifugal or magnetocentrifugal mechanisms (Mestel 1961, Weber & Davis 1967, Sakurai 1985). The set of MHD nonlinear partial differential equations is

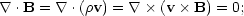(3)

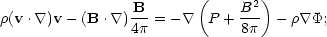(4)

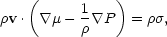(5)

where µ is the specific enthalpy and the specific heating/cooling rate. Steady-state solutions for the full two-dimensional (2-D) problem of jet acceleration from accretion disks exist for the axisymmetric case only. In this case, the set of MHD equations can be reduced to two coupled equations, the Bernoulli and Grad-Shafranov (or transfield) equations, which fully describe the wind dynamics along and across streamlines, respectively. However, these equations are formidably difficult, and some simplifying assumptions must be adopted. The main problem encountered is the presence of several critical points where equations become singular. Physically acceptable solutions must go through these points smoothly. In one-dimensional geometries, they correspond to the flow reaching the characteristic propagation speeds in the fluid (Alfvènic, slow, and fast magnetosonic); in 2-D geometries, this is no longer true for the bulk velocity but applies to specific velocity components (Tsinganos et al 1996).

Self-similar solutions: the Blandford & Payne model    The seminal paper in the context of magnetized disks and jets is by Blandford & Payne (1982), who found self-similar steady-state solutions of the ideal MHD equations of a cold, axially symmetric magnetospheric flow from a Keplerian disk. They assumed that the disk is threaded by open poloidal magnetic field lines corotating with the disk at the Keplerian velocity; in cylindrical coordinates (r, , z),

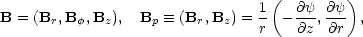(6)

where is the flux function. Total magnetic field lines are wrapped around = constant magnetic surfaces. Matter is centrifugally driven outwards in the corona and is frozen along field lines v = k() B_p / 4 + r () , where k is a structure constant and the angular velocity; k and are related as (B ^. )k = (B ^. ) . The second term implies that a toroidal field is generated:

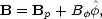(7)

which becomes dominant at large radii close to the rotation axis and consequently collimates the flow into a jet. The self-similar solutions are obtained with scaling in terms of the radial distance from the center:

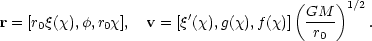(8)

For a fixed colatitude = z/r (i.e. same ), all physical quantities scale with the spherical radius, and the MHD equations reduce to a second-order differential equation in for the Alfvènic Mach number v / v_A, v_A = (B² / 4 )^1/2, and a first-order equation for the field/streamline geometry. Both equations have singular points and are studied with the above-mentioned technique of wind solutions. Physical solutions must cross singular points with regularity; the study of the topology of these critical points is rather involved and defines the characteristics of solutions. In fact, the Blandford & Payne solutions are not imposed to cross the fast magnetosonic point, and this causes a collapse of the solutions on the symmetry axis at large distances (eventually at infinity).

Blandford & Payne found two classes of collimated wind solutions depending on the final flow velocity: (a) fast magnetosonic winds with paraboloidal asymptotic streamlines and (b) trans-fast-magnetosonic winds that focus onto the rotation axis. In the first class about one third of the energy is carried as bulk kinetic energy and two thirds as Poynting flux; the second class is instead dominated by the kinetic flux and in this sense is very interesting, although it has the drawback of an excess of pinching force corresponding to a divergence in the electric current on the axis. Far from the axis, the flow continues its free expansion and is instrumental in extracting angular momentum from the system by magnetic torque. Even a small mass loss can carry a large specific angular momentum given the large lever arm of the field acting on the matter.

Other radial self-similar solutions have been studied by Contopoulos & Lovelace (1994), Pelletier & Pudritz (1992), Rosso & Pelletier (1994). In particular Contopoulos & Lovelace derived a relation between the shape of streamlines and the poloidal current consistent with the magnetic structure. Also, the Blandford & Payne model has been extended to the special relativistic case by Li et al (1992), which shows that a kinetic energy flux comparable to the Poynting flux can be obtained. Contopoulos has proposed a steady solution for jets without imposing an original poloidal field (Contopoulos 1995). A toroidal component originally present in the disk is increased by differential rotation. The strong pressure gradient between the disk (large B) and the corona above it (B 0) ejects plasma perpendicular to the disk. For this to happen, the vertical velocity at the surface of the disks must be comparable to the Keplerian velocity v_z0 ~ v₀. The ejected plasma convects azimuthal magnetic field and is self-collimated.

A different type of scaling has been proposed by Tsinganos, Trussoni, and Sauty (Sauty & Tsinganos 1994, Trussoni et al 1996, Tsinganos et al 1996), in which latitudinal self-similarity is used with all physical quantities expressed in separable form. In particular, the magnetic potential is written as

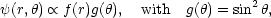(9)

and the Bernoulli and Grad-Shafranov equations for f(r) are obtained. This scaling permits a better representation of the regions around the rotation axis of the system that are singular in the Blandford & Payne solution. Solutions correspond to super-Alfvènic winds, and one class provides self-confined outflows: After an initial quasi radial expansion, poloidal streamlines undergo some oscillations and then settle into a cylindrical pattern. Also note that these solutions do not require the use of a polytropic equation of state; in fact, they correspond to a given profile of the streamlines in , which fixes the profile of the propagation channel. The heating/cooling conditions to maintain the outflow (i.e. the local equation of state) can be derived a posteriori from the solutions, in order to determine whether they are physically reproducible.

Another class of MHD winds is based on simplifying the Grad-Shafranov equation, with the consequence, however, that solutions are valid only in restricted regions. For instance, close to the equatorial plane, the flow can be modeled in thin cylindrical shells by averaging physical quantities in the direction perpendicular to the axis (Lovelace et al 1991).

Persistence of the bead-on-wire configuration    The connection between disks and jets is through the transfer of angular momentum. This allows the stability of disks and is the driving element for the spontaneous initiation of outflows. However, the field structure must be maintained in conditions to have flux lines inclined at 60° or less to the disk plane. Advection of field lines by supersonic mass flow tends to increase the inclination angle; resistive or ambipolar diffusion has been proposed to balance this effect, but in fact the angle is likely to move very close to 90° (Königl 1989, 1994). Consequently other ways must be found to launch and maintain a wind.

Ferreira & Pelletier (1993a, b, 1995) have shown that, taking into account viscous and magnetic turbulent effects in the disk plasma, the disk magnetic pressure develops a vertical component that pushes matter to the surface, leading to a continuous transition from the resistive plasma disk to the ideal MHD jet.

Shu et al (1994) have proposed that MHD winds exist only along field lines originating from the inner edge of the disk, where the central object field lines penetrate into the disk and almost corotate with it: The corotation radius is R_cor = (GM / _star²)^1/3. The disk is actually truncated inside this radius, as matter diffuses across the magnetic field (by microscopic mechanisms of ambipolar diffusion and ohmic dissipation), bends its lines inward, and accretes onto the central object. Also outside R_cor, matter diffuses onto field lines but bows them outward, transferring angular momentum to the disk, which can then reach super-Keplerian velocities and reaches an ideal configuration to start a funnel flow. This mechanism is referred to as magnetocentrifugal acceleration. For large accretion rates, the corotation radius moves close to the central object, which is forced to rotate at breakup conditions.

Recently, Contopoulos (1996) initiated the study of general solutions for axisymmetric flows without imposing E = 0, i.e. the poloidal velocity parallel to the poloidal magnetic field. This condition allows the magnetic field to be advected by the accretion flow and accumulated onto the axis of symmetry.

Relativistic flows    Camenzind (1986) has pointed out that, when dealing with fast rotators and a strong gravitational field, use of the full machinery of the general relativistic MHD theory is unavoidable. Relativistic winds have the same critical points as the nonrelativistic ones: slow magnetosonic, Alfvènic, and fast magnetosonic points. A wind equation can be obtained along the flux tube. Camenzind showed that up to ~ 80% of the initial Poynting flux at the base of the flux tube is converted into kinetic energy beyond the light cylinder and the wind velocity reaches Lorentz factors up to _bulk ~ 8. A current I is carried by the wind and is essentially determined by the total angular momentum lost through the outflow.

Radiation pressure acceleration    Radiation-supported thick accretion disks have been studied for a way to stabilize them against the Papaloizou & Pringle instability (Frank 1979, Meier 1979). In addition, deep funnels, replenished by ultraviolet photons from the walls with a net outward momentum component, produce bulk acceleration of a wind by radiation pressure. Ferrari et al (1985) discussed the quasi-2-D hydrodynamic problem of relativistic equilibrium flows for given profiles of the propagation channels. Solutions exhibit many critical points. In particular, the sudden expansion at the exit of the funnel brings the first critical point close to the nucleus. The jet thrust is not constant but decreases in the subsonic regime and increases in the supersonic regime. In fact, the surface of the jet is not parallel to the flow, and this corresponds to an external pressure force acting consistently on the field. Where the channel narrows (widens), the flow slows down (accelerates). Nobili (1998) consistently solved the radiation transport equation in the funnel, extending the results to the optically thick case. In all models related to acceleration by radiation pressure, the critically limiting factor is Compton drag by the same radiation. Particles moving at large velocities along the funnel overtake the photons emitted by the walls and have strong Compton losses. In fact, the asymptotic flow velocity cannot exceed a Lorentz factor _bulk 2. A solution to this problem has been proposed by Ghisellini et al (1990), who considered the possibility that clouds of electrons in the flow can synchrotron self-absorb the radiation from the disk or funnel. In this case, absorption is selective so that red-shifted photons fall below an absorption cutoff and therefore cannot brake the flow. Lorentz factors up to _bulk ~ 10 are attained.