Annu. Rev. Astron. Astrophys. 1988. 36: 539-598 Copyright © 1998 by Annual Reviews. All rights reserved

4.1. Global Dynamics of Confined Jets

The propagation of a laminar jet confined by external agents in stationary hydrodynamic conditions is governed by the mass and momentum conservation laws. In the Newtonian, nonrelativistic limit and for a polytropic gas P = K ,

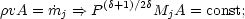(12)

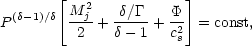(13)

where M_j is the flow Mach number, the gravitational potential, the adiabatic index of the gas, and _j the mass discharge. Equations 12 and 13 can be solved in the limit of given jet power and discharge _j. The cross-sectional area typically shows a minimum value for P_min ~ (1/2)P₀ (P₀ is the speed at the base of the flow, the stagnation point), where the jet speed becomes transonic. An adiabatic jet accelerates to supersonic speed passing through a converging nozzle. In the subsonic part of the flow, pressure and density are approximately constant, and A v^-1 (Blandford & Rees 1974).

For the large-scale hypersonic part of the flow, M_j >> 1, Equations 12 and 13 give M_j P^(1-)/2 and A P^-1/, implying v = const; for an adiabatic flow = 5/3, the scaling is M_j P^-4/5 A^-1, A P^-3/5. Pressure distribution in galaxies can be modeled as P_ext r^-n (here r is the distance from the core), and the angle subtended by the jet width as seen from the nucleus decreases as ~ A^1/2 r^-1 r^(n-2)/2. For an adiabatic flow in a halo with n = 2, the opening angle is ~ r^-2/5. Therefore steady jets can be collimated even though their area expands. On the other hand, the estimated equipartition pressure inside a jet scales as P A^-2/7, i.e. falls much less rapidly than the equilibrium solution P A^-5/3. This means that some form of internal dissipation must favor collimation.

A more complete analysis of the global dynamics of jets that takes into account confinement in channels, nonthermal momentum deposition or subtraction by external fields (radiation, plasma waves, etc) and in extended gravitational potential wells has been developed in compressible hydrodynamics by Ferrari et al (1985). They discussed quasi-2-D solutions of the problem of relativistic equilibrium flows for given profiles of the propagation channels, obtaining an equation for the flow velocity along the rotation axis:

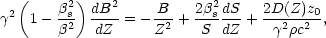(14)

where

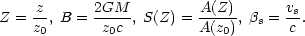(15)

The first term on the right-hand side is the gravitational term. The second is very interesting: It easily can be derived that when the channel S(Z) expands more (less) rapidly than spherically ( Z²), its walls will deposit (subtract) momentum. The last term indicates momentum addition by external forces; for the case of radiation in the limit of optically thin plasma,

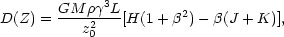(16)

where H, J, and k are the momenta of the radiation field.

Relativistic flows from accretion funnels exhibit many critical points, as compared with the single critical point (de Laval nozzle) of the nonrelativistic hydrodynamic wind solution. In particular, the sudden expansion at the exit of the funnel brings the first critical point close inside the nucleus. In these solutions, the thrust is not constant, decreases in the subsonic regime, and increases in the supersonic regime. In fact, the surface of the jet is not parallel to the flow, and this corresponds to an external pressure force acting consistently on the field: Where the channel narrows (widens), the flow is slowed down (accelerated).

Steady Newtonian and relativistic solutions show that variations in the channel cross section due to the physics of external confinement act exactly like momentum deposition. Additional critical points of complex mathematical topologies produce jets with several transitions from a subsonic to supersonic regime through shocks. The production of shocks is very interesting in connection with the observations of extended jets with bright knots, as they provide suprathermal particle acceleration and field compression that locally enhance nonthermal emission (see Section 6). In addition, the flow pattern depends on the profile of the extended gravitational potential outside the nucleus. In particular for adiabatic jets, a mass distribution M_gal r^-s, with s , does not allow the flow to reach a transonic point: The flow is stopped inside the galaxy (Ferrari et al 1986).