Copyright © 1998 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1988. 36:
539-598 Copyright © 1998 by Annual Reviews. All rights reserved |
5.5. Understanding Jet Microphysics
The above numerical experiments qualify the classical continuous jet model to explain the basic observational characteristics of extended radio sources. On the other hand, our quantitative understanding of the interlacing physical processes is still preliminary. For instance, the activity of the working surface and the formation and expansion of the cocoon are typical examples of boundary layer physics with instabilities, mixing, turbulence, etc. So far, these conditions have been simulated in a hydrodynamic or MHD approximation, while most of the important processes are plasma effects. On the other hand, plasma simulations are at present prohibitive over time scales of a few proton gyroradii for any available supercomputer. A possible approach that should be tested soon is a two-fluid model in which currents are included explicitly and the interaction between electrons and ions is taken into account for an explicit calculation of the transport coefficients, diffusion, resistivity, thermal conduction, etc.
Along the same lines, hydrodynamic or MHD models cannot properly represent crucial physical elements as currents and electromagnetic fields. The only attempt to deal with this problem is by Clarke et al (1986). However, those authors assumed an unmagnetized external medium so that the jet magnetic field cannot diffuse outside its boundaries and, although it insures collimation, does not participate in the formation of the boundary layer.
Benford (1978) pointed out that current-carrying jets may be naturally self-confined by azimuthal magnetic fields closing inside an extended cocoon that is transporting a return current. In such a scheme, Jafelice & Opher (1992) examined the radial evolution of the plasma discharge generated in the ambient plasma by a charged jet, assuming that the return current is diffused over an extended region defined by a balance between the gravitational pull and the effect of the Lorentz forces.
When a current-carrying jet is injected into a plasma,
electron currents are induced to flow in such a way that they oppose the
self-magnetic field
(Miller 1982).
Depending on the plasma conductivity
 ,
the induction electric field of the jet can effectively cause the net (jet
plus plasma) current to vanish. For small resistivity, the induced current
remains concentrated within the boundary layer of the jet; otherwise, it
can diffuse over a large region around the jet. This leads to substantial
differences in the physics of charged jets with respect to neutral jets.
For instance, if the jet current in cylindrical geometry is assumed to have
a form
,
the induction electric field of the jet can effectively cause the net (jet
plus plasma) current to vanish. For small resistivity, the induced current
remains concentrated within the boundary layer of the jet; otherwise, it
can diffuse over a large region around the jet. This leads to substantial
differences in the physics of charged jets with respect to neutral jets.
For instance, if the jet current in cylindrical geometry is assumed to have
a form
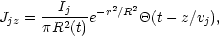 |
(25) |
with  (y) as
the step function; then the response plasma current is calculated to be
(y) as
the step function; then the response plasma current is calculated to be
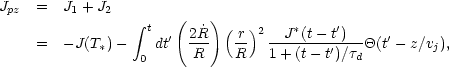 |
(26) |
where
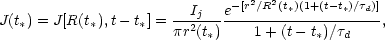 |
(27) |
with t* = z/vj
and  d
= 4
d
= 4
 R2 / c2. The consistent magnetic
field is
R2 / c2. The consistent magnetic
field is
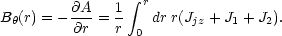 |
(28) |
If the jet contracts under the self-pinching action of the azimuthal magnetic field consistent with the carried current, then dR / dt < 0 and J2 < 0, and the return current is less, which focuses the jet more. The reverse case, which might be expected from a jet that is small at the head and grows larger behind it, J2 > 0 and the return current is preferentially driven in the region outside the radius R(t). This case may correspond to a return current sheath around the jet. The radial distribution of J2 is peaked at the edge of the jet because it is driven by the expansion/contraction of the radius.
Further behind the working surface,
the plasma current is dissipated by ohmic losses. Following
Lovelace & Sudan
(1971),
the energetics can be evaluated in terms of the Poynting theorem. If a
sharp front of considerable energy
 0
(in units of mc2) is considered, the jet velocity
changes little in the setting up of the jet current system:
0
(in units of mc2) is considered, the jet velocity
changes little in the setting up of the jet current system:
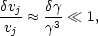 |
(29) |
and the beam current itself is almost constant
 Jj
/
Jj
/  t
t
 0 and
0 and
 Bj
/
Bj
/  t
t
 0. The jet loses
energy as
0. The jet loses
energy as
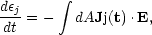 |
(30) |
where E is the induction electric field and the integral is over the jet cross section A. Therefore, the plasma magnetic field decays behind the front and does not exactly counter the jet field because of resistive decay or other dissipative effects, so that
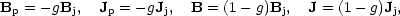 |
(31) |
with g
 1. Then, writing the energy
stored in the full self-magnetic field as
1. Then, writing the energy
stored in the full self-magnetic field as
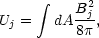 |
(32) |
we can express the quick equilibrium setup (corresponding to the current or magnetic field decay) using the Poynting theorem. We then obtain the total energy dissipated by the interaction of the current with the induced field E:
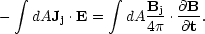 |
(33) |
Integrating over the setup time
 t with
Bj constant gives
t with
Bj constant gives
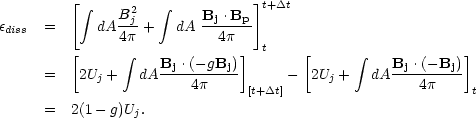 |
(34) |
A fraction (1 + g) / 2 of the total dissipated energy goes into the plasma through inductive ohmic heating, independent of the conductivity, as the return current decays; this occurs as g evolves from 1 to nearly zero as time approaches the magnetic diffusion time for the relevant distance scale. Also, a fraction (1 - g) / 2 goes into the creation of magnetic fields. All this occurs over the relevant distance for magnetic diffusion, and so such estimates are qualitatively correct if decay occurs in small filaments built up by filamentary instability very near the jet head. Energy deposition in the plasma appears as raw heating and as electrostatic fields driven by plasma instabilities, which eventually will decay into further heating. This is the final state of the electrodynamic braking of the jet. Such qualitative considerations apply to "sudden" jets, which induce return currents across their cross sections, setting up the return current path within or very near the jet area. This is because the "skin effect" of rapid induction confines currents to within a short distance of the jet radius. Such a picture applies best to very fast (perhaps relativistic) jet heads, which then are slowed quickly by inductive braking and suffer filamentary instability as well.
A different situation envisions a jet that builds gradually, so that inductive energy does not have to drive return currents within the narrow channel of the jet radius but rather does so over the expanded jet head. This requires much less energy investment, since the return current is carried by a far larger number of electrons across a broad cocoon that has a typical radius comparable to the jet head. The energy invested in setting up the return current system over a large cocoon radius is given by the ratio of the total charge carriers (electrons) carrying the jet current (Nj) compared to the number within the cocoon radius carrying the return current (Np):
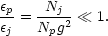 |
(35) |
Since g = 1 at the beginning of the return current setup, large cocoon radii are energetically preferred, and as g falls, more energy must be invested by the entire jet system to maintain itself against diffusion of return current outward while maintaining self-confinement at the jet core. Such scenarios suggest that jets may begin as narrow, fast (perhaps relativistic) flows, but inductive braking slows them until their heads are broad enough to develop larger inductive return current systems. Then they acquire cocoons of backflowing plasma. This links the inner jet, which is self-confined by the greater self-field near the center, to the outer cocoon, where the eventual return currents primarily flow. Such cocoons have substantial stabilizing powers, as they inhibit lateral instability by adding the cocoon mass to the jet, increasing its inertia.