Annu. Rev. Astron. Astrophys. 1988. 36: 539-598 Copyright © 1998 by Annual Reviews. All rights reserved

6.1. Evolution of the Relativistic Electron Distribution Function

Self-consistent particle acceleration and radiation loss processes have not been fully implemented in numerical dynamical codes, although radiation losses have been proven to influence the dynamics by slowing down the evolution of perturbations (Rossi et al 1997). Radiation has been generally estimated by just assuming that synchrotron emissivity is proportional to the local pressure, which is consistent with pressure equipartition between thermal and nonthermal components (Komissarov & Falle 1997).

Massaglia et al (1996b) have developed a self-consistent method to calculate numerically the time evolution of the relativistic electron component in a supersonic jet exposed to adiabatic losses, synchrotron emission, and acceleration at shock discontinuities. The numerical method solves the Kardashev equation for the relativistic electron distribution function F(E) that is assumed to move along with the thermal component dominating the dynamics:

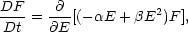(36)

of which the first term on the right corresponds to adiabatic losses, = -( ^. v) / 3, and the second to synchrotron losses, = b B²; D / Dt is the Lagrangian derivative. This equation can be solved to

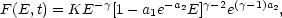(37)

subject to the condition F(E, 0) = K₀ E^- and with the integrals along the fluid element trajectory:

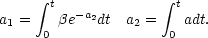(38)

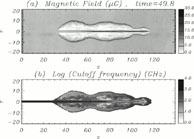
Therefore, the spectral distribution can be followed solving for a₁ and a₂ together with the system of the fluid equations in the assumption that relativistic electrons are tied up with the thermal plasma. In addition, the authors considered a systematic shock acceleration that prescribes that where the flow develops a shock discontinuity, the particle energy is increased by a given factor proportional to the shock compression. The dynamical code employed was a standard hydrodynamic PPM with a passive magnetic field whose evolution follows a scalar advection equation. Magnetic field, synchrotron emissivity, and cutoff frequency are plotted in Figure 10 for two cases of supersonic light cocoons. Calculated spectral profiles suggest that injection of high-energy particles is the critical element to reproducing observational data.

Figure 10. Synchrotron radiation from jets and cocoons: (a) M = 300, = 100; (b) M = 100, = 10 (Massaglia et al 1996b).

Ferrari & Melrose (1997) calculated the particle spectrum produced by MHD turbulence from the lower cutoff fixed by the injection mechanism and the upper cutoff related to radiation losses:

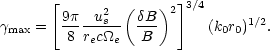(39)

With standard observational parameters for M87, u_s ~ 10^-2 c, B ~ 30 nT, r₀ ~ 6 × 10⁶ cm, and for a well-developed Kolmogorov turbulence, ( B / B) ~ 1, with energy input on the largest correlation scale L₀ = k₀^-1 cascading to smaller scales. Then k₀ r₀ ~ 2 × 10^-12 / L_{0, pc}, where we have measured L₀ in parsecs, and Equation 39 gives _max ~ 10⁶ / L_{0, pc}^1/2, which for L_{0, pc} ~ 1 is close to the required value quoted by Meisenheimer et al (1996). This indicates that turbulence must have a correlation length of at most 1 pc. This is a prediction to be tested by future high-resolution observations.