1. INTRODUCTION

1.1. A little bit of history; how magnetic fields have been measured

Until recently, the role and influence of magnetic fields in the extragalactic Universe has remained an unknown, and hence often ignored aspect of astrophysics. Most of what is known of magnetoplasma processes in astrophysics has come from solar studies - where we could make direct measurements of the field direction and strength through measurement of Zeeman splitting, and gain understanding of the role of magnetic fields in particle acceleration from the dynamic analysis of solar bursts and prominences. The observations and related theory describing the role of solar magnetic fields have developed since the Second World War.

Awareness of the existence of magnetic fields in diffuse astrophysical plasmas, i.e. beyond the solar corona, began with the discovery of synchrotron radiation (Schwinger 1949) and important energy loss process for relativistic electrons in a magnetic field. Then came the realization in the early 1950s (Alfvén and Herlofson 1950, Kiepenheuer 1950, Shklovskii 1953) that the (then) newly discovered, non-thermal emission from the interstellar medium of the Milky Way and supernova remnants is indeed synchrotron radiation, which requires both a magnetic field and relativistic electrons through the emissivity equation

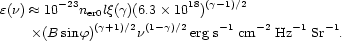(1.1)

The index describes the power law slope of the energy distribution of the relativistic electrons (n_er(E) = n_er0 E^-), () is a slowly varying function of , being unity for = +2.5, l (cm) is the line-of-sight dimension of the emitting region, is the average electron velocity pitch angle with respect to each electron's local field direction, B is the total field strength in Gauss, and is in Hz (cf Pacholczyk 1970).

As radio astronomy developed in the 1950s, the discovery of extended extragalactic radio sources (EGRS) with similar, non-thermal emission spectra meant. by implication, that they too must shine by synchrotron radiation, and hence possess an associated magnetic field.

However, from verifying the existence of a magnetic field to actually measuring the field strength is a big, and non-trivial step since, from equation (1.1), the synchrotron emissivity, although measurable, does not give us the magnetic field strength. which scales by the local number density of relativistic electrons, n_er (and/or positrons, n_pr). Obviously if we are to build magnetic fields into our understanding of galaxy formation and cosmology, we must be able to measure magnetic field strengths.

A direct way of measuring the strength of a uniform magnetic field is to measure Zeeman splitting of a radio transition in the interstellar gas.

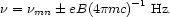(1.2)

Where _mn is a single transition, and B is in Gauss. The first successful measurements, for the interstellar H I line in absorption, were made in the late 1960s (Davies et al. 1968, Verschuur 1968). The long time between the original suggestion that an interstellar Zeeman effect should be observable (Bolton and Wild 1957) and these first detections is a measure of the technical difficulty, at the time, of conducting such measurements. Subsequent observational studies have since made great progress, and have provided considerable information on the magnetic field strength in interstellar clouds in our galaxy (see Heiles 1990 and references therein for a recent review). Unfortunately, Zeeman splitting has not been observed in external galaxies, much less in intergalactic space, because of Doppler smearing of the radio lines due to dynamical effects, combined with the rather weak field strengths.

Zeeman splitting has also been detected in the pairing of maser transitions of the OH molecule in the 18 cm band. Successful measurements of magnetic field strengths using OH Zeeman splitting were made by Zuckerman et al (1972), and more convincingly with very long baseline interferometer observations of excited OH lines near 5 cm by Moran et al (1978). However these measurements can only be made in compact H II regions and similar systems at high densities (n ~ 10⁷ cm^-3), where the magnetic fields are typically 2-10 mG and the size scales are 10¹³ to 10¹⁷ cm (Reid and Moran 1981). These, in any case interesting, measurements might at first sight seem irrelevant to the subject of extragalactic magnetic fields. However they reveal a remarkable additional fact, which may point to how galactic magnetic fields built up from primeval seed fields; namely that the sign of the magnetic field direction remains consistent over compact OH sources in the same region of the galaxy and, according to Reid and Silverstein (1990), appears to trace the large scale galactic field. Another similar, and unexpected phenomenon is the discovery by Appenzeller (1990) of an apparent alignment between the highly collimated circumstellar-scale flows from Herbig-Haro objects and the large scale interstellar magnetic field. This apparent coupling of sub-pc to kpc scale fields, originally suggested by Davies (1974), lends support to the idea that magnetic field compression occurs during protostellar contraction (Spitzer 1968, Mouchovias 1976, Mestel 1977), and that the field strength, being a few µG in the general interstellar medium (ISM) and 6 × 10^-3 G at n ~ 10⁷ cm^-3, goes as | B| n^1/2. An isotropic contraction with a frozen-in field, by contrast, would give | B| n^2/3. These results have given us some of the first quantitative indications of how magnetic fields evolve in collapsing systems. Thus they may give important clues to understanding the role of magnetic fields in collapsing galaxy systems.

Another detector of magnetic fields is Faraday rotation measure (RM) of the linearly polarized emission of radio sources, given by

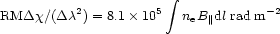(1.3)

where is the rotation (degrees) of the plane of polarization measured at wavelength (m), n_e(cm^-3) is the local density of non-relativistic electrons, B _|| the line-of-sight component of magnetic field (G), and l the path length (pc). The magnetic field strengths and baryonic matter densities in interstellar and intergalactic space are such that Faraday rotation is detectable at radio wavelengths. From (1.3) we see that, to estimate the uniform magnetic field strength from Faraday rotation, we require an independent measurement of the free electron density, and knowledge of its weighted distribution along the line of sight. For pulsars in our galaxy, this is available in the form of the dispersion measure (DM n_e dl) of pulsars. DMs can be measured from the relative pulse delay versus frequency relation, so that the ratio RM/DM gives a weighted value of the line-of-sight component of field strength along the interstellar sight line to the pulsar. This type of magnetic field measurement was first performed by Lyne and Smith (1968). Unfortunately, pulsars are too faint to observe in external galaxies, so that this method cannot be applied to the measurement of extragalactic field strengths. A possible caveat to this statement might conceivably follow from the increasing evidence for intrinsic rapid time variability - down to intra-day scales - of some very compact quasars (cf Quirrenbach et al 1991). If suitable 'time markers' in the light curves of extragalactic objects can be identified over a frequency range large enough to measure their extragalactic DM, this, combined with an RM (from simultaneous multi-frequency polarization measurements) would give a measure of the extragalactic magnetic field strength, modulo some assumptions about the field reversal scale.

In practice, and as discussed in section 5.2.1, the finite angular resolution will cause (1.3) to be an average over different lines of sight, depending on the scale of the magnetized region being measured. Since we would like to measure one line of sight, this means the higher the angular resolution, the better. If we can independently measure the density of the ionized gas associated with the Faraday rotation, and measure the field reversal scale, the magnetic field strength can be derived. Thus, a combination of RM and n_e determinations gives us the best prospect of measuring, or estimating, magnetic field strengths in extragalactic systems.

Beginning in the 1960s, Faraday RMs from linear polarization measurements of extragalactic radio sources, led to the discovery that a large scale, organized magnetic field permeates the disk of our galaxy (Davies 1968), and subsequent measurements of the RMs of ever larger numbers of (polarized) extragalactic radio sources has led to a more refined modeling of the large scale galactic magnetic field structure (Simard-Normandin and Kronberg 1980, Sofue et a1 1983, Vallée et al 1988, Clegg et a1 1992). The galactic magnetic field appears organized on a grand scale, and also has some large scale field reversal(s). Recent studies of external galaxies (cf Wielebinski 1990) indicate that all disk galaxies are permeated by large scale magnetic fields.

Apart from Faraday rotation combined with independent electron density and field reversal scale estimates, there are few prospects for directly measuring magnetic field strengths in the extragalactic universe. However, even in the absence of companion data on n_e detailed imaging of the polarized radio synchrotron emission and the RM in external galaxies, radio galaxies, and galaxy clusters has given us considerable new information on the morphology, and degree of ordering of extragalactic magnetic fields. Additionally, there are indirect and potentially powerful methods for estimating, or limiting field strengths, which we discuss in section 5.4.

Related overview articles dealing with astrophysical magnetic fields have been published by Asseo and Sol (1987), Priest (1985), Rees (1987a), and Wielebinski and Krause (1993). An interesting historical prologue to the subject has been written by F. Krause (1993). Recent and informative review articles can be found on the related topics of radio emission from normal galaxies by Condon (1992), the disk-halo connection in galaxies by Dettmar (1992), and the intergalactic medium by Fabian and Barcons (1991).