5.2. Magnetic fields associated with absorption line system in quasars

Having shown that the RM from a widespread IGM (iii) is below current levels of detectability, we now focus on what has been learned about magneto-ionic gas in discrete intervening systems (ii) at intermediate redshifts (z_a) between us and z_e, that of the emitters - the quasars. We ignore, for the moment, a source-associated component (i).

Independent evidence from optical and 21 cm absorption lines at intermediate redshifts (z_a), reveals that quasar lines of sight pass through intervening galaxy systems whose column densities, and excitation conditions, can be inferred from the equivalent widths at z_a, in suitably chosen absorption line transitions. In a combined analysis of the best available quasar RMS and absorption line data, Kronberg and Perry (1982) found a correlation between high column depth absorbers in front of quasars, and the tendency for a quasar to have an excess RM (cf also Watson and Perry 1991). This confirmed the existence of magnetic fields in galaxy systems at large redshifts. For those quasars with good estimates of free electron column density, N_e, Kronberg and Perry were able to make the first crude estimates of magnetic field strengths in these absorber system - which varied from a few µG to nearly a milligauss.

A small subset of quasar intervenors has high column density (N_HI 10²¹ cm^-2) of neutral, or near neutral hydrogen, which gives rise to damped Lyman- absorption (Wolfe 1988). This is an indicator of a galaxy disk. Combining these line equivalent width estimates with RM data, Wolfe (1988) obtains field estimates of a few µG for these systems - which are not much different from typical galactic interstellar field values.

5.2.1. The methodology of magnetic field estimates for quasar intervenor 'clouds.     The observable RM and the observationally derivable N_e, the electron column density in an intervening cloud at z_a, can be related to the cloud's magnetic field by

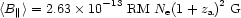(5.3)

where <B _|| > is defined by

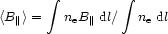(5.4)

(Kronberg and Perry 1982). At most a small number of large galaxies will intersect a typical line of sight out to z_e 3, the present-epoch density of galaxies having halos of r ~ 45 kpc is 0.017h₇₅ Mpc^-3 (cf Burbidge et a1 1977), and a fraction of current quasar samples can be expected to have no intersections with large, high column density galaxies. (For µGauss-level fields, N_e 10²⁰ cm^-2 at the current epoch is needed to produce a detectable rotation measure.) We can take equation (5.4) one step further to estimate the most likely actual magnetic field strength if a few (m) similar clouds (at approximately the same epoch) are intersected by a background quasar:

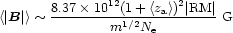(5.5)

(Kronberg and Perry 1982), where N_e are the (assumed comparable) column densities in each of the m clouds near to z_a, whose field directions are randomly orientated with respect to each other. The constant includes the expectation value of 0.5 for cos over m randomly oriented samples.

The foregoing discussion implicity assumes a unique line of sight, i.e. that the RM (and the column density) are not averages over several different sightlines to an extended illuminating quasar. In practice, the integrated RM might represent an average over several independent sight lines, if the radio source has extended structure. This fact can serve to underestimate <|B|> as determined in equation (5.5), in that the RM in one or more of the sightlines in an extended image might be significantly larger than the integrated RM (cf Perry et al 1993 for a discussion of this point). Another fact to take into account is that, because the radio structure is sometimes extended over tens to hundreds of kiloparsecs, whereas the optical emission is typically < 100 pc in quasars and AGNs, the line of sight which is relevant to N_e, may not coincide with that along which the RM was generated (equation (5.3) and (5.5)). For statistical estimates of magnetic fields in quasar absorption line systems, only integrated RMS are currently available in large numbers, so that these considerations must be allowed for in making estimates of real magnetic field strengths. Recently, high Faraday rotation images made with sub-arcsecond resolution with the VLA have provided transverse probes in RM along various lines of sight through an intervenor. This makes it easier to identify the appropriate sightline(s) to which (5.3) and (5.5) apply.

5.2.2. Magnetic field estimates from transverse probes of quasar intervenors.     High resolution RM images of the forgoing type have been made by Kronberg et a1 (1990) for 3C191, a quasar with a rich, 'associated' absorption line spectrum, i.e. absorption virtually at the redshift o f the emission lines. Such, relatively unusual, associated systems are not the typical intervening galaxies just discussed; in 3C191's case, it has been proposed to be a wind-driven shell of hot gas (seen in absorption and emission in this case) by Kronberg et a1 (1990) and Perry and Dyson (1990). The magnetic field strength in this z = 1.945 system was found to be in the range of 0.4-4 µG. Furthermore, it was found to maintain its prevailing direction over at least ~ 15 kpc - a substantial fraction of a galaxy size.

Another transverse RM probe of an intervening galaxy at z = 0.395, using the extended and polarized jet of the quasar PKS 1229-021 at z = 1.038, has recently yielded a fairly firm estimate of magnetic field strength in the intervenor of 1-4 µG (Kronberg et a1 1992). In this case, the field direction reverses every 0.7", which corresponds roughly to a spiral arm separation in a galaxy at that redshift. The spectrum of the associated quasar exhibits damped Lyman-a absorption (indicative of a galaxy disk), and a combination of absorption transitions which indicate a galaxy halo and disk, where N_e, in the disk is reasonably well measured. Combination of a detailed analysis of the optical and 21 cm absorption spectrum by Briggs et al (1985) and the RM variations established by Kronberg et a1 (1992) made it possible to give a well determined field strength, and confirm that this z = 0.395 quasar intervenor is very likely a spiral galaxy whose interstellar magnetic field strength is similar to that in our Milky Way.

5.2.3. Quasar intervenors as test objects for the galactic dynamo theory.     Because high column density H I intervenors are probably galaxy disks, firm estimates of their magnetic field strength such as that of Kronberg et a1 (1992) above, combined with their large lookback times enables us to test current ideas of field amplification and seed fields. For the above intervening galaxy at z = 0.395, the cosmological lookback time is approximately 38% of the Hubble time (for = 1). This intervenor provides one of the first available test objects for this purpose (cf also section 2.3). The fact that the field strength in this system is comparable with typical galaxy disk fields in the local universe suggests that, if this object is typical, than magnetic field amplification has not occurred over the past 40% or so of the age of the universe.

Additionally, the difference in cosmic time between the absorber-galaxy's formation time, t_form and that at its observed redshift, (t_form - t_z=0.395 for the PKS 1229-021 intervenor), can be compared with the dynamo amplification time required to amplify the field from, say the hypothesized primordial seed field strength up to the observed value of a few µG (in this case) at z = 0.395. In a Friedmann ( = 0) universe, this cosmic time difference depends strongly on , i.e. on the total matter density in the universe, and in the sense that higher (e.g. in a dark-matter-dominated universe) shortens the timespan over which the galaxy can amplify its field. Supposing that the z = 0.395 intervenor galaxy for PKS 1229-021 formed at z = 4 in a = 1 universe, Kronberg et al (1992) calculate that, if the galaxy disk dynamo amplification time is larger than one galaxy rotation, then a 4 µG field requires a seed field at t_form of at least ~ 4 × 10^-16G. For later t_form (lower z_form), the required seed fields are yet larger (unless < 1). Alternatively, if the dynamo amplification is `fast', i.e. shorter than a galaxy rotation time (see section 2.3.6), then smaller seed fields would be allowed. This result does not contradict the alternative hypothesis, namely that µG-level fields have existed in galaxies since very early epochs, and even at z 0.4 have long since saturated to the local-epoch disk field levels of a few µG .

The example of PKS 1229-021 illustrates how magnetic field strength determinations in such systems can be used to test models of slow, mean field amplification and set limits on seed fields. It shows that we are beginning to set meaningful limits at z = 0.4 to 0.5, so that measurements on similar systems at z > 1 will provide some stringent tests - especially if 1 and = 0.