2.2. Observational overview of large scale riiagneticfields in spiral galaxies

2.2.1. Current instrumental capabilities.    The improved sensitivity and polarimetric capability of both radio and optical telescopes has revealed a great deal about the morphology and extent of magnetic fields in galaxies over the past five to ten years. In this section we explain the observational methods (well described by Krause 1990), and illustrate how they can be used to reveal magnetic field morphology and strength in relatively nearby galaxies. The latter have typical projected sizes of a few to a few tens of arcminutes, so that typically 5 to 15 linear resolution elements can be obtained with large, single-dish radio telescopes at 2 cm 20 cm - the usable wavelength range for this purpose. Good, and well calibrated beam characteristics are required for polarization of these extended objects, where the telescope's beam is embedded in an extended polarized source. The 100 m Effelsberg telescope of the Max-Planck-Institut für Radioastronomie (resolution = 4.0'( / 10 cm)) has been a prime instrument for such measurements at the shorter s. At the longer wavelengths and for more distant galaxies the higher resolution of radio arrays is necessary; notably the NRAO VLA and the Westerbork Synthesis Radio Telescopes. There is a complicating difficulty with interferometers for imaging diffuse polarized emission in nearby galaxies which results from their inherent tendency to filter out the largest scale components of diffuse polarized emission. It is also sometimes difficult to deconvolve the latter from polarized sidelobe structure of the individual array antennas, since the largest images - e.g. M31 - are sometimes larger than the beam size of a single interferometer element,

2.2.2. Current knowledge of spiral galaxy disk magnetic fields.    Figure 1 shows a recent 2.8 cm (10.7 GHz) Effelsberg 100 in telescope 'magnetic field' image of the 6 Mpc distant, barred spiral galaxy Messier 83 at 68" resolution (Neininger et al 1991). The large scale coherence of the magnetic field is striking, and this is typical of the ca 20 nearby galaxies mapped thus far at some radio wavelength. A derivation of the true projected magnetic field orientation normally requires polarization images at two, and preferably more radio wavelengths, so that Faraday rotation (equation (1.3)) can be removed at each image point. At the relatively short radio wavelength of 2.8 cm a Faraday rotation of 2.4° (relatively insignificant) corresponds to a Faraday rotation measure (RM) of 55 rad m^-2 which, from our general knowledge of galaxy disk RMs, is unlikely to he exceeded at this resolution for a relatively `top-on' view of the disk. Thus, a single short polarization map such as in figure 1 gives a good approximation to the intrinsic magnetic field orientation over the galaxy.

Figure 1. A radio-optical superposition of M83, in which the normals to the maximum E-vector direction at 2.8 cm gives a good approximation of the projected magnetic field orientation at a resolution (circle at lower left) of 1.2' ( 2 kpc). Figure from Neininger et al (1991).

The fact that the polarized (synchrotron) component of the diffuse radio emission becomes fainter with increasing frequency (S / , - 0.6) underlines the `state-of-the-art' nature of the image in figure 1 which, at = 10.7 GHz, is already sensitivity limited. A higher angular resolution would further reduce the flux density per beam and hence reduce the polarized signal. An advantageous consequence of the low Faraday rotation at higher radio frequencies near 10 GHz is that differential Faraday rotation is minimized, which would otherwise cause depolarization along each bundle of sight-lines within the galaxy. Thus, the galaxy is not `Faraday opaque', which can be the case at longer s, e.g. at 20 cm (cf Neininger et al 1993 for the case of M83).

A similar large scale, organized field is revealed by polarimetry of the optical surface brightness, as illustrated in the recent image in figure 2 of NGC 1068. The overall magnetic field alignment is striking, as in the radio polarization maps. Although no information about the sign of the B-direction can be inferred from optical polarization images, their resolution is limited only by the sensitivity of the detector/telescope combination, down to the optical `seeing' limit of resolution, which is of order 1 arcsecond for a ground-based telescope. Because of the multiple causes of optical polarization, and problems of optical extinction in inclined galaxy disks, the most yielding of optical information on the magnetic field morphology are nearby, face-on galaxies like the one shown.

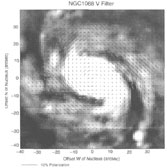Figure 2. The prevailing magnetic field orientation in the optical V-band for the galaxy NGC 1068 (S. M. Scarrott, private communication). Typical degrees of optical polarization lie in the range 0% to 5%.

Not shown in figure 1 is the Faraday rotation measure (RM), which can also tell us, at each polarization pixel, whether the field has a component which is directed into or out of the plane of the sky. Whether or not there are global reversals of prevailing magnetic field sense is an interesting question, which bears directly on the field amplification mechanism, and possibly on how the protogalactic axis was coupled (if it was) to a primeval intergalactic field. R M observations can distinguish whether the global galaxy disk field has an axisymmetric, or bisymmetric form, as illustrated schematically in figure 3. Observational discrimination between these two possibilities can be made with multi- polarization images, using a straightforward technique first suggested by Tosa and Fujimoto (1978). For the bisymmetric field case in figure 3(a), we can model the global magnetic field as a spiral (as justified from figures 1 and 2), and plot the observed RM as a function of azimuth angle () for a suitable radial zone (r_outer - r_inner) within the de-projected plane of the galaxy's disk. For an inclination angle i > 0° (face-on = 0°), a plot of RM against has four zero-crossings for a bisymmetric field galaxy, as opposed to two for an axisymmetric (non-reversing) global field morphology. This is illustrated in figure 3(c), along with data from two galaxies. Additional geometric details of the disk field can be specified, such as the pitch angle, p, of the spiral field direction, and position angle, , of the point of maximum RM on the circle, in which case the model RM- curve can be expressed as

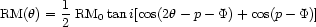(2.1)

(Tosa and Fujimoto 1978, Sofue et al 1986). A quicker observational discriminant between asymmetric and bisymmetric structure, proposed by Sofue et a1 (1985), is simply to plot the observed RM(r) along the projected major axis of the galaxy disk, from which the `signatures' of an axisymmetric and bisymmetric structure can be distinguished. This is illustrated in figure 3(b). Better still would be a detailed 2D RM map over the entire galaxy surface. Among the very few such images at the time of writing is that of NGC 6946 by Ehle and Beck (1993), which reveals a global, galaxy-scale `flip' of the RM sign between the two halves of this galaxy's disk - thus indicating an overall axisymmetric field configuration. It should be noted that the model curves in figure 3 assume purely toroidal fields in an infinitely thin disk - which is now generally realized to be unrealistically simple (cf sections 2.3, 5, 6).

Figure 3. (a) Face-on view ora model axisymmetric (left) and bisymmetric (right) magnetic field distribution in a galactic disk. (b) RM(r) measured along the major axis of the projected galaxy for the axisymmetric (left), and bisymmetric (right) case, respectively. (c) The form of the RM() distribution within an annulus of the deprojected galaxy for an axisymmetric and bisymmetric field, along with the actual data for two different galaxies. Adapted from Tosa and Fujimoto (1978) (a), Sofue et al (1985) (b), Beck (1982) (M31) and Krause et al (1989) (M81) (c).

From the available subset of nearby galaxies having RM() measurements analyzed as just described, both axisymmetric and bisymmetric configurations appear to exist. It is also increasingly apparent that some galaxies do not conform to either, including M83 in figure 1. In this connection we note that these classifications may be sensitive to the linear resolution available, and also possibly to the galaxy's inclination or disk thickness (z-height). Thus galaxy magnetic field configurations, and the classification scheme are subject to future modification. In general, global disk fields appear more aligned in the inter-am regions, and less so in the visible arms (Beck 1991), and the degree of field uniformity is anticorrelated with the intensity of CO line emission, which comes from the denser, hence starforming regions - i.e. the visible spiral arms (Bajaja et al 1990). As more detail emerges, the situation becomes more complex; for example in M31 (the Andromeda galaxy), where good linear resolution obtains due to its proximity, the patterns of Faraday rotation and field ordering do not conform on smaller scales to either a simple AS or BS model (Krause et al 1989, Beck et al 1989). A more complex pattern has also emerged in detailed studies of M83 (Sukumar and Allen 1989, 1990, Neininger et al 1993). While the magnetic field structure is generally better aligned in the outermost regions of spiral galaxies, the simple model assumptions of equation (2.1) and figure 3 are oversimplified at smaller galactocentric radii. More specifically, the form of the curves in figure 3(c) requires that the pitch angle, p , be constant over the galaxy's disk. This may not normally be so, as is already evident in M31 and M83. We discuss further observational evidence and physical reasons below, for magnetic fields directed out of a galaxy's plane. Also, systematic field reversals may be occurring which may not conform to a large scale bisymmetric field, but which may rather be due to effects which are local, and possibly transient. Thus, the field models suggested in figure 3(a) may, with future data prove to be very oversimplified; in particular they do not incorporate halo or out-of-plane fields (cf sections 2.3.5, 2.3.6).

2.2.3. Observations of magnetic fields in halos of galaxies    A datum of interest is the magnetoionic strength above the disk of our own galaxy, and in the Galactic Halo - which we can compare with the `out-of-disk' and halo magnetic fields of other spiral galaxies. Simard-Normandin and Kronberg (1980) used the (l, b) distribution of EGRS RMs to estimate the Milky Way's magnetoionic scale height, and determined a value of 1.4.kpc (full width), which is relatively insensitive to the field reversal scale. This is similar to the galactic scale height of the hot gas, 1 kpc (cf Kulkarni and Heiles 1987, Reynolds 1990). It also indicates that any Faraday RM in the halo of our galaxy is small compared with that in the disk. Information is just beginning to appear on the Faraday rotation in the higher halos of nearby spiral galaxies, however recent attempts to detect synchrotron-emitting `halos' of galaxies seen edge-on indicate full widths (to the 1% level of surface brightness) of 2-4 kpc (Klein et at 1984, Hummel 1990). This result is not inconsistent with the scale height quoted above. We note, though, that a few galaxies, those with increased star formation activity, reveal pronounced and larger halos at lower radio frequencies, in which polarized emission traces the magnetic field out to large distances above their galactic planes. These are discussed separately below (section 3.1).

Improved resolution and sensitivity to radio synchrotron emission off the disks of some normal galaxies - which were observationally selected to be edge-on for the purpose of investigating the out-of-plane field geometry - has recently provided valuable new information on the z-component of disk fields, and the orientation and degree of ordering of these fields out to large z-heights. A case in point is the edge-on galaxy NGC 891 (which is largely similar to our Milky Way). NGC 891 shows polarized synchrotron radiation up to 4 kpc into the halo, in which the field ordering first increases, then decreases with z (Hummel et a1 1991). Another edge-on galaxy, NGC 4631 shows a similar behavior (Hummel et a1 1988, 1991), but with a radially aligned magnetic field direction (the sense is not measured) out to 7 kpc from the disk - see figure 7 (section 3.1 below). For the same galaxy, another scale height has been measured, namely that of the ionized gas layer by imaging the diffuse optical H emission, giving a scale height of 1.1 kpc (Rand et al 1990, Dettmar 1990). The H data agree with a similar scale height of 0.9 kpc estimated from Faraday dispersion due to thermal ionized gas embedded within the polarized halo emission (Hummel et a1 1991).