


2.3. The physics of magnetic field amplification and evolution in spiral galaxies
2.3.1. The fundamental processes. The equations governing the evolution of magnetic field in non-viscous conducting plasma consist of Maxwell's equations, Ohm's law, the equation of continuity, and an equation of motion:
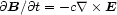 |
(2.1) |
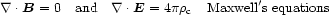 |
(2.2) |
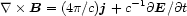 |
(2.3) |
 |
(2.4) |
 |
(2.5) |
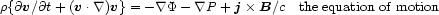 |
(2.6) |
The electric and magnetic fields are E and
B, respectively,
 is the mass
density, j is the current density,
is the mass
density, j is the current density,
 is the conductivity,
is the conductivity,
 c is the
net charge density, P the pressure,
v the velocity, and
c is the
net charge density, P the pressure,
v the velocity, and
 is the gravitational
potential. We note in passing that P includes
the interstellar thermal gas and cosmic ray pressures, including
that of the (sometimes ignored) relativistic protons and heavier
nuclei. These particles may have
is the gravitational
potential. We note in passing that P includes
the interstellar thermal gas and cosmic ray pressures, including
that of the (sometimes ignored) relativistic protons and heavier
nuclei. These particles may have
 102 times
the energy of the `visible' synchrotron-emitting relativistic
electrons. The evolution of the magnetic field is described by solutions
to the induction equation (cf
Parker 1979),
which can be derived from equations (2.1), (2.3) and (2.4)
102 times
the energy of the `visible' synchrotron-emitting relativistic
electrons. The evolution of the magnetic field is described by solutions
to the induction equation (cf
Parker 1979),
which can be derived from equations (2.1), (2.3) and (2.4)
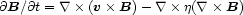 |
(2.7) |
where  =
c2 / 4
=
c2 / 4
 is the magnetic
diffusivity. If the magnetic field is `frozen in', then
is the magnetic
diffusivity. If the magnetic field is `frozen in', then
 = 0 (or
= 0 (or
 =
=
 ), so that the term
), so that the term
 ×
×
 (
( × B)
vanishes. Another relevant quantity is the magnetic Reynolds number,
× B)
vanishes. Another relevant quantity is the magnetic Reynolds number,
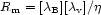 |
(2.8) |
where
[ B] and
[
B] and
[ v] are the
typical variation scales for B and
v, respectively. For most purposes in this review, the regime
Rm >> 1 applies. In the
absence of pressure and density perturbations, MHD waves will propagate
with the Alfvén velocity which is given by
v] are the
typical variation scales for B and
v, respectively. For most purposes in this review, the regime
Rm >> 1 applies. In the
absence of pressure and density perturbations, MHD waves will propagate
with the Alfvén velocity which is given by
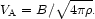 |
(2.9) |
For a more complete discussion of physical processes in magnetoplasmas the reader is referred to Parker (1979), Zel'dovich et al (l983), Priest (1985), Asseo and Sol (1987) and references therein. It is important to note that equation (2.7) does not contain a source term for magnetic field. This underlines the need for theories to account for the source of magnetic fields - such as the Biermann battery mechanism, or a cosmological seed field (cf section 5). Thus a pre-existing 'seed' field is presupposed. The second important point is that even after a source, or seed field is identified, a generation process is required to sustain the fields against resistive and other decay processes - represented by the second term in equation (2.7).
The gravitationally-driven dynamics of disk galaxies naturally provide a large scale, ordered motion with a large energy density. The following section describes the 'conventional' galactic dynamo mechanism, which is based on concepts developed earlier for the Sun and Earth (Parker 1955, Steenbeck et al 1966, Steenbeck and Krause 1969, and others). It attempts to describe how ordered galactic motions can amplify, and at the same time produce ordered magnetic fields, which 'tap into' the larger source of gravitational energy in large spiral galaxies. It assumes that the initial fields were very much weaker than at the present epoch - an assumption which we shall later call into question. It also largely ignores the role of cosmic rays, an aspect which we also discuss later.
2.3.2. The conventional galactic dynamo in
'well-behaved' disk galaxies.
Spiral disk galaxies possess gravitationally driven ordered
motions, namely a 'solid body'
(v
 r)
rotation which, due to the galaxy's distributed mass, transforms into
differential rotation at larger galactocentric radii. The latter may or
may not be quasi-Keplerian (depending on the global distribution of
mass), but in any case there is velocity shear
(
r)
rotation which, due to the galaxy's distributed mass, transforms into
differential rotation at larger galactocentric radii. The latter may or
may not be quasi-Keplerian (depending on the global distribution of
mass), but in any case there is velocity shear
( v /
v /
 r).
Superimposed on these global dynamics are streaming motions, possibly
induced by density waves and/or magnetic fields (see below) and, for
some galaxies, non-axisymmetric motions due to gravitational
interactions with satellite or other nearby galaxies. Finally there are
interstellar turbulent motions, typically a few km s-1. Typical
(kinetic) energy densities due to global rotation,
r).
Superimposed on these global dynamics are streaming motions, possibly
induced by density waves and/or magnetic fields (see below) and, for
some galaxies, non-axisymmetric motions due to gravitational
interactions with satellite or other nearby galaxies. Finally there are
interstellar turbulent motions, typically a few km s-1. Typical
(kinetic) energy densities due to global rotation,
 grav,
are of order 3.3 × 10-10 erg cm-3,
but these decrease significantly at large galactocentric radii. By
contrast, energy densities of the synchrotron-emitting cosmic ray gas
grav,
are of order 3.3 × 10-10 erg cm-3,
but these decrease significantly at large galactocentric radii. By
contrast, energy densities of the synchrotron-emitting cosmic ray gas
 cr
are of order 10-12 erg cm-3 and the
interstellar magnetic energy density is
cr
are of order 10-12 erg cm-3 and the
interstellar magnetic energy density is
 m
= ((B / 5µ G)2 × 10-12 erg
cm-3. The energy density of the smaller-scale turbulent motions,
m
= ((B / 5µ G)2 × 10-12 erg
cm-3. The energy density of the smaller-scale turbulent motions,
 t
= 1/2
t
= 1/2  v2, is
v2, is
 0.6 ×
10-12 erg cm-3. Of
fundamental significance for the physics of large scale MHD processes in
galaxies are the facts just illustrated, that
0.6 ×
10-12 erg cm-3. Of
fundamental significance for the physics of large scale MHD processes in
galaxies are the facts just illustrated, that
 grav
dominates the others (except at large galactocentric radii), and that
grav
dominates the others (except at large galactocentric radii), and that
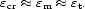 |
(2.10) |
We can further note that the
 V of
density wave-induced streaming motions are of order 5-10 km
s-1, so that
V of
density wave-induced streaming motions are of order 5-10 km
s-1, so that

 grav
grav
 3 ×
10-13 erg cm-3, is not much different from
3 ×
10-13 erg cm-3, is not much different from
 cr,
cr,
 m
and
m
and  t.
Another important energy component to consider
is that due to supernovae (or multiple supernovae within a small
galactic region) and dense clusters of young stars,
both of which can, temporarily and locally, deposit significant energy
densities (in the form of
t.
Another important energy component to consider
is that due to supernovae (or multiple supernovae within a small
galactic region) and dense clusters of young stars,
both of which can, temporarily and locally, deposit significant energy
densities (in the form of
 cr,
cr,
 m and
m and
 t)
into the otherwise 'quiescent' interstellar disk. We
shall call this component
t)
into the otherwise 'quiescent' interstellar disk. We
shall call this component  * . These basic energetic
facts are key to the evolution of magnetic fields in galaxy disks.
* . These basic energetic
facts are key to the evolution of magnetic fields in galaxy disks.
An elegant theory for field amplification called the
 -
-
 dynamo was originally applied to solar magnetic fields
(Steenbeck and Krause
1969),
and was worked out in the 1960s for galactic magnetic fields by
Stix (1975),
White (1978),
Parker (1966,
1971)
and Vainstein and
Ruzmaikin (1971).
The theory makes use of what is called the mean field approximation
(cf Krause and
Rädler 1980)
which is needed to accommodate the
fact that we are dealing with averages over a range of correlation
scales <li> and times
<ti> of the velocity field, and fluctuations in the
magnetic field <Bi>. Proof of the
validity of the mean field approximation, although not trivial, has been
worked out
(Krause and Rädler
1980,
Zel'dovich et al 1983;
cf also
van Kampen 1974,
Knobloch 1978);
it is, roughly speaking, an MHD analogue of statistical mechanical
methods in the study of gases. However the validity of the mean-field
solutions has been questioned by
Kulsrud and Anderson
(1992)
who calculate that the build-up of fluctuation energy
on small scales occurs before the mean field has a chance to be
amplified (see section 2.3.5 below for a related
discussion). This
latter question should eventually be resolvable through ISM magnetic
field measurements over the appropriate range of scales. The tentative
result is that the magnetic fluctuation energy does not appear to
increase at
smaller scales. In fluid mechanics the energy density-wavenumber (k)
distribution follows a Kolmogorov spectrum, whose logarithmic slope is
-5/3 up to some maximum k,
where viscosity effect take over and cause a small-scale (high k)
cut-off. By contrast, in magnetohydrodynamic theory there appears to be
no analogously definitive exponent which can confidently specify the
variation of magnetic field strength with fluctuation scale. In a
stratified, rotating and turbulent (or convective) section of the galaxy
disk, the first induction action, which is due to the velocity shear,
d
dynamo was originally applied to solar magnetic fields
(Steenbeck and Krause
1969),
and was worked out in the 1960s for galactic magnetic fields by
Stix (1975),
White (1978),
Parker (1966,
1971)
and Vainstein and
Ruzmaikin (1971).
The theory makes use of what is called the mean field approximation
(cf Krause and
Rädler 1980)
which is needed to accommodate the
fact that we are dealing with averages over a range of correlation
scales <li> and times
<ti> of the velocity field, and fluctuations in the
magnetic field <Bi>. Proof of the
validity of the mean field approximation, although not trivial, has been
worked out
(Krause and Rädler
1980,
Zel'dovich et al 1983;
cf also
van Kampen 1974,
Knobloch 1978);
it is, roughly speaking, an MHD analogue of statistical mechanical
methods in the study of gases. However the validity of the mean-field
solutions has been questioned by
Kulsrud and Anderson
(1992)
who calculate that the build-up of fluctuation energy
on small scales occurs before the mean field has a chance to be
amplified (see section 2.3.5 below for a related
discussion). This
latter question should eventually be resolvable through ISM magnetic
field measurements over the appropriate range of scales. The tentative
result is that the magnetic fluctuation energy does not appear to
increase at
smaller scales. In fluid mechanics the energy density-wavenumber (k)
distribution follows a Kolmogorov spectrum, whose logarithmic slope is
-5/3 up to some maximum k,
where viscosity effect take over and cause a small-scale (high k)
cut-off. By contrast, in magnetohydrodynamic theory there appears to be
no analogously definitive exponent which can confidently specify the
variation of magnetic field strength with fluctuation scale. In a
stratified, rotating and turbulent (or convective) section of the galaxy
disk, the first induction action, which is due to the velocity shear,
d /
dr, causes an azimuthal field,
B
/
dr, causes an azimuthal field,
B , if there is initially a radial field,
Br,
(Krause 1987).
If we approximate the galaxy disk as a flattened, oblate spheroid of
scale b along the rotation (z-) axis,
and whose radial scale is a, we can, following
Krause (1987),
define an
, if there is initially a radial field,
Br,
(Krause 1987).
If we approximate the galaxy disk as a flattened, oblate spheroid of
scale b along the rotation (z-) axis,
and whose radial scale is a, we can, following
Krause (1987),
define an  parameter
parameter
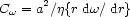 |
(2.11) |
where r is the radial coordinate. We now consider an additional
effect
when turbulence is introduced into this stratified, magnetized layer:
turbulent motion will be subject to the Coriolis force in this
rotating system. Thus, for example, as a bubble of gas expands out of
the plane, it will create an expanding `loop' which, due to its
Bz component (see figure 4)
will be twisted by the Coriolis force as it moves out of the
plane; in the right-handed sense above the plane (if
 is directed
upwards as in figure 4), and in the opposite
sense below the plane,
thus introducing an natural helicity to the outflowing
magneto-plasma. This gives rise to the so-called
is directed
upwards as in figure 4), and in the opposite
sense below the plane,
thus introducing an natural helicity to the outflowing
magneto-plasma. This gives rise to the so-called
 -effect. Note that
the moving Bz component will induce a current which is
antiparallel to
B
-effect. Note that
the moving Bz component will induce a current which is
antiparallel to
B (see also below).
(see also below).
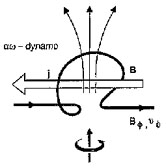 |
Figure 4. Illustration of the
|
Another natural consequence of the
 -effect is the
production of a
poloidal magnetic field component. Because the energy density of the
rotational motion is normally higher than
-effect is the
production of a
poloidal magnetic field component. Because the energy density of the
rotational motion is normally higher than
 t in a
well behaved spiral
galaxy, the repeated twisting and stretching effects can amplify the
field in the disk. In mean-field electrodynamics,
t in a
well behaved spiral
galaxy, the repeated twisting and stretching effects can amplify the
field in the disk. In mean-field electrodynamics,
 , related to the
helicity, <v .
(
, related to the
helicity, <v .
( .
v)>, is defined as
.
v)>, is defined as
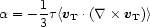 |
(2.12) |
where  is the correlation
time of the turbulent velocity field represented by
vT. The characteristic
is the correlation
time of the turbulent velocity field represented by
vT. The characteristic
 -parameter (again following
Krause 1987) is
-parameter (again following
Krause 1987) is
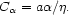 |
(2.13) |
We are now in a position to evaluate these parameters for the disk of a
spiral galaxy, such as the Milky Way. The rotational shear,
r d / dr
(Oort's constant) near the Sun is -30 kpc km s-1,
vT is
/ dr
(Oort's constant) near the Sun is -30 kpc km s-1,
vT is
 10 km
s-1, a
10 km
s-1, a
 15 kpc. The size of
the turbulent elements,
15 kpc. The size of
the turbulent elements, 
 100 pc. The lifetime
of the turbulent elements,
100 pc. The lifetime
of the turbulent elements,  ,
the only non-measurable, can be reasonably estimated from
,
the only non-measurable, can be reasonably estimated from
 / v
/ v
 3 ×
1014 s (= 107 yr). A key point is that, specifically
due to the Coriolis force, the average
<vT .
(
3 ×
1014 s (= 107 yr). A key point is that, specifically
due to the Coriolis force, the average
<vT .
( ×
vT)< is
non-zero, so that when we incorporate
×
vT)< is
non-zero, so that when we incorporate
 into the field
regeneration equation (2.7), we see that the
into the field
regeneration equation (2.7), we see that the
 -term will
affect the growth of the magnetic field. The helicity can be
expressed as
-term will
affect the growth of the magnetic field. The helicity can be
expressed as
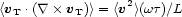 |
(2.14) |
(Krause 1987)
where L( 
 ) is the scale height,
a value for which can be taken from
Simard-Normandin and
Kronberg's (1980)
estimate of the magneto-ionic thickness of
the Milky Way's disk in the vicinity of the Sun
(section 2.2.3).
) is the scale height,
a value for which can be taken from
Simard-Normandin and
Kronberg's (1980)
estimate of the magneto-ionic thickness of
the Milky Way's disk in the vicinity of the Sun
(section 2.2.3).
To illustrate how a differentially rotating galaxy disk can amplify a
pre-existing magnetic field, we re-write equation (2.7) now
incorporating  :
:
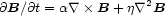 |
(2.15) |
where  and
and
 are taken as
constants (up to this point). A typical galactic value for
the magnetic diffusivity is
are taken as
constants (up to this point). A typical galactic value for
the magnetic diffusivity is

 0.1
0.1 v,
v,
 1025
cm2 s-1 .
1025
cm2 s-1 .
2.3.3. Solutions to the mean field dynamo regeneration equation in the linear regime. Solutions to (2.15) can be written in the form
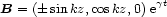 |
(2.16) |
where  =
-
=
-  k2 ±
k2 ±
 k, k being
the wavenumber
(Zel'dovich et al
1983).
|B| grows exponentially with time for non-zero
helicity, positive or negative, and if the scales are sufficiently large
(k < |
k, k being
the wavenumber
(Zel'dovich et al
1983).
|B| grows exponentially with time for non-zero
helicity, positive or negative, and if the scales are sufficiently large
(k < | |
|
 ). Another
consequence of equation (2.15) is that a mean electric field, hence a
mean current, will be directed along the magnetic field
(Moffatt 1978,
Krause and Rädler
1980)
as illustrated in figure 4. The mean field
generation
equation should be regarded as an approximation of a complex MHD problem
in 3D , and there are several simplifying assumptions implicit in our
summary discussion here. Our purpose here is limited to illustrating the
fundamental physical processes, and to showing how the solutions indeed
provide a first-order confirmation of the observed
geometry of magnetic fields in disk galaxies, and possibly their
present-day strengths. Later in
sections 2.3.4 and 2.3.5, we
shall cast doubt on whether the standard, mean field dynamo can actually
work in many galaxies.
). Another
consequence of equation (2.15) is that a mean electric field, hence a
mean current, will be directed along the magnetic field
(Moffatt 1978,
Krause and Rädler
1980)
as illustrated in figure 4. The mean field
generation
equation should be regarded as an approximation of a complex MHD problem
in 3D , and there are several simplifying assumptions implicit in our
summary discussion here. Our purpose here is limited to illustrating the
fundamental physical processes, and to showing how the solutions indeed
provide a first-order confirmation of the observed
geometry of magnetic fields in disk galaxies, and possibly their
present-day strengths. Later in
sections 2.3.4 and 2.3.5, we
shall cast doubt on whether the standard, mean field dynamo can actually
work in many galaxies.
A requirement of (2.15) and (2.16) is that characteristic field growth
times be longer than 5. Other restrictive statements we have made above
must be modified under different (but still reasonable!)
assumptions. For example, our statement above that connects the mean
helicity with the  parameter is subject to the assumption that the turbulence associated with
parameter is subject to the assumption that the turbulence associated with
 is isotropic. In
reality, because of stratification, gravity, and rotational motion in galaxy
disks,
is isotropic. In
reality, because of stratification, gravity, and rotational motion in galaxy
disks,  is generally a
tensor (cf
Krause and Rädler
1980,
1986,
Elstner et al (1992).
As Zel'dovich et al
(1983)
point out, mean field generation, i.e. solutions of the form
|B|
is generally a
tensor (cf
Krause and Rädler
1980,
1986,
Elstner et al (1992).
As Zel'dovich et al
(1983)
point out, mean field generation, i.e. solutions of the form
|B|  e
e t
(Re
t
(Re  > 0)
are also possible if the turbulence is homogeneous and
anisotropic. For the purpose of this review, this latter fact
serves to underline the relative robustness (though not unchallenged) of
the mean field solutions as they apply to disk galaxies. The reader is
referred to
Zel'dovich et al (1983)
for a lucid physical treatment of kinematic turbulent dynamos, and their
application to galactic magnetic fields.
> 0)
are also possible if the turbulence is homogeneous and
anisotropic. For the purpose of this review, this latter fact
serves to underline the relative robustness (though not unchallenged) of
the mean field solutions as they apply to disk galaxies. The reader is
referred to
Zel'dovich et al (1983)
for a lucid physical treatment of kinematic turbulent dynamos, and their
application to galactic magnetic fields.
To create an expected `model' field distribution, it is instructive to
parameterize the  and
and
 effects separately, and
then establish, for
typical disk galaxy conditions, which modes dominate in what part of the
galaxy. The numerical values of the
effects separately, and
then establish, for
typical disk galaxy conditions, which modes dominate in what part of the
galaxy. The numerical values of the
 and
and
 parameters (2.1 1 and 2.13), from the observationally estimated values
in (2.3.2) above
are: C
parameters (2.1 1 and 2.13), from the observationally estimated values
in (2.3.2) above
are: C
 - 7000 (the minus
sign from the negative d
- 7000 (the minus
sign from the negative d  / d r), and
C
/ d r), and
C
 50
50
 / L. It is
immediately evident that
|C
/ L. It is
immediately evident that
|C |
/ C
|
/ C >> 1, meaning that the dominant
induction action for the amplification of the azimuthal (toroidal) field
in the disk is differential rotation (cf
Krause 1987).
Another useful parameter is C1 =
C
>> 1, meaning that the dominant
induction action for the amplification of the azimuthal (toroidal) field
in the disk is differential rotation (cf
Krause 1987).
Another useful parameter is C1 =
C C
C
 10-5 for
the Milky Way. The
C-parameters are convenient for exploring the solutions for model
galaxy disks, which were first obtained by
Stix (1975).
The general result for the
10-5 for
the Milky Way. The
C-parameters are convenient for exploring the solutions for model
galaxy disks, which were first obtained by
Stix (1975).
The general result for the
 -
-
 dynamo is illustrated
in figure 5 : The azimuthal field distribution
is shown on the
right-hand side of this composite flat-ellipse model, and the left side
illustrates that a poloidal component,
which has a quadrupole geometry in 3D, is also produced by the
dynamo is illustrated
in figure 5 : The azimuthal field distribution
is shown on the
right-hand side of this composite flat-ellipse model, and the left side
illustrates that a poloidal component,
which has a quadrupole geometry in 3D, is also produced by the
 -
-
 dynamo.
dynamo.
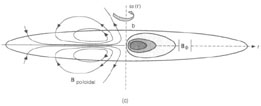 |
Figure 5. The 3D magnetic field
configuration produced by the
|
The B solution shown in figure 5 is
axisymmetric with respect to the
galaxy's rotation axis, and it has reflection symmetry about the
equatorial plane. Other solution modes are possible, and testable
against observations, especially those of the Faraday RM
distribution. Other eigensolutions of the regeneration equation can also
produce field geometries which are antisymmetric about the equator
(cf Krause 1987),
and other azimuthal modes. In particular, the azimuth dependence of
B is modulated by
eim where
m = 0 and m = 1 give axisymmetric and bisymmetric field
distributions, respectively, as illustrated in
figure 3. Two nearby
galaxies (M81 and M51) appear to have an m = 1
mode azimuthal field distribution (cf
Krause et al 1989,
Tosa and Fujimoto
1978,
Horellou et a1 1990
and figure 3(c)), while some
other others, e.g.
NGC 6946, appear
consistent with an m = 0 mode for the global field, at
least at low angular resolution.
This is indeed the solution mode for the mean-field
where
m = 0 and m = 1 give axisymmetric and bisymmetric field
distributions, respectively, as illustrated in
figure 3. Two nearby
galaxies (M81 and M51) appear to have an m = 1
mode azimuthal field distribution (cf
Krause et al 1989,
Tosa and Fujimoto
1978,
Horellou et a1 1990
and figure 3(c)), while some
other others, e.g.
NGC 6946, appear
consistent with an m = 0 mode for the global field, at
least at low angular resolution.
This is indeed the solution mode for the mean-field
 -
-
 dynamo with the highest growth rate, for the linear regime and with no
distortions from axisymmetry (cf also
Elstner et al 1992
for relevant numerical simulations). We note, however, that B-field
maps from the radio data with the highest linear resolution (in kpc)
suggest that reality may not be as simple as just indicated
(section 2.2.2). A final judgement on the
morphology of magnetic orientation
and sign should await higher resolution images. So far, the highest
resolution comes from the optical B-images but, as noted earlier,
they are insensitive to the field sign.
dynamo with the highest growth rate, for the linear regime and with no
distortions from axisymmetry (cf also
Elstner et al 1992
for relevant numerical simulations). We note, however, that B-field
maps from the radio data with the highest linear resolution (in kpc)
suggest that reality may not be as simple as just indicated
(section 2.2.2). A final judgement on the
morphology of magnetic orientation
and sign should await higher resolution images. So far, the highest
resolution comes from the optical B-images but, as noted earlier,
they are insensitive to the field sign.
Stimulated by the apparent existence of a dominant m = 1 mode in at
least some galaxies (see section 2.2.2 above),
several workers have
explored the appropriate model parameter space for stable bisymmetric
disk field solutions to the dynamo equations.
Fujimoto and Sawa (1987,
1990) and
Chiba and Tosa (1990)
have produced numerical
simulations showing this to be favored for thick magneto-ionic disk layers
(zm
 0.5 kpc) and
larger turbulent velocities which persist away from the disk. Solutions
exist which give a quasi-rigid rotation,
0.5 kpc) and
larger turbulent velocities which persist away from the disk. Solutions
exist which give a quasi-rigid rotation,
 BSS, which is
close to that for spiral density wave pattern,
BSS, which is
close to that for spiral density wave pattern,
 DW. This
makes it possible, even likely,
for a resonant coupling to be set up between the two phenomena
(Fujimoto and Sawa 1990,
Tosa and Chiba 1990,
Chiba and Tosa 1990).
We recall (section 2.3.2) that the energy
associated with the
density wave-driven velocity perturbations is comparable to that in the
magnetic field perturbations. Such an effect has at least two
interesting implications for galaxy evolution: (i) large scale
bisymmetric field amplification could, in the right circumstances, be
enhanced by density wave patterns and vice versa, and (ii) the
diffusion times of density waves,
DW. This
makes it possible, even likely,
for a resonant coupling to be set up between the two phenomena
(Fujimoto and Sawa 1990,
Tosa and Chiba 1990,
Chiba and Tosa 1990).
We recall (section 2.3.2) that the energy
associated with the
density wave-driven velocity perturbations is comparable to that in the
magnetic field perturbations. Such an effect has at least two
interesting implications for galaxy evolution: (i) large scale
bisymmetric field amplification could, in the right circumstances, be
enhanced by density wave patterns and vice versa, and (ii) the
diffusion times of density waves,
 109 yr
(Toomre 1969),
might be substantially modified, in particular, lengthened by
magnetic reinforcement (see below).
109 yr
(Toomre 1969),
might be substantially modified, in particular, lengthened by
magnetic reinforcement (see below).
Moss and Tuominen
(1990)
investigate solutions for 'thick disk' models in the non-linear
regime (caused by an
' -quenching' mechanism
- see also
Brandenburg et al 1989).
They conclude that long term oscillations are possible between solution
modes, in which bisymmetric and axisymmetric field geometries alternate
over a galaxy's lifetime. They also find that the final mode, whether
stationary or oscillatory, could depend
on the initial conditions. The possibility of such non-linear,
'transient' phenomena has emerged largely as the result of increasing
experience with non-linear galactic dynamo models. In particular
Brandenburg et al
(1992) and
Poezd et al (1993),
suggest that non-axisymmetric field patterns, including large scale
field reversals in galaxy disks, are possibly transient phenomena,
rather than stable solutions. This possibility, at least for
the time being, complicates the interpretation of the early magnetic
history of galaxies. Unlike with the Sun, we are not permitted the
luxury of observing the time evolution of large scale galactic magnetic
features!
-quenching' mechanism
- see also
Brandenburg et al 1989).
They conclude that long term oscillations are possible between solution
modes, in which bisymmetric and axisymmetric field geometries alternate
over a galaxy's lifetime. They also find that the final mode, whether
stationary or oscillatory, could depend
on the initial conditions. The possibility of such non-linear,
'transient' phenomena has emerged largely as the result of increasing
experience with non-linear galactic dynamo models. In particular
Brandenburg et al
(1992) and
Poezd et al (1993),
suggest that non-axisymmetric field patterns, including large scale
field reversals in galaxy disks, are possibly transient phenomena,
rather than stable solutions. This possibility, at least for
the time being, complicates the interpretation of the early magnetic
history of galaxies. Unlike with the Sun, we are not permitted the
luxury of observing the time evolution of large scale galactic magnetic
features!
An ingenious scenario to explain stable, non-axisymmetric fields has
been proposed by
Mestel
and Subramanian (1991).
They consider the two-arm spiral - the type most
clearly observed to have a bisymmetric field pattern - which has been
traditionally believed to be density wave-driven. They make the
physically plausible assumption that the
 parameter is
azimuth-dependent, and that it follows the spiral pattern imposed
by the density wave. They obtain rapidly growing bisymmetric fields
which corotate with the spiral pattern, in approximate agreement with
the results of
Fujimoto and Sawa
(1990).
Further, Mestel and
Subramanian (1991)
invoke independent arguments
(Nakano 1984,
Campbell and Mestel
1987)
that a stronger field will bias the stellar mass
spectrum, favoring the formation of more massive stars. The associated
expanding H II regions/supernova remnants and planetary nebulae will
then increase the turbulence, and hence quite likely the helicity
(through interaction with the galactic rotation). This,
in turn would further enhance the non-axisymmetric
parameter is
azimuth-dependent, and that it follows the spiral pattern imposed
by the density wave. They obtain rapidly growing bisymmetric fields
which corotate with the spiral pattern, in approximate agreement with
the results of
Fujimoto and Sawa
(1990).
Further, Mestel and
Subramanian (1991)
invoke independent arguments
(Nakano 1984,
Campbell and Mestel
1987)
that a stronger field will bias the stellar mass
spectrum, favoring the formation of more massive stars. The associated
expanding H II regions/supernova remnants and planetary nebulae will
then increase the turbulence, and hence quite likely the helicity
(through interaction with the galactic rotation). This,
in turn would further enhance the non-axisymmetric
 -distribution
which is capable of reinforcing the dynamo which produced the bisymmetric
field. This is a new idea, in
which the field acts as a type of `catalyst', which increases energy
input into the interstellar turbulence. If true, Mestel and
Subramanian's mechanism would make it much
more natural for the spiral structure to be at least partially
magnetically influenced with the currently estimated field strengths, in
contrast to previous thinking in this subject (see e.g.
Binney and Tremaine
1987).
-distribution
which is capable of reinforcing the dynamo which produced the bisymmetric
field. This is a new idea, in
which the field acts as a type of `catalyst', which increases energy
input into the interstellar turbulence. If true, Mestel and
Subramanian's mechanism would make it much
more natural for the spiral structure to be at least partially
magnetically influenced with the currently estimated field strengths, in
contrast to previous thinking in this subject (see e.g.
Binney and Tremaine
1987).
Initial conditions resulting from mergers, or earlier tidal encounters
clearly would violate the assumption of initial axisymmetry inherent in
the models discussed above, and have thus far not been explored in
detail (see also section 5.5.1).
The general
conclusion from the above is that departures from axisymmetry, which are
strongly indicated in some galaxies, can be reproduced as either
transient or permanent solutions to the mean field
 -
-
 dynamo regeneration
equations.
Lesch (1993)
has emphasized the importance of the intrastellar gas, in contrast
to the stellar component, in the excitation of non-axisymmetric
instabilities in galaxies. His numerical model calculations produce
significantly shorter field amplification times when the dynamo action
is driven by non-axisymmetric features (e.g. strong bars, and some tidal
interaction effects), than for an axisymmetric dynamo.
dynamo regeneration
equations.
Lesch (1993)
has emphasized the importance of the intrastellar gas, in contrast
to the stellar component, in the excitation of non-axisymmetric
instabilities in galaxies. His numerical model calculations produce
significantly shorter field amplification times when the dynamo action
is driven by non-axisymmetric features (e.g. strong bars, and some tidal
interaction effects), than for an axisymmetric dynamo.
A further important point emphasized by
Krause and Meinel
(1988)
is that, as long as
C ,
(equation (2.13)) exceeds the critical
value for field growth, the relative sizes of
the linear growth rates may be unimportant in deciding what the final
field configurations will be. Saturation effects, and non-linear effects
due to back-reactions can erase a galaxy's memory of the relative growth
rates of different field amplification modes.
,
(equation (2.13)) exceeds the critical
value for field growth, the relative sizes of
the linear growth rates may be unimportant in deciding what the final
field configurations will be. Saturation effects, and non-linear effects
due to back-reactions can erase a galaxy's memory of the relative growth
rates of different field amplification modes.
2.3.4. The dynamo effect for inner galactic rotation
zones (the  2-dynamo). In the
nuclear regions, the magnetic field should have a poloidal geometry
according to the standard dynamo model (cf
figure 5). Unfortunately it
is difficult to observationally
isolate the morphology of the magnetic fields in and above the
d
2-dynamo). In the
nuclear regions, the magnetic field should have a poloidal geometry
according to the standard dynamo model (cf
figure 5). Unfortunately it
is difficult to observationally
isolate the morphology of the magnetic fields in and above the
d / d r
/ d r
 0 zone from
the disks onto which they are normally seen projected.
0 zone from
the disks onto which they are normally seen projected.
In the inner galactic zones, which are interior to most of the galaxy's
mass, and  is
independent of galactocentric radius
(d
is
independent of galactocentric radius
(d / d r
/ d r
 0), the parameter
C
0), the parameter
C is
much smaller than in the outer galaxy disk. Hence the conditions for the
amplification of disk fields no longer apply. However, the current
generated by the helicity
(
is
much smaller than in the outer galaxy disk. Hence the conditions for the
amplification of disk fields no longer apply. However, the current
generated by the helicity
( -effect) just outside
where d
-effect) just outside
where d / d r becomes
non-zero, generates a poloidal field component. In addition,
because the inner rotating and conducting gas has some helicity
(
/ d r becomes
non-zero, generates a poloidal field component. In addition,
because the inner rotating and conducting gas has some helicity
(
 0), it causes a
poloidal current, which reinforces the toroidal magnetic field. In turn,
this toroidal magnetic field drives a toroidal current, which reinforces
the poloidal magnetic field (cf
Krause 1987).
This is the
0), it causes a
poloidal current, which reinforces the toroidal magnetic field. In turn,
this toroidal magnetic field drives a toroidal current, which reinforces
the poloidal magnetic field (cf
Krause 1987).
This is the  2
dynamo effect, which (a) stabilizes and/or
amplifies the poloidal field component (Bz) in the inner
(d
2
dynamo effect, which (a) stabilizes and/or
amplifies the poloidal field component (Bz) in the inner
(d / d r
/ d r
 0) region of the
galaxy, and (b) provides a natural coupling to the predominantly
azimuthal field in the outer,
d
0) region of the
galaxy, and (b) provides a natural coupling to the predominantly
azimuthal field in the outer,
d / d r <
0 disk, which is due to the
/ d r <
0 disk, which is due to the
 -
-
 dynamo described
earlier. All of this assumes
the absence of large scale outflow winds from the inner galactic zones.
dynamo described
earlier. All of this assumes
the absence of large scale outflow winds from the inner galactic zones.
2.3.5. The current state of comprehensive (disk +
halo) dynamo-generated field morphologies in 'normal' spiral
galaxies.
A more complete model of a dynamo-regenerated
magnetic field must include the halo, for which
Sokoloff and Shukurov
(1990)
have proposed a mean-field dynamo model. In their model, the dynamo field
growth times are of the order of, or greater than a typical galaxy's
lifetime, so that some memory of the hypothesized primordial field could
be discernible, given detailed observations of Faraday rotation in the
halo. Unfortunately the latter are difficult to obtain, even in a 2D
projection for a galaxy see11 edge-on. This is partly because of the
loss of the third geometrical dimension in a system where axisymmetry
cannot be assumed, and indeed may contain a quadrupolar mode (cf
figure 5). Additionally, as emphasized by
Sukumar and Allen
(1991)
in their study of NGC 891 and NGC 4565, significant Faraday
dispersion effects at decimeter
 s - just where the
polarized synchrotron radiation is most readily detectable - `erases'
information about the magnetic field geometry at the
rear parts of the halo, which is difficult, if not impossible to
reconstruct. Theoretical modeling has been extended to combined halo
+ disk numerical simulation model calculations by
Brandenburg et al
(1992),
in which the halo possesses strong turbulent diffusivity, and an
s - just where the
polarized synchrotron radiation is most readily detectable - `erases'
information about the magnetic field geometry at the
rear parts of the halo, which is difficult, if not impossible to
reconstruct. Theoretical modeling has been extended to combined halo
+ disk numerical simulation model calculations by
Brandenburg et al
(1992),
in which the halo possesses strong turbulent diffusivity, and an
 halo
halo
 10 ×
10 ×
 disk. Initial
axisymmetry is preserved throughout in their
calculations, and galactic winds are assumed to be small
(
disk. Initial
axisymmetry is preserved throughout in their
calculations, and galactic winds are assumed to be small
( 50 km
s-1, so that the field
is not advected away into the IGM and thereby `spoiling' the dynamo
effect (see, however, below). The results of these, and the recent
simulations of
Elstner et al (1992)
show
that even with these simplifying assumptions, quite complex galactic
field structures can emerge from the numerical solutions.
Brandenburg et a1 (1993)
have more recently extended their numerical models, concentrating on
halos, and introducing galactic winds and departures from isotropy in
50 km
s-1, so that the field
is not advected away into the IGM and thereby `spoiling' the dynamo
effect (see, however, below). The results of these, and the recent
simulations of
Elstner et al (1992)
show
that even with these simplifying assumptions, quite complex galactic
field structures can emerge from the numerical solutions.
Brandenburg et a1 (1993)
have more recently extended their numerical models, concentrating on
halos, and introducing galactic winds and departures from isotropy in
 . They have succeeded in
obtaining solutions which
give broad agreement with the 2D halo field maps of NGC 891 (which has a
weak wind), and NGC 4631 (figure 7) which has a stronger wind and a
striking, quasi-radial halo magnetic field geometry.
. They have succeeded in
obtaining solutions which
give broad agreement with the 2D halo field maps of NGC 891 (which has a
weak wind), and NGC 4631 (figure 7) which has a stronger wind and a
striking, quasi-radial halo magnetic field geometry.
Parker (1992)
has pointed out that, although the observation-based estimates of the
physical parameters in section 2.3.2 give mean
field solutions which
appear to agree with observations, one key parameter, the turbulent
diffusivity  ,
needs careful physical justification (cf also
Rosner and DeLuca
1989).
Standard dynamo theory, as reviewed
above, prescribes random kinematic swirling and mixing in order to
explain the turbulent eddy diffusion,
,
needs careful physical justification (cf also
Rosner and DeLuca
1989).
Standard dynamo theory, as reviewed
above, prescribes random kinematic swirling and mixing in order to
explain the turbulent eddy diffusion,
 t
t
 1025
cm2 s-1
(Parker 1955,
1970,
1979,
Steenbeck et al 1966,
Vainstein and Zel'dovich
1972).
This model is based on both global and local kinematics, and assumes
that the field is mixed and filamented down to scales of order 0.1 au.
This smallest size is roughly the mixing scale which is required in
order that molecular
resistivity can provide the required dissipation of large scale fields
in
1025
cm2 s-1
(Parker 1955,
1970,
1979,
Steenbeck et al 1966,
Vainstein and Zel'dovich
1972).
This model is based on both global and local kinematics, and assumes
that the field is mixed and filamented down to scales of order 0.1 au.
This smallest size is roughly the mixing scale which is required in
order that molecular
resistivity can provide the required dissipation of large scale fields
in  108 yr;
i.e. that required to provide a large enough value of
108 yr;
i.e. that required to provide a large enough value of
 so that the field
regeneration according to equation (2.15) will actually work. As
Parker (1992)
has emphasized, there is no known way, with
<B> as strong as several µG and
|
so that the field
regeneration according to equation (2.15) will actually work. As
Parker (1992)
has emphasized, there is no known way, with
<B> as strong as several µG and
| B|
(
B|
( <B>) fluctuating on a scale
of
<B>) fluctuating on a scale
of  100 pc, that the
tension in such a strong <B>
would permit the free swirling and
mixing of magnetic flux which is needed to explain an eddy diffusion
corresponding to
100 pc, that the
tension in such a strong <B>
would permit the free swirling and
mixing of magnetic flux which is needed to explain an eddy diffusion
corresponding to
 t
t
 1025
cm2 s-1.
Such swirling and mixing are what is required to make large scale
fields dissipate in 108 yr. Also, such turbulent mixing down
to these small scales (a scenario favored by
Kulsrud arid Anderson
1992)
would imply the generation of much stronger small scale fields - for
which there is no observational evidence. Observational
indications of fluctuations with
1025
cm2 s-1.
Such swirling and mixing are what is required to make large scale
fields dissipate in 108 yr. Also, such turbulent mixing down
to these small scales (a scenario favored by
Kulsrud arid Anderson
1992)
would imply the generation of much stronger small scale fields - for
which there is no observational evidence. Observational
indications of fluctuations with

 1011 cm
have been found by
Lee and Jokipii (1976)
but they are probably small amplitude, linear Alfvén waves which are
unable to reduce galactic Joule dissipation rates down to the
1011 cm
have been found by
Lee and Jokipii (1976)
but they are probably small amplitude, linear Alfvén waves which are
unable to reduce galactic Joule dissipation rates down to the
 108 yr
required to make the conventional galactic
108 yr
required to make the conventional galactic
 -
-
 dynamo work (cf
Parker 1992).
Similar doubts about the effectiveness of the diffusivity term in the
standard dynamo theory have been raised by
Knobloch and Rosner
(1981),
and Rosner and DeLuca
(1989),
who emphasized, among other things, the likelihood of the galactic
dynamo operating significantly out of the thin galactic
disk. Numerical simulations of thick disk dynamos have meanwhile
been undertaken by Moss and Tuominen (cf
section 2.3.3 above), and others.
dynamo work (cf
Parker 1992).
Similar doubts about the effectiveness of the diffusivity term in the
standard dynamo theory have been raised by
Knobloch and Rosner
(1981),
and Rosner and DeLuca
(1989),
who emphasized, among other things, the likelihood of the galactic
dynamo operating significantly out of the thin galactic
disk. Numerical simulations of thick disk dynamos have meanwhile
been undertaken by Moss and Tuominen (cf
section 2.3.3 above), and others.
Does the  -
-
 dynamo, despite some
observational support, therefore not work?
Or is there something missing? What the conventional literature on the
mean-field
dynamo, despite some
observational support, therefore not work?
Or is there something missing? What the conventional literature on the
mean-field  -
-
 dynamo does not examine
is the detailed
spatial and temporal nature of the (relativistic) cosmic ray gas,
provided by supernovae and pulsars, and the non-relativistic hot
gas (105 -107 K) from active sites of star
formation, i.e. large H II
complexes and associations of O and B stars. It also ignores the
recently verified existence of organized
outflow from such sites - especially in the nuclear region. Such
complexes can inject an additional energy density
dynamo does not examine
is the detailed
spatial and temporal nature of the (relativistic) cosmic ray gas,
provided by supernovae and pulsars, and the non-relativistic hot
gas (105 -107 K) from active sites of star
formation, i.e. large H II
complexes and associations of O and B stars. It also ignores the
recently verified existence of organized
outflow from such sites - especially in the nuclear region. Such
complexes can inject an additional energy density
 CR
+
CR
+  *
(the latter due to ionizing radiation and non-relativistic hot gas from
young star complexes) which is
*
(the latter due to ionizing radiation and non-relativistic hot gas from
young star complexes) which is
 10-11 erg
cm-3 over
10-11 erg
cm-3 over
 100 pc or more.
This can be an order of magnitude larger than the other energy
densities in (2.10). Furthermore, symmetric outflow would destroy the
symmetry of field sense above and
below the plane which was illustrated in figure 5.
Also, over a few × 108 yr, several of these transient
(
100 pc or more.
This can be an order of magnitude larger than the other energy
densities in (2.10). Furthermore, symmetric outflow would destroy the
symmetry of field sense above and
below the plane which was illustrated in figure 5.
Also, over a few × 108 yr, several of these transient
( *
*
 197
yr) `events' will occur at random over a galaxy's disk, and their
effect will be to disrupt any long term monotonic mean-field dynamo
build-up of a large scale field.
197
yr) `events' will occur at random over a galaxy's disk, and their
effect will be to disrupt any long term monotonic mean-field dynamo
build-up of a large scale field.
A related point is that the combination of the supernovae and O and B stars can produce `galactic fountains' (Shapiro and Field 1976, Bregman 1980, Cox 1981, Edgar and Chevalier 1986 and Kahn 1981), and more generally, galactic winds (cf Holzer and Axford 1970, Mathews and Baker 1971, Bardeen and Berger 1978, Habe and Ikeuchi 1980, Völk et al 1990, Breitschwerdt et a1 1991). These phenomena will naturally tend to drive significant outflow from galactic disks. At this point it is relevant to mention the more extreme case of a starburst nucleus, which creates an even stronger outflow, such as recently revealed in M82 (cf section 3.1 below).
The effectiveness of the standard
 -
-
 dynamo has been
questioned from another standpoint by
Kulsrud (1986),
who points out that the galactic disk field is tied largely
to the densest clouds, which are ipso facto the most neutral
clouds, so that the cloud-field coupling is not strong enough to prevent
the field from simply passing through the
clouds with the largest kinetic energy density. Thus the competing
effects just mentioned would, according to Kulsrud, prevent a tight
wind-up, or significant dynamo field generation (cf also
Kulsrud 1990).
dynamo has been
questioned from another standpoint by
Kulsrud (1986),
who points out that the galactic disk field is tied largely
to the densest clouds, which are ipso facto the most neutral
clouds, so that the cloud-field coupling is not strong enough to prevent
the field from simply passing through the
clouds with the largest kinetic energy density. Thus the competing
effects just mentioned would, according to Kulsrud, prevent a tight
wind-up, or significant dynamo field generation (cf also
Kulsrud 1990).
These phenomena have two broad implications for extragalactic magnetic
fields: (a) they appear to force a re-examination of how large scale
fields are generated and amplified in galaxies - which is our concern
in this section. (b) As we shall discuss in
section 6, they may have profound
implications for the origin and
strength of extragalactic magnetic fields. If the slow-acting (over
several × 108 yr) mean field
 -
-
 dynamo is
not effective, or is regularly disrupted by enhanced star formation
activity, then µG-level fields may have existed at the
protogalaxy stage. As we discuss later, there is
increasing evidence to suggest that this may have been the
case. Meanwhile we review some further developments of the mean-field
galactic dynamo theory.
dynamo is
not effective, or is regularly disrupted by enhanced star formation
activity, then µG-level fields may have existed at the
protogalaxy stage. As we discuss later, there is
increasing evidence to suggest that this may have been the
case. Meanwhile we review some further developments of the mean-field
galactic dynamo theory.
2.3.6. A modified galactic dynamo incorporating the
effects of ouflow. The energetic
nature of the stellar events mentioned above will produce some vertical
waviness in the galaxy disk field, thus permitting the dense gas to
slide downward along the field lines, while the buoyant and energetic
cosmic ray gas tends to inflate the outward-directed
wave bulges (cf
Mouschovias 1974,
Parker 1966,
1979 pp 325-33,
1992, and
Shibata et al 1989,
1990).
This `bulging and looping' of the disk mean field lines is associated
with an interstellar gas clumping scale of
 500 pc
over
500 pc
over  2 ×
107 yr - the characteristic
lifetime of the star-forming complexes mentioned above. The ongoing
generation of cosmic rays in the gaseous disk will produce ballooning
loops of field, which are inflated
outward at > 30 km s-1 to distances of
2 ×
107 yr - the characteristic
lifetime of the star-forming complexes mentioned above. The ongoing
generation of cosmic rays in the gaseous disk will produce ballooning
loops of field, which are inflated
outward at > 30 km s-1 to distances of
 1 kpc, thus
forming a halo above the disk (cf
Parker 1966,
1990,
1992,
Kahn 1991).
1 kpc, thus
forming a halo above the disk (cf
Parker 1966,
1990,
1992,
Kahn 1991).
In Parker's (1992)
proposed modified
 -
-
 dynamo, the resulting
close-packed, and outwardly inflating loops provide a natural
opportunity for rapid magnetic reconnection
between opposing, vertically oriented magnetic field lines (see
figure 6). This, plus the rapid outward
diffusion of the close-packed magnetic lobes provide the diffusivity
(
dynamo, the resulting
close-packed, and outwardly inflating loops provide a natural
opportunity for rapid magnetic reconnection
between opposing, vertically oriented magnetic field lines (see
figure 6). This, plus the rapid outward
diffusion of the close-packed magnetic lobes provide the diffusivity
( t)
which is otherwise difficult to physically justify on the `standard`
dynamo model (section 2.3.5). Another `natural'
feature of Parker's
model is that the outwardly inflated magnetic loops can sever
themselves, by reconnection, from the disk field. They then behave
as `freely rotating' loops due to the Coriolis force. Further
reconnection fuses the large
number of loops into a large scale poloidal field. This scenario appears
capable of explaining, a1 least qualitatively, the observed halo field
geometry in
Sukumar and Allen's
(1991)
observations of NGC 891, as do also the numerical models of
Brandenburg et al
(1992) and
Elstner et al (1992).
A key, and attractive aspect of Parker's
modified
t)
which is otherwise difficult to physically justify on the `standard`
dynamo model (section 2.3.5). Another `natural'
feature of Parker's
model is that the outwardly inflated magnetic loops can sever
themselves, by reconnection, from the disk field. They then behave
as `freely rotating' loops due to the Coriolis force. Further
reconnection fuses the large
number of loops into a large scale poloidal field. This scenario appears
capable of explaining, a1 least qualitatively, the observed halo field
geometry in
Sukumar and Allen's
(1991)
observations of NGC 891, as do also the numerical models of
Brandenburg et al
(1992) and
Elstner et al (1992).
A key, and attractive aspect of Parker's
modified  -
-
 dynamo is that it is a
fast dynamo, whose `speed' increases with disk
activity (i.e. outflow force). Whereas the conventional mean-field
dynamo amplifies the azimuthal disk field slowly over
dynamo is that it is a
fast dynamo, whose `speed' increases with disk
activity (i.e. outflow force). Whereas the conventional mean-field
dynamo amplifies the azimuthal disk field slowly over
 109 yr or
more, and is
susceptible to inevitable disruption by outflow due to disk star
formation activity, Parker's fast acting dynamo thrives
on the outflow; indeed it is the source of the turbulent
diffusivity. The more vigorous the outflow, the faster, and more
effective is the dynamo action.
109 yr or
more, and is
susceptible to inevitable disruption by outflow due to disk star
formation activity, Parker's fast acting dynamo thrives
on the outflow; indeed it is the source of the turbulent
diffusivity. The more vigorous the outflow, the faster, and more
effective is the dynamo action.
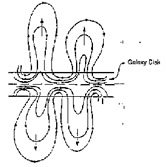 |
Figure 6. Illustration of the formation of vertical magnetic loops, inflated by cosmic rays and hot gas, which can detach by reconnection from the disk field (Parker 1994). |