


5.3. Probes of cosmological magnetic field evolution using quasar Faraday rotation statistics
The fact that no Faraday rotation `signal' has yet been detected from a
widespread, all-pervading intergalactic plasma
(section 5.1), whereas discrete
`magnetized cloud systems' have been detected over a similar redshift
range (section 5.2), indicates that
population models can be constructed for the latter, which can be tested
against RM observations of quasars out to significant lookback times in
the universe.
Welter et a1 (1984)
have produced comprehensive models of this type which they have tested
against the best RM data available about a decade ago, and concluded
that the RM intervenor population shows clear evolutionary effects out
to z  2.2. However
the data were not
sufficient to confidently isolate a particular preferred intervenor model.
2.2. However
the data were not
sufficient to confidently isolate a particular preferred intervenor model.
The mathematical modeling of discrete sources of RM as a function of z is different from that of the more straightforward case of calculating the `intersection depth' of a sample of intervenors for different cosmological geometries. The latter can be represented as an `optical depth'
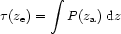 |
(5.6) |
where P(za) is the probability of intersection by a
cloud which has some number density,
n(za) = n0(1 +
z)3, and a (dimensionless) cross section,
A(za) = cn(za) /
H0{ 0(1 + za)
0(1 + za) }.
Here,
}.
Here,  is the
physical cross section of the RM intervenor, whose
cosmic evolution we parameterize by
is the
physical cross section of the RM intervenor, whose
cosmic evolution we parameterize by
 , following the
notation of
Welter et al (1984).
The subscript 0 refers to the present epoch. Consequently,
, following the
notation of
Welter et al (1984).
The subscript 0 refers to the present epoch. Consequently,
 (ze)
can be written in terms of A0, and making
use of equations (5.2) and (5.6), as
(ze)
can be written in terms of A0, and making
use of equations (5.2) and (5.6), as
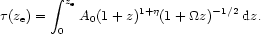 |
(5.7) |
This is a purely geometrical term, applicable to the calculation of
 for any intervenor, whose electromagnetic properties have yet to be
specified. If we assume
for any intervenor, whose electromagnetic properties have yet to be
specified. If we assume
 = 0, it integrates
easily to become
= 0, it integrates
easily to become
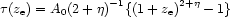 |
(5.8) |
Only small numbers of galaxy-scale intersections occur per quasar out to
z  3.3 (see e.g.
Khari-Joshi and Perry
1982).
More importantly, because of the
(1 + za)-2
`watering down' effect on a Faraday RM ( RMi for the
ith cloud) generated at za, the
probability density function
(Re(RMi, ze)) for
the total RM due to the (few) intervenors
between us and ze, must include the sum over all
combinations of RM, which, in turn, must be summed over all combinations of
za. For example, two clouds of comparable
RMi at two large zas (more probable) will
generate a smaller observed RM (depending on
3.3 (see e.g.
Khari-Joshi and Perry
1982).
More importantly, because of the
(1 + za)-2
`watering down' effect on a Faraday RM ( RMi for the
ith cloud) generated at za, the
probability density function
(Re(RMi, ze)) for
the total RM due to the (few) intervenors
between us and ze, must include the sum over all
combinations of RM, which, in turn, must be summed over all combinations of
za. For example, two clouds of comparable
RMi at two large zas (more probable) will
generate a smaller observed RM (depending on
 ) than the same
two clouds at low za (less probable), assuming no
cosmic evolution of RMi.
) than the same
two clouds at low za (less probable), assuming no
cosmic evolution of RMi.
Since the possibility of evolution needs to be introduced in a statistical model describing the Faraday RM strength of the clouds, we express the latter as an RMS (following Welter et al 1984);
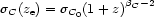 |
(5.9) |
and
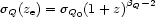 |
(5.10) |
where C, and Q apply to RM generated in any intervening clouds, and that associated with the quasar, respectively. The subscript 0 refers to the present epoch, as before.
Welter et al (1984),
using these concepts, developed appropriate general mathematical
formalisms which can be used to deduce, or limit the parameters
 C, A,
C, A,
 C,
C,
 Q
and
Q
and  . They show
that the measured
. They show
that the measured  2(ze), which
they determined from a sample
of 116 quasar RMS indicates significant evolution (namely
2(ze), which
they determined from a sample
of 116 quasar RMS indicates significant evolution (namely
 C
and/or
C
and/or
 Q
> 0), and that,
if future RM samples enable a precise specification of the fraction of
non-intersections (f0), it should be possible in
future to specify
all of the above unknowns. This information, together with future
high resolution absorption spectra for the same quasars, will
provide fairly direct data on the evolution of Faraday rotating
intervenors. out to the most distant quasars. This is an exciting
prospect, in that it can potentially generate magnetic field estimates
over > 90% of the Hubble time.
Q
> 0), and that,
if future RM samples enable a precise specification of the fraction of
non-intersections (f0), it should be possible in
future to specify
all of the above unknowns. This information, together with future
high resolution absorption spectra for the same quasars, will
provide fairly direct data on the evolution of Faraday rotating
intervenors. out to the most distant quasars. This is an exciting
prospect, in that it can potentially generate magnetic field estimates
over > 90% of the Hubble time.
The existence of a significant fraction (f0) of
quasars which do not
intersect an intervenor was indicated in the analysis of
Kronberg and
Simard-Normandin (1976).
It is additionally interesting in that, independent of the `discrete
intervenor' properties discussed here, improved precision in the
measurement of extragalactic RMs may in future either lower the limit
of null detection of a widespread IG magnetic field, or
possibly detect such a field, if |Bigm|0
 10-8.5
G (section 5.1).
10-8.5
G (section 5.1).