5.5. Seed field before the galaxy formation epoch

5.5.1. Magnetic field amplification between recombination and galaxy formation.     The formation scenarios for the first stars and galaxies between the recombination epoch (at z 1000), and the epoch of the currently visible quasars (z 0.2 to 5) are not yet well understood, and as noted, there are few observations into those epochs. The role and influence of magnetic fields is likewise unclear, however this pessimistic situation has not deterred efforts to propose mechanisms for the very early generation of magnetic fields.

Zweibel (1988) has considered a scenario in which post-recombination density fluctuations, combined with tidal torques arising between mass condensations causes regeneration of a seed field. The tidal torques lead naturally to rotation, which can cause field regeneration by processes discussed in section 2; namely the toroidal field component is wound up in rotation which, in tum via the Coriolis force acting on small scale fluctuations provides the helicity, and hence the basic elements of an - dynamo field regenerator. Zweibel's scenario incorporates cosmic expansion into the above scenario, and leads to estimates of up to ~ 10⁹G on scales of a few Mpc. This is close to current observationally established upper limits for a widespread IGM (cf section 5.1), but below what appears to be found in galaxy clusters (cf section 3.1). We might speculate that further magnetic field regeneration by, for example, matter infall along the lines of the model suggested by Pudritz and Silk (1989) might also provide interstellar-level fields already at this cosmological epoch, given a sufficient number of e-folding times.

If, as suggested by Kibble (1976), strings of supragalactic dimensions formed during the early universe then, as Ostriker et a1 (1988) argue, a fossil field is an essential ingredient. When magnetic fields, along with intergalactic plasma are swept up by a moving superconducting string, reconnection of the field lines occurs behind the string, thereby trapping plasma there. A relativistic MHD wind emanates from oscillating super-conducting loops, which carries a wound-up magnetic field (Thompson 1990). Such loops drive blast waves which, in Ostriker and Thompson's (1987) model, continuously heat the IGM for the recombination epoch onward. The magnetic field associated with the string-driven waves has a present-epoch value of a fraction of a µG. This proposed scenario can accommodate the experimentally established very low intergalactic density of neutral atomic hydrogen (Gunn and Peterson 1963, and also the current experimentally established upper limit of ~ 10^-9 G for a widespread IG field (cf section 5.3).

5.5.2. Models of magnetic field generation during the plasma epoch, before recombination.     An interesting scheme for generating fields before the recombination epoch (at which point z 10³, and the universe was ca 10¹³ s old), was proposed by Harrison (1970, 1973). At this time, the radiation field and particles were strongly coupled, but there is a differential coupling between the intense radiation field and the electrons and ions respectively, due to the more effective Thomson scattering for the electrons. A key proviso for Harrisons's mechanism is that the primordial perturbations at this epoch have a non-zero vorticity. The result is that the (co-moving) eddies in the photon-electron component of the primordial 'soup' have a slower decrease in angular velocity, as the scale factor, R, increases ( R^-1). By contrast, the ion component due to its larger rest mass, hence lower coupling, generates eddies for which R^-2. The difference between the two exponents causes an EMF, hence a current (analogous to the Biermann battery effect) and hence a back EMF which couples the electron and ion components of the eddies.

However, as Rees (1987b), and others point out, a significant vorticity at this epoch is difficult to reconcile with the expected predominance of irrotational density perturbations which, arising from initial curvature fluctuations, should become dominant in the post-recombination epoch. It is these fluctuations which are thought to be associated with the formation of protogalaxies.

Another field-generating scenario during this same, plasma epoch (1s < < 10¹³ s, or 10¹⁰ > z > 10³), which does not require vorticity, has been recently put forward by Tajima et al (1992). Based on the fluctuation-dissipation theorem (Kubo 1957), Tajima et a1 (1992) derive an expression for the magnetic field fluctuation at spectrum (in wavenumber and frequency space) in a plasma which is in thermal equilibrium - the 'least special' ab initio assumption. They find that <B²> / 8 is nearly Planckian at high frequencies, but that a narrow peak in <B²> / 8 occurs near = 0. This arises from two fundamental physical effects; first, the lifetime of the magnetic fluctuations, _B is ², being the scale size, so that larger 'bubbles' are favored at any given time. Second, a reinforcement of the magnetic structures stems from the purely geometrical fact that the largest bubbles also have the greatest cross section for reconnection-inducing bubble mergers. Tajima et al (1992) refer to these combined processes as magnetic polymerization; its effect is to generate a magnetic field just prior to the recombination epoch at 10¹³ s. The field strength although difficult to quantify, could be of order 10^-12 G, or possibly higher. The above assumptions and conditions become inapplicable after recombination, so that just what fields the first protogalaxies begin with is determined by other physical conditions, not specified in the above model. Tajima et al's seed field mechanism appears consistent with all other evidence, scant as that is, but importantly it specifies that both the sum of the magnetic + charged particle pressure, and the photon pressure, are virtually constant in space. Constancy of the latter thus does not violate the recent COBE results (cf Gush et al 1990). Unfortunately, there appears little prospect of verifying an observational imprint of these fluctuations of B, and/or their associated density fluctuations.

The resultant magnetic field, if projected to galactic scales at the first galaxy formation epoch, is of order 10^-18 G. Although weak, and dynamically insignificant, it could nonetheless provide the seed fields which, by some dynamo mechanism, might subsequently amplify up to the observed µG-level galactic fields.

5.5.3. Cosmological seed fields originating in the inflation epoch.     Turner and Widrow (1988) argue that if, as seems the case, intergalactic fields exist on the scale of a few Mpc, then inflation is a good candidate mechanism for their origin. Among their reasons are that inflation provides the means, through its kinematics, of producing very large scale phenomena via microphysical processes which operate on a sub-horizon scale; that the relatively low conductivity which precedes the highly conducting plasma epoch, i.e. during the inflation epoch, permits an early increase of magnetic flux. Using this general idea, Quashnock et al (l989) proposed a seed field generating mechanism which is based on the assumption of a first-order QCD phase transition, which occurs during the first 10 µs at T_c, where kT_c = 150 MeV (cf Fukugita 1988). Here the hadronic bubbles form out of a quark-gluon plasma on scales of 10^1±1 cm, where the nucleation sites are separated by ca 10 × that scale. This quark-gluon hadron transition possesses a characteristic temperature (T_c) due to a postulated mechanism whereby supersonic shock heating from the hadronic bubbles (which form a deflagration front) releases latent heat into the quark-gluon plasma. This heating compensates for the cooling due to cosmic expansion for the few microsecond duration of the phase transition. At this point in the model (at a Hubble time of 10µs) the quarks and gluons have been transformed into mesons and baryons (Kajantie and Kurki-Suonio 1986). Quasnock et al (1989) propose that currents are set up due to the co-existence of slightly positively charged quarks and negatively charged leptons. These have different equations of state. This results in an electric field being associated with the subsonically moving hadronic shock fronts. In Quasnock et al's model, the collision of these shock fronts and the consequent vorticity will, via a Biermann battery-like mechanism, cause the generation of ca 5 G magnetic fields on a scale of the distance between bubbles, which is 10^2±1 cm (see above). By invoking some further assumptions, including the local scale-related field diffusion time, they arrive at a field strength of ~ 2 × 10^-17 G on a scale of ~ 5 × 10¹⁰ cm at the recombination epoch. This scale is of order 1 AU at the present epoch - very small compared with galaxy scales, which makes it unclear whether such fields could effectively serve as seed fields in protogalaxy systems.

Vachaspati (1991) has suggested that gradients in the vacuum expectation value of the Higgs field give rise to magnetic fields, whose scale is related to the horizon scale after the QCD phase transition. This results in very weak fields, which could serve as seed fields. A similar scenario, though lacking firm predictions, has been proposed by Dolgov and Silk (1993). Dolgov and Silk propose that, if the gauge symmetry of electromagnetism is broken, then subsequently restored, the next electric charge density must vanish, and be compensated by heavy charged particles in the Higgs vacuum. Their decay products would cause an electric current, and a local charge asymmetry. They argue that these currents would create chaotic magnetic fields on 'astronomical' scales which could provide the seed field.

All of the above primordial field generating mechanisms predict very weak initial fields which, if they were the origin of current fields in galaxies and clusters, would need many e-folding times of dynamo amplification.

The generation of seed magnetic fields in the inflation period of the universe has also been considered by Ratra (1992a, b), who likewise proposes a sequence of scenarios beginning at the transition between the inflation and radiation eras. Ratra (1992a, b) explores the consequences of a coupling between , the scalar field which is responsible for inflation, and an Abelian gauge field (A_µ), where is the exponent in the inflation model. The proposed coupling is described by

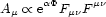(5.12)

where F_µ is the field-strength tensor of A_µ and is a parameter. Ratra's model extends over three epochs - that of scalar field dominance, the radiation dominant era (see above), and the baryon era. Allowing for various uncertainties in the physics, especially at transition points, Ratra arrives at a range of present-epoch fields, which range from 10^-65 to ~ 10^-10 G on a scale of a few Mpc. The higher fields, which arise from models close to the de Sitter inflation model with relatively large , would easily suffice to provide seed fields for subsequent regeneration during galaxy formation (e.g. through infall, or outflow), or some subsequent dynamo amplification due to outflow, rotation, etc.

5.5.4. Possible links between magnetic field generation, the masses of neutrinos, and nucleosynthesis.     Enqvist et a1 (1992) present an argument, based on current-epoch galactic magnetic fields, that the magnetic moment of Dirac neutrinos has an upper limit of 2.4 × 10^-16 Bohr magnetons. This is about five orders of magnitude below current laboratory or astrophysical measurements (cf Vergados 1991), but it is scaled by a somewhat uncertain value of B_seed and hence may not be quite so stringent. Their argument limits, in consequence, the sum of the masses of the all neutrinos (including unstable ones), hence the masses of muon and tau neutrinos (_µ and ). Subject to the uncertain B_seed value, it would lead to a limit on the combined masses of the latter two neutrino flavors - if the standard model is assumed. This follows, Enqvist et a1 argue, if the successful nucleosynthesis model of helium abundance is to be preserved, and if very large magnetic field strengths (B 10²³ - 10²⁴ G) existed at the electroweak transition phase, which are estimated by Vachaspati (1991) (cf previous section). Such large fields are implied by cosmic expansion, even if seed fields were as weak as 10^-30 G on a scale of 100 kpc (present epoch) (Enqvist et a1 1992). In a more recent, similar analysis Enqvist et a1 (1993) introduce a lower limit of 3 × 10^-13 G to the seed field strength at galaxy formation, which is tied to an interpretation of the recent GALLEX neutrino experiment results (Anselmann et al 1992), based on the MSW theory of matter-induced neutrino oscillations. New, complementary ground-based estimates of the combined masses of all neutrino flavors, independent of oscillations between (_e, _µ, and ), might be possible with the Sudbury Neutrino Observatory (SNO) currently under construction (Ewen 1992).

The above analysis rests, of course, on the assumption of dynamo amplification in galaxies of a seed field whose origin was around the time of the QCD phase transition, when the cosmic temperature was 200 MeV. The above arguments would be rendered invalid if, possibly consistent with the observations we discussed in section 3, the seed fields were produced much later, in the first stars and galaxies. In other words, this particular `link` between galactic magnetic fields and particle physics in the early universe would be broken, and the corresponding limits on neutrino magnetic moments and masses would not apply. This discussion illustrates in any case that magnetic field generation near the epoch of the QCD phase transition is of fundamental importance for cosmological theory and particle physics, and that the investigation of cosmic magnetic fields has potentially close connections to fundamental physics.