3. EXTRASOLAR PLANETS

The solar system was not the only place to provide for planetary drama. During the past eight years we have witnessed the number of known extrasolar planets orbiting Sun-like stars going from zero to about one hundred at the time of this writing! The human fascination with the possibility of discovering extraterrestrial life has helped turn planet detection into one of the major frontiers of today's astronomy.

The Hubble Space Telescope's contributions to this exciting field have been related mostly to the discovery of circumstellar disks from which planets form, and these will be described in Section IV. In two cases, however, HST has produced three truly unique sets of observations, one in a globular star cluster, and two following the light curve and spectrum of a transiting planet.

3.1. Where have all the planets gone?

The discovery of a planet orbiting the star 51 Peg (Mayor and Queloz 1995) in a remarkably tight orbit of 4.231 days challenged prevailing theoretical views and marked the start of a "Golden Age" in planet discoveries by radial velocity surveys (see, for example, Marcy et al. 2000). The existence of gas giant planets in very close orbits (at 0.04-0.05 AU) enables even photometric searches for these planets ("hot Jupiters"). At such small separations, the probability of the planet transiting ("eclipsing") the parent star, given random orbital inclinations, is about 10%. More precisely, from Kepler's laws, the duration of a transit in hours (reduced by / 4 for average chord length) is given by

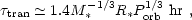(4)

where M_*, R_* are the stellar mass and radius in solar units and P_orb is the orbital period in days. The probability of a transit per system is given by

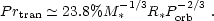(5)

Transits are very important because of the following reasons: (a) With transits one can immediately obtain the size of the planet [the transit depth is equal to (R_p / R_*)²]. (b) In the case of transits, measurements of radial velocities immediately provide the planet's mass (and not just m_psin i, where i is the otherwise unknown orbital inclination). (c) A knowledge of the mass and radius can be used to test theoretical mass-radius relations for close-orbiting planets.

In 1998, a team of astronomers led by Ron Gilliland of the Space Telescope Science Institute embarked on the ambitious program of searching for transits in some 40,000 stars in the core of the globular cluster 47 Tucanae (Fig. 7). This cluster is a particularly interesting target for such a search for several reasons. (i) For a typical star in the cluster, M_* = 0.81, R_* = 0.92, and a typical "hot Jupiter" orbital period (e.g., P_orb = 3.8 days), the probability of transit is 9.6% and the duration is 2.2 hours. For a planet of radius R_p = 1.3 R_J (where R_J is Jupiter's radius, as observed for the transiting system HD 209458; Charbonneau et al. 2000, Henry et al. 2000), the expected transit depth is about 2%, easily detectable by HST. (ii) Given that the frequency of "hot Jupiters" with orbital periods shorter than 5 days (ten are known at the time of writing) in the solar neighborhood is about 0.8%-1%, with a 10% chance of transit one expects roughly one in every 1000 surveyed stars in 47 Tuc to show a transit (and therefore a few tens of detections when monitoring ~ 40, 000 stars). (iii) The globular cluster 47 Tuc is about 11 billion years old and it has a total metallicity (abundance of elements heavier than helium) of about one-third that of the Sun (Salaris and Weiss 1998). The frequency of planets in such an environment can therefore have important implications for models of planet formation.

Figure 7. Globular Cluster 47 Tucanae (NGC 104), HST/WFPC2, July 1999. Credit: NASA and R. Gilliland (STScI). http://hubblesite.org/newscenter/archive/2000/33/

The Hubble Space Telescope observed 34,091 stars in 47 Tuc, obtaining time series photometry over a period of 8.3 days (continuously, except for Earth occultations and passages through the South Atlantic Anomaly). A more detailed calculation of the expected number of transits, taking into account the actual distribution of V magnitudes of the stars in the sample (Gilliland et al. 2000) and time series noise, showed that 17 transits should have been seen, assuming the same frequency of hot Jupiters as in the solar neighborhood. None was detected! Undoubtedly, this was not a problem with the detection method. As many as 75 variable stars have actually been detected. Furthermore, an eclipsing system with a period of 1.34 days and an eclipse depth of ~ 3% was actually discovered. However, the presence of a secondary eclipse in the system showed that this was a grazing eclipse by a low-mass (K dwarf) star and not a planet.

The direct implication is therefore that with a very high degree of confidence the frequency of hot Jupiters in 47 Tuc is at most 1/10 that in the solar neighborhood.

The main question is then: why are there much fewer orbiting planets in 47 Tuc? There are, in principle, two possible explanations for the paucity of planets in orbits around globular cluster stars: (i) Planets do not form at all (or form much more rarely) in globular clusters. (ii) Planets are torn from their parent stars.

Planet formation may be suppressed in old stellar clusters because of two main reasons: low metallicity, or photoevaporation of protoplanetary disks.

Conventional wisdom of giant planet formation suggests that this is a two-step process. In the first, the collisional accumulation of rocky and big planetesimals leads to a runaway growth of a solid core (e.g., Lissauer 1987) of about ten Earth masses (10 M). In the second, the core acquires a gaseous atmosphere, which eventually collapses, leading to the rapid accretion of hydrogen and helium from the protoplanetary disk. One might suspect, therefore, that in low-metallicity environments, the nucleation of dust grains would be greatly suppressed, and concomitantly planets would form more rarely. Furthermore, it has generally been noted that stars which bear planets are, on average, enriched in metals in comparison to the Sun (e.g., Gonzalez 1997, Butler et al. 2000, Laughlin 2000, Reid 2002), and this trend is even more pronounced for the short-period planets. Thus, the paucity of hot Jupiters in 47 Tuc may simply reflect the cluster's low metallicity.

There is another reason why giant planet formation may be suppressed in dense stellar clusters. The disk around any star in a cluster is exposed to ultraviolet radiation from massive cluster stars. This radiation heats the disk surface, raises the sound speed, c_s, and causes gas beyond a radius of

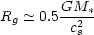(6)

to become unbound and flow away as a thermal wind. The mass-loss rate in such a photoevaporation flow scales as (e.g., Bertoldi and McKee 1990, Johnstone et al. 1998)

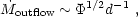(7)

where is the flux of ionizing photons and d is the disk's distance from the emitting source. In a star forming region like Orion, the ionizing flux is of order ~ 10⁴⁹ s^-1, of the same order as the flux expected in a cluster with n_cluster ~ 10³ members. The mass loss rate from one of the disks in Orion, HST 182-413, has been estimated from HST observations to be _outflow ~ 4 × 10^-7 M yr^-1. Since the mass of that disk is estimated to be Johnstone et al. 1998) M_disk ~ 0.04 M, the disk lifetime is expected to be _disk ~ M_disk / _outflow ~ 10⁵ yr. For somewhat smaller disk sizes (e.g., like that in the solar system ~ 30 AU) the disk lifetime can be somewhat extended (the EUV-induced flow scales as r_disk^3/2). Nevertheless, the disk lifetime may be significantly shorter than the planet formation timescale, estimated to be of order 10⁶-10⁷ yrs (e.g., Shu et al. 1993, Pollack et al. 1996). Armitage (2000) calculated the expected disk lifetime as a function of the cluster richness. He found that giant planet formation is strongly suppressed in custers with ~ 10⁵ stars out to around 1 pc or more.

There are two ways in which, in principle at least, the conclusion of a low probability for planet formation in clusters, due to disk destruction, may be avoided: (i) If giant planet formation occurs not via a core accretion mechanism, but rather through direct and rapid (within ~ 10³ yr) fragmentation (due to a gravational instability) into self-gravitating clumps of gas (e.g., Boss 2000, Mayer et al. 2002). (ii) If the formation of high-mass stars (which produce the photoevaporating radiation) is significantly delayed (by ~ 10⁶ yr) compared to the formation of low mass stars. At present both of these processes are sufficiently uncertain that no definitive conclusion about their viability can be drawn.

The second possible explanation for the absence of "hot Jupiters" in 47 Tuc is that even if giant planets do form, they are torn away from their parent stars because of encounters in the crowded cluster environment, and thus cannot exhibit transits. This possibility has been investigated in some detail by Davies and Sigurdsson (2001). The cross-section for two stars with a relative velocity at infinity V to pass within R_min from each other is given by

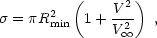(8)

where V is the relative velocity (V² (M₁ + M₂) / R_min) at closest approach. The second term expresses the effect of gravitational focusing. When V >> V, as is expected in globular clusters, R_min. The timescale for an encounter between a star-planet system and a star is of order (_enc = 1/n V)

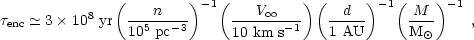(9)

where n is the number density of stars of mass M and d is the semimajor axis of the planetary orbit. Encounters therefore occur on a timescale that is much shorter than a Hubble time in a cluster like 47 Tuc, which has a density of about 1.5 × 10⁵ pc^-3 at its center and about an order of magnitude lower at its half-mass radius (e.g., Howell et al. 2000). Generally, binaries (with masses M₁ and M₂ for the primary and secondary, respectively) in which the binding energy is lower than the kinetic energy of the colliding star (of mass M₃) are disrupted. The condition for breakup is

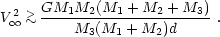(10)

Since M₂ << M₁, M₃, in the case of a star-planet system, breakup of the system is expected to occur with a high probability when the third star passes within a distance d. Davies and Sigurdsson (2001) performed a large number of simulations for various values of V / V_orb and considered both encounters (of star-planet systems) with single stars and with binaries. They found that wide (d 0.3 AU) planetary systems are likely to be broken up within the half-mass radius of 47 Tuc, but tighter systems (d 0.1 AU) or systems in less dense regions may survive. The results of Davies and Sigurdsson still do not provide a complete explanation for the absence of transits in 47 Tuc. Future observations, perhaps of less dense, somewhat higher metallicity clusters (like NGC 6352) will be required to explain which factor is responsible for the dearth of planetary transits in 47 Tuc. An attempt to detect transits associated with Galactic bulge and disk stars (that span 1.5 dex in metallicity, and are in an environment that is orders of magnitude less dense than the center of a globular cluster) would also be very valuable. An understanding of the environments that are either conducive to or prohibitive for the existence of planetary transits may constitute an important step in the study of planet formation.