


5.1. Search techniques for supermassive black holes
The actual searches for supermassive black holes rely primarily on stellar- and gas-dynamical evidence (see, e.g., Kormendy and Richstone 1995, for a review). In particular, the idea is to unambiguously show that the mass-to-light ratio, M/L, increases toward the galactic center to values that are difficult to accomodate with other types of stellar populations. Ideally, one would want to follow this up with the detection of relativistic speeds, but at present even HST cannot resolve orbits at a few gravitational (Schwarzschild) radii (RS = 2GMBH / c2; where MBH is the black hole mass, G is the gravitational constant and c is the speed of light).
Generally, the basic principle behind the early stellar-dyamical search techniques can be explained by the following, simplified picture. Taking the first velocity moment of the collisionless Boltzmann equation gives
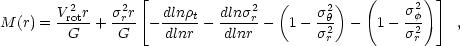 |
(15) |
where M(r) is the mass enclosed within radius r,
Vrot is the rotational velocity,
 r,
r,

 ,
,

 are the
components of the velocity dispersion, and
are the
components of the velocity dispersion, and
 t is
the density of the tracer stars being observed (usually assumed to be
proportional to the volume brightness). A direct measurement of
t is
the density of the tracer stars being observed (usually assumed to be
proportional to the volume brightness). A direct measurement of
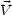 rot
and
rot
and 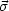 , therefore
can determine the central mass. To actually use eq. 15, however, the
ranges of unprojected quantities (e.g.,
, therefore
can determine the central mass. To actually use eq. 15, however, the
ranges of unprojected quantities (e.g.,
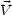 rot,
rot,
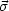 ) need to
be derived, and various techniques to achieve that have been developed
(see for example,
Kormendy 1988,
Dressler and
Richstone 1988,
van der Marel 1994,
Gerhard 1993).
) need to
be derived, and various techniques to achieve that have been developed
(see for example,
Kormendy 1988,
Dressler and
Richstone 1988,
van der Marel 1994,
Gerhard 1993).
The more recent search techniques fit axisymmetric, three-integral dynamical models of the galaxy (using the line-of-sight velocity distribution), to the observed light distribution. Basically, the orbits in the (R, z) plane in realistic galactic potentials are often found to have in addition to the two integrals of motion E (the energy) and Lz (the z-component of the angular momentum, where z is the symmetry axis), a third integral, I3, that can be associated with the approximately conserved total angular momentum, L.
The dynamical model assumes axisymmetry and an inclination for the galaxy and first determines the optimal density distributrion that is consistent withthe surface brightness distribution (making certain assumptions about M/LV). Then, a central point mass is added, and the potential calculated. Orbits that sample the phase space of the three integrals of motion are then calculated, and the data of the full line-of-sight velocity distribution are fitted to the models.
Since galactic gas is affected also by forces which are
non-gravitational (e.g., radiation pressure), stellar kinematics are
considered more secure than gas dynamics in black hole
searches. Nevertheless, in a few cases, the presence of the black hole
may be revealed by gas-dynamical searches. The prototype of this
technique is provided by the radio galaxy M87. Early stellar-dynamical
observations revealed that the velocity dispersion continues to rise
inward, to
r  1".5
(e.g.,
Sargent et al
1978,
Lauer et al. 1992).
However, due to the expected anisotropy in the velocity dispersion,
models without a black hole could also fit the observations (e.g.,
Binney and Mamon
1982,
Dressler and
Richstone 1990,
van der Marel
1994).
In particular, the last author found
1".5
(e.g.,
Sargent et al
1978,
Lauer et al. 1992).
However, due to the expected anisotropy in the velocity dispersion,
models without a black hole could also fit the observations (e.g.,
Binney and Mamon
1982,
Dressler and
Richstone 1990,
van der Marel
1994).
In particular, the last author found

 400 km s-1
at r
400 km s-1
at r  0".5, which could nevertheless be fitted with anisotropic models
that do not include a black hole.
0".5, which could nevertheless be fitted with anisotropic models
that do not include a black hole.
A more definitive answer, however, came in this case from the
gas. High-resolution HST observations of the nucleus revealed the
presence of a small gas disk (about 20 pc in radius), with a major
axis perpendicular to the optical jet (Fig. 20).
Spectra taken at two opposite points along the major axis (at a
luminosity-weighted mean radius of 16 pc) found emission lines
separated by 2V = 916 km s-1
(Ford et al.
(1994),
Harms et al.
(1994)).
For an inclination angle of the disk of
~ 42° (implied by the observed axis ratio), the observed velocity
amplitude (if interpreted as a circular Keplerian motion) corresponds to
a dark mass of
MBH  3
× 109
M
3
× 109
M at the center
of M87. These results have been further confirmed by
Macchetto et
al. (1997),
making the black hole in M87 the most massive
observed so far (with a relatively secure mass determination). I should
caution that an airtight case for circular Keplerian motion is still to
be made for M87. Incidentally, the best case for a black hole
based on gas dynamics is for the modest active galactic nucleus NGC 4258. In
that case, Very Long Baseline Array (VLBA) observations of high-velocity
masers show a rotation curve that can be fitted remarkably well with
Vrot(r)
at the center
of M87. These results have been further confirmed by
Macchetto et
al. (1997),
making the black hole in M87 the most massive
observed so far (with a relatively secure mass determination). I should
caution that an airtight case for circular Keplerian motion is still to
be made for M87. Incidentally, the best case for a black hole
based on gas dynamics is for the modest active galactic nucleus NGC 4258. In
that case, Very Long Baseline Array (VLBA) observations of high-velocity
masers show a rotation curve that can be fitted remarkably well with
Vrot(r)
 (832 ± 2)(r /
0.25 pc)-1/2 km s-1, implying a black hole mass
(mass interior to 0.18 pc) of
MBH
(832 ± 2)(r /
0.25 pc)-1/2 km s-1, implying a black hole mass
(mass interior to 0.18 pc) of
MBH  4.1 × 107
M
4.1 × 107
M .
.
 |
Figure 20. Jet and disk of stars and gas in the active galaxy M87, HST/WFPC2, 1994. Credit: NASA and H. Ford (JHU). http://hubblesite.org/newscenter/archive/1994/23/ |