5.2. The M_BH - relationship

Using three-integral models and HST spectroscopy, Gebhardt et al. (2000) were able to determine black hole masses in 16 galaxies. Adding to these two galaxies with maser mass determinations (NGC 4258 and NGC 1068), six galaxies with black hole masses determined by gas dynamics, and our own galaxy (Ghez et al. (1998), Genzel et al. (2000)) and M31 (Dressler and Richstone (1988)), they were able to discover a tight correlation between the black hole mass and the velocity dispersion in the galactic bulge. Specifically, they found that

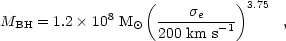(16)

where _e is the line of sight aperture dispersion within the half-light radius R_e. The obtained relation is much tighter (Fig. 21, right) than a previously determined relation (e.g., Magorrian et al. 1998) between black hole mass and the bulge luminosity (Fig. 21, left). Based on a smaller sample (12 galaxies), Ferrarese and Merritt (2000) found independently a M_BH relation, with a somewhat steeper slope of ~ 4.8.

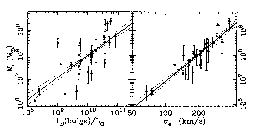Figure 21. Black hole mass versus bulge luminosity (left), and the luminosity-weighted dispersion (right). Adopted from Gebhardt et al. (2000).

Clearly, the observed tight M_BH - correlation strongly suggests that the formation and evolution of the bulge and of the black hole are causally connected. The precise nature of this connection, however, is still a matter of considerable uncertainty. A relatively simple theoretical model for the relation has been suggested by Adams, Graff and Richstone (2001).

In this model, a slowly rotating isothermal sphere (with a seed central black hole) collapses to form the bulge (the dark matter is assumed to move in tandem with the baryons). The density distribution is assumed to be of the form

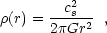(17)

where c_s is the speed of sound. Note that for dissipationless collapse the velocity dispersion is roughly given by ² 2c_s². The region is assumed to rotate rigidly (due to effective tidal torques) at an angular speed , and the specific angular momentum is j = r² sin² , where r is the initial radius and is the polar angle. For zero-energy orbits, the pericenter distance in the equatorial plane is therefore

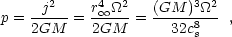(18)

where in the last equality we used the fact that for the assumed density distribution M(r) = 2c²_s r / G. For material to be captured by the black hole we need p 4R_S, where R_S is the gravitational (Schwarzschild) radius R_S = 2GM / c². Using eq. 18, the condition p = 4R_S therefore reads (assuming that the capture condition defines the black hole mass)

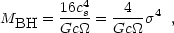(19)

in good agreement with the observed relation (eq. 16).

Other considerations result in similar expressions. For example, in a protogalaxy modeled as an isothermal sphere of cold dark matter, with (r) = ² / 2 Gr², with a fraction f_gas in the form of gas, a central, accreting black hole will generate an intense wind outflow. The black hole itself may be assumed to form by coherent collapse before most of the bulge gas turns into stars. If the black hole radiates at the Eddington luminosity, L_EDD = 4cGM_BH / (at which gravity is balanced by radiation pressure; where is the electron scattering opacity), and a fraction f_out is deposited into kinetic energy of the outflow, then a shell of swept-up material will be moving outward at a speed

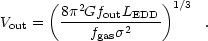(20)

The condition that the shell would escape, and therefore, that the black hole would unbind the bulge gas, requires V_out > . This implies that the black hole mass is limited by (Silk and Rees (1998))

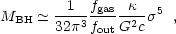(21)

similar to the relation found by Ferrarese and Merritt (2000).

Semi-analytical, hierarchical galaxy formation models (see Section VI), in which galaxies form by merging halos (and merging central black holes), with simple prescriptions for gas cooling, star formation, and feedback from supernovae, also tend to produce scalings of the form M_BH ~ ⁴ (for example, Haehnelt and Kauffmann 2000). Broadly speaking, this relation can be traced to the facts that: (i) In mergers, the black hole mass scales with the halo mass. (ii) ~ ^1/6 M_halo^1/3, and (iii) M_halo scales like ^-2 in typical cold-dark-matter cosmologies (really like ^-2/(3+n), where n ~ - 2 is the slope of the dark matter fluctuations spectrum). Combining (i)-(iii) gives M_BH ~ ⁴.

Somewhat more exotic scenarios, which involve the accretion of collisional dark matter (invoked to make galactic halos less dense; for example, Spergel and Steinhardt 2000), also produce black hole masses which scale roughly with ^4.5 (Ostriker 2000).