Probing the Universe with Weak Lensing

Annu. Rev. Astron. Astrophys. 1999. 37: 127-189
Copyright © 1999 by Annual Reviews. All rights reserved

4.1. Theoretical Expectations

The theoretical investigations of the effect of the large-scale mass distribution on the distribution of ellipticity/orientation of distant galaxies are somewhat simplified by the low density contrast of structures. Beyond 10 Mpc scales, delta rho / rho approx 1 and linear perturbation theory can be applied. On these scales, lenses are no longer considered individually but they are now viewed as a random population which has a cumulative lensing effect on the distant sources. Blandford (1990), Blandford et al (1991), Miralda-Escudé (1991) first investigated the statistical distribution of distortions induced by large-scale structures in an EdS universe. They computed the two-point polarization (or shear) correlation function and established how the rms value of the polarization depends on the power spectrum of density fluctuations. Kaiser (1992) extended these works and showed how the angular power spectrum of the distortion is related to the three-dimension mass density power spectrum, without assumptions on the nature of fluctuation. These works were generalized later to any arbitrary value of Omega by Villumsen (1996), Bar-Kana (1996). All these studies concluded that the expected rms amplitude of the distortion is of about one percent, with a typical correlation length of a degree. Therefore it should be measurable with present-day telescopes.

These promising predictions convinced many groups to start investigating more thoroughly how weak lensing maps obtained from wide field imaging surveys could constrain cosmological scenarios. To go into further detail, it is necessary to generalize the previous works to any cosmology and to describe in detail observables and physical quantities that could be valuable to the constraint of cosmological models. Indeed, the investigations of weak lensing by large-scale structures require theoretical and statistical tools that are not different from those currently used for catalogues of galaxies or cosmological microwave background (CMB)-maps. In this respect, the perturbation theory, which has already been demonstrated to work, describes the properties of large-scale structures very well (see Bouchet 1996 and references therein), and seems to be an ideal approach for such large scales. In addition, the use of similar statistical estimators for catalogues of galaxies seems perfectly suited. Bernardeau et al (1997) used the perturbation theory to explore the sensitivity of the second and third moments of the gravitational convergence kappa (rather than the distortion whose third moment should be zero), to cosmological scenarios, and to cosmological parameters, including lambda -universes. The small angle deviation approximation implies that the distortion of the ray bundle can be computed on the unperturbed geodesic (Born approximation). In the linear regime, if lens-coupling is neglected (see Section 4.4.3), the cumulative effect of structures along the line of sight generates a convergence in the direction theta ,

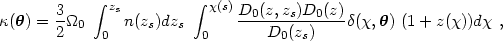$\begin{equation} \kappa(\thetag)={3 \over 2} \Omega_0 \ \int_0^{z_s} n(z_s) dz_s \ \int_0^{\chi(s)} {D_0(z,z_s) D_0(z) \over D_0(z_s)} \delta(\chi,\thetag) \ (1+z(\chi)) d\chi \ , \end{equation}$

(29)

where chi is the radial distance, D₀ is the angular diameter distance, n(z_s) is the redshift distribution of the sources, and

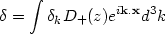$\begin{equation} \delta = \int \delta_k D_+(z) e^{i \boldk.\boldx} d^3 k \end{equation}$

(30)

is the mass density contrast, which depends on the evolution of the growing modes with redshift, D₊(z). It is related to the power spectrum as usual: < delta _k delta _k' > = P(k) delta _Dirac(k + k'). It is worth noting that kappa depends explicitly on Omega ₀ and not only delta because the amplitude of the convergence depends on the projected mass, not only on the projected mass density contrast.

The dependence of the angular power spectrum of the distortion as a function of ( Omega , lambda ), of the power spectrum of density fluctuations and of the redshift of sources has been investigated in detail in the linear regime by Bernardeau et al (1997), Kaiser (1998). Bernardeau et al (1997), Nakamura (1997) computed also the dependence of the skewness of the convergence on cosmological parameters, arguing that it is the first moment which directly probes non-linear structures. From perturbation theory and assuming Gaussian fluctuations, the variance, < kappa ( theta )² > , and the skewness, s₃ = < kappa ( theta )³ > / < kappa ( theta )² > ², have the following dependencies with the cosmological quantities:

$\begin{equation} <\kappa(\theta)^2>^{1/2} \approx 10^{-2} \ \sigma_8 \ \Omega_0^{0.75} \ z_s^{0.8} \left({\theta \over 1^o}\right)^{-(n+2)/2} \ , \end{equation}$

(31)

and

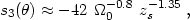$\begin{equation} s_3(\theta) \approx -42 \ \Omega_0^{-0.8} \ z_s^{-1.35} \ , \end{equation}$

(32)

for a fixed source redshift z_s, where n is the spectral index of the power spectrum of density fluctuations and sigma ₈ is the normalization of the power spectrum (the rms mass density fluctuation within a sphere of 8h₁₀₀^-1 Mpc). Hence, since the skewness does not depend on sigma ₈, the amplitude of fluctuations and Omega ₀ can be recovered independently using < kappa ( theta )² > and s₃. The slope of the projected power spectrum can, in principle, be recovered from the complete reconstruction of the projected mass density, using weak-lensing inversion as discussed in Section 3.

Jain & Seljak (1997), generalizing the early work by Miralda-Escudé (1991), have analyzed the effects of non-linear evolution on < kappa ( theta )² > and s₃ using the fully non-linear evolution of the power spectrum (Peacock & Dodds 1996). They found formal relations similar to those found by Bernardeau et al. However, on a scale below 10 arcminutes, < kappa ( theta )² > increases more steeply than the theoretical expectations of the linear theory and is 2 or 3 times higher on scales below 10 arcminutes. These predictions are strengthened by numerical simulations (Jain et al 1998). Therefore, a shear amplitude of about 2-5% is predicted on these scales which should be observed easily with ground-based telescopes (Figure 6). Schneider et al (1998a) recently claimed that they have detected this small-scale cosmic-shear signal.

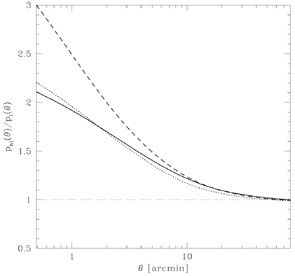Figure 6. Ratio of the amplitude of the polarization predicted by the non-linear and linear evolution of the power spectrum as a function of angular scale (from Jain & Seljak 1997). The normalization is sigma ₈ = 1. The plot shows the expectations for three cosmologies: Omega = 1 (solid line), Omega = 0.3 (dashed line) and Omega = 0.3, lambda = 0.7 (dotted line). The difference between the two regimes becomes significant below the 10' scale.

The previous studies are based on the measurements of ellipticities of individual galaxies in order to recover the stretching produced by linear and non-linear structures. Like the mass reconstruction of clusters, it demands high-quality images and an accurate correction of systematics down to a percent level. An alternative to this strategy has been investigated by Villumsen (1996) who looked at the effect of the magnification bias on the two-point galaxy correlation function. Because the magnification may change the galaxy number density as a function of the slope of the galaxy number counts, it similarly modifies the apparent clustering of the galaxies. From Equations 23 and 25, the two-point correlation function averaged over the directions theta is changed by the magnification of the sources and, in the weak lensing regime, its contribution writes (Kaiser 1992, Villumsen 1996, Moessner & Jain 1998):

$\begin{equation} \omega(\theta)={\left<\left[N_0(m)(5\alpha-2)\kappa(\theta+\theta')\right] \left[N_0(m)(5\alpha-2)\kappa(\theta)\right]\right>\over N_0(m)^2} \ , \end{equation}$

(33)

that is,

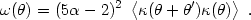$\begin{equation} \omega(\theta)=(5\alpha-2)^2 \ \left<\kappa(\theta+\theta')\kappa(\theta)\right> \ . \end{equation}$

(34)

The galaxy two-point correlation function is therefore sensitive to the correlation function of the convergence and to the slope of galaxy counts. If the unlensed two-point correlation function is known, it is then possible to compute the local correlation function of the convergence from the local two-point correlation function of the galaxies.

Detailed investigations of the capability of this technique have been discussed by Moessner et al (1998) who looked at the effect of non-linear clustering on small scales and for different cosmologies. They raised the point that the correlation function can be also affected by the evolution of galaxies which also modifies the two-point correlation function of galaxies, but in an unknown way. Moessner & Jain (1998) proposed a way to disentangle these two effects by using the cross-correlation of two galaxy samples having different redshift distributions that do not overlap. This minimizes the effect of intrinsic galaxy clustering, but it requires the knowledge of the biasing which can also depend on the redshift. Therefore, the magnification bias method needs auxiliary input that can constrain the biasing independently.