Probing the Universe with Weak Lensing

Annu. Rev. Astron. Astrophys. 1999. 37: 127-189
Copyright © 1999 by Annual Reviews. All rights reserved

4.2. Measuring the Biasing

Because gravitational lensing is directly sensitive to the total mass responsible for the deflection, it provides a potentially important tool for measuring the biasing factor, as it has been demonstrated by the recent weak lensing analysis of the supercluster MS0302+17 (Kaiser et al 1998). In particular, a well-known effect of the magnification bias is the generation of correlations between foreground and background luminous systems observed in catalogues. The matter associated with the foreground systems can amplify the flux received from background objects, which results in an apparent correlation between the number density or the luminosity of backgound objects and the number density of foregrounds (Canizares 1981). The correlation has been first detected by Fugmann (1990) and confirmed later by Bartelmann & Schneider (1993a, b;, 1994) who found correlations of the galaxy number density with the radio-sources of the 1-Jy catalogues, the IRAS catalog, and the X-ray galaxies. Further independent analyses of such associations showed also evidences of magnification bias (Bartelmann et al 1994, Rodrigues-Williams & Hogan 1994, Seitz & Schneider 1995b, Wu & Han 1995, Benítez & Martínez-González 1997, Williams & Irwin 1998). The statistical basis of these associations is surpisingly robust and difficult to explain physically without invoking lensing effects.

Bartelmann et al (1994) argued that the correlation can be interpreted has a magnification bias only if it is produced by condensations of matter, like clusters of galaxies (Bartelmann & Schneider 1993a). In order to check this hypothesis, Fort et al (1996) have attempted to detect weak shear around some selected bright quasars which could be good lensing candidates. They found strong evidence of weak shear around half of their sample with, in addition, a clear detection of galaxy overdensities in the neighborhood of each quasar. The Fort et al sample has been re-analyzed recently by Schneider et al (1998a) and the detection has been strengthened on a more reliable statistical basis, with a firm confirmation for one of the quasars from the HST images obtained by Bower & Smail (1997). In addition, some other observations have also detected gravitational shear around bright radiosources: Bonnet et al (1993) found a shear signal around the double imaged quasar Q2345+007, which was later confirmed to be associated with a distant cluster (Mellier et al 1994;, Fischer et al 1994;, Pelló et al 1996). Similar detection of a cluster has recently been reported around the Cloverleaf (Kneib et al 1998) and around 3C324, which also clearly shows a shear pattern from the HST images (Smail & Dickinson 1995). The sample is nevertheless too small to provide a significant direct evidence that magnification bias is detected in quasar catalogues. Indeed, it would be important to pursue this program using a large sample of bright quasars or radiosources. The field of view does need to be large, so the HST with the Advanced Camera could be a perfect instrument for this project. The impact of such magnification bias could be important for our understanding of the evolution scheme of quasars and galaxies, because it changes the apparent luminosity functions of these samples (Schneider 1992, Zhu & Wu 1997).

If these correlations are caused by magnification bias, a quantitative value of the biasing can in principle be estimated, for instance from the angular foreground-background correlation function (Kaiser 1992), where foreground could be galaxies or dark matter. Bartelmann (1995a) expressed the angular quasar-galaxy correlation, _QG, as a function of the biasing factor, b, and the magnification-mass density contrast cross-correlation function, _µ, in the weak lensing regime:

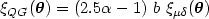$\begin{equation} \xi_{QG}(\thetag)=(2.5 \alpha-1) \ b \ \xi_{\mu\delta}(\thetag) \end{equation}$

(35)

where alpha is the slope of the background galaxy counts. However, since _µ depends on the power spectrum of the projected mass density contrast, the determination of the biasing factor is possible only if one independently obtains the amplitude of the power spectrum. Generalizations to non-linear evolution of the power spectrum and to any cosmology were explored by Dolag & Bartelmann (1997), Sanz et al (1997). As expected, the non-linear condensations increase the correlation on small scales by a very large amount; that, however, still strongly depends on the amplitude of the power spectrum.

With the observation of weak lensing induced by large-scale structures, it becomes possible to observe directly the correlation between the background galaxies and the projected mass density of foreground structures instead of using the light distribution emitted by the foreground galaxies. Following the earlier development by Kaiser (1992), Schneider (1998) has computed the cross-correlation between the projected mass, M, and the galaxy number density of foreground galaxies, N, on a given scale theta , < MN > , as a function of the biasing factor of the foreground structures, b. Like previous studies, it is simply proportional to b, but it also depends on sigma ₈ and the slope of the power spectrum, and as such it is not trivial to estimate it without ambiguity. A more detailed investigation of the interest of < MN > has been done by Van Waerbeke (1998a) who computed the ratio, R( theta ) of the density-shear correlation over the two-point galaxy correlation function for a narrow redshift distribution of foregrounds and a narrow range in scale (Van Waerbeke 1998a, b):

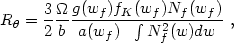$\begin{equation} R_{\theta}={3 \over 2}{\Omega \over b}{g(w_f) f_K(w_f)N_f(w_f) \over a(w_f) \ \ \int N^2_f(w) dw} \ , \end{equation}$

(36)

where a is the expansion factor, w_f is the comoving distance of the foreground, f_K is the comoving angular diameter distance, N_f is the redshift distribution of the foreground galaxies, and

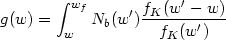$\begin{equation} g(w)=\int_{w}^{w_{f}} N_b(w') {f_K(w'-w) \over f_K(w')} \end{equation}$

(37)

N_b(w') being the redshift distribution of the background galaxies. Using this ratio, he investigated the scale dependence of the biasing, including the non-linear spectrum and different cosmologies, and discussed how it can be used to analyze the evolution of the biasing with redshift, if two different populations of foregrounds are observed. The ratio R / R_' permits one to compare the biasing on two different scales. This quantity does not depend on Omega , on the power spectrum or on the smoothing scale, so it is a direct estimate of the evolution of biasing with scale. Van Waerbeke predicts that a variation of 20% of the bias on scales between 1' and 10' will be detectable on a survey covering 25 square degrees. This ratio is therefore a promising estimator of the scale dependence of the biasing.

The analysis discussed above indicates the potential interest of lensing to the study of the evolution of bias with scale and redshift of foreground, with the direct use of the correlation between the ellipticity distribution of background sources and the projected mass density inferred from mass reconstruction. It thus permits an accurate and direct study of the biasing and its evolution with lookback time and possibly with scale. However, it is worth stressing that Van Waerbeke (like Bartelmann 1995a and others) assumed a linear biasing. In the future it will be important to explore in detail the generalization to a non-linear bias (Van Waerbeke, private communication) as described by Dekel & Lahav (1998).