Copyright © 1997 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1997. 35:
101-136 Copyright © 1997 by Annual Reviews. All rights reserved |
2.2. The Classical Malmquist Bias
In his work, "A study of the stars of spectral type A," Malmquist (1920) investigated how to derive the luminosity function of stars from their proper motions, provided that it is gaussian and one knows the distribution of apparent magnitudes up to some limiting magnitude. This led Malmquist to investigate the question of what is the average value (and other moments) of the quantity R, or the reduced distance, as earlier introduced by Charlier:
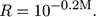 |
(2) |
Malmquist made three assumptions: 1. There
is no absorption in space. 2. The frequency function of the absolute
magnitudes is gaussian (Mo,
 ). 3. This function is
the same at all distances. The third assumption is the principle of
uniformity as implied in
Lundmark's (1946)
definition of distance indicators.
). 3. This function is
the same at all distances. The third assumption is the principle of
uniformity as implied in
Lundmark's (1946)
definition of distance indicators.
Using the fundamental equation of stellar statistics, Malmquist derived
<Rn> and showed that it may be expressed in
terms of the luminosity function constants Mo and
 and the distribution
a(m) of apparent magnitudes, connected with the stellar space
density law. Especially interesting for Malmquist was the case n
= -1,
or the mean value of the "reduced parallax," that appears in the analysis
of proper motions. However, for distance determination, the case n
= 1 is relevant because it allows one to calculate, from the mean value of
the reduced distance, the average value of the distance <r> for
the stars that have their apparent magnitude in the range m ± 1/2
dm or their distance modulus µ = m - Mo in
the range µ ± 1/2 dµ. The result is,
written here directly in terms of the distance modulus distribution
N(µ) instead of a(m),
and the distribution
a(m) of apparent magnitudes, connected with the stellar space
density law. Especially interesting for Malmquist was the case n
= -1,
or the mean value of the "reduced parallax," that appears in the analysis
of proper motions. However, for distance determination, the case n
= 1 is relevant because it allows one to calculate, from the mean value of
the reduced distance, the average value of the distance <r> for
the stars that have their apparent magnitude in the range m ± 1/2
dm or their distance modulus µ = m - Mo in
the range µ ± 1/2 dµ. The result is,
written here directly in terms of the distance modulus distribution
N(µ) instead of a(m),
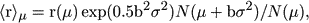 |
(3) |
where b = 0.2 . ln 10. This equation is encountered in connection with the general Malmquist correction in Section 6. Naturally, in Malmquist's paper one also finds his formula for the mean value of M for a given apparent magnitude m:
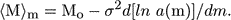 |
(4) |
The term including the distribution of apparent
magnitudes (or distance moduli in Equation 3) reduces to a simple form when
one assumes that the space density distribution d(r)
 r:
r:
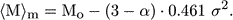 |
(5) |
With  = 0, one finally
obtains the celebrated Malmquist's formula valid for a uniform space
distribution:
= 0, one finally
obtains the celebrated Malmquist's formula valid for a uniform space
distribution:
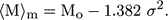 |
(6) |
Hubble (1936) used Malmquist's formula (Equation 6) when, from the brightest stars of field galaxies (and from the magnitudes of those galaxies), he derived the value of the Hubble constant. Hubble derived from a local calibrator sample the average (volume-limited) absolute photographic magnitude and its dispersion for the brightest stars. As "the large-scale distribution of nebulae and, consequently, of brightest stars is approximately uniform," he derived the expected value for the mean absolute magnitude of the brightest stars <Ms> for a fixed apparent magnitude. His field galaxies were selected, Hubble maintained, on the basis of the apparent magnitudes of the brightest stars, which justified the calculation and use of <s>. In the end, he compared the mean apparent magnitudes of the brightest stars in the sample galaxies with <Ms>, calculated the average distance <r>, and derived the value of the Hubble constant (526 km/s/Mpc). Hence, it is important to recognize that this old value of Ho, canonical for some time, already includes an attempt to correct for the Malmquist bias. Also, it illustrates the role of assumptions in this type of correction (what is the space density law, what is the mode of selection of the sample, etc).