Copyright © 1997 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1997. 35:
101-136 Copyright © 1997 by Annual Reviews. All rights reserved |
Of course, this is not a proper place to write a history of selection biases, or how they have been invented and reinvented, considered, or neglected in astronomical works of the present century. However, it seems helpful to introduce the reader to the current discussion of this subject by picking from the past a few important fragments.
2.1. Kapteyn's Problem I and Problem II
In a paper on the parallaxes of helium stars "together with considerations on the parallax of stars in general," Kapteyn (1914) discussed the problem of how to derive the distance to a stellar cluster, presuming that the absolute magnitudes of the stars are normally distributed around a mean value. He came upon this question after noting that for faint stars the progress of getting kinematical parallaxes is slow and "can extend our knowledge to but a small fraction of the whole universe." A lot of magnitude data exist for faint stars, but how to put them to use? He formulated Problem I as follows:
Of a group of early B stars, all at practically the same distance from the sun, we have given the average apparent magnitude <m> of all the members brighter than mo. What is the parallax
of the group?
Changing a little notation and terminology, Kapteyn's answer to this question may be written as an integral equation, where the unknown distance modulus µ appears:
 |
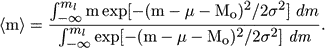(1) |
Because values for the parameters Mo and
of the gaussian
luminosity function are known, one may solve the distance modulus
µ. Note that the integration over apparent magnitudes is
made from -
to
ml, the limiting magnitude. Kapteyn calculated a table
for practical use of his equation, so that from the observed value of
<m>, one gets the distance modulus µ. If one simply
uses the mean absolute magnitude Mo and calculates the
distance modulus as <m> - Mo,
a too-short distance is obtained. Though Kapteyn did not discuss explicitly
this bias, his method was clearly concerned with the Malmquist bias of the
second kind, a typical problem in photometric distance determinations (see
Section 3).
Kapteyn recognized that the situation is different if stars are scattered at varying distances, leading to his Problem II:
Of a group of early B stars, ranging over a wide interval of distance, given the average apparent magnitude of all the stars brighter than mo we require the average parallax of the group.
In this scenario, if one now uses Kapteyn's table mentioned above, taking the µ corresponding to <m>, one generally obtains an incorrect average distance modulus <m>. Also, as in Problem I, one cannot take <µ> = <m> - Mo, either. This Kapteyn's problem (for which he did not offer a complete solution) is related to what is called the classical Malmquist bias.
In Problem I, one has information on relative distances; in this particular case the distances are equal. The necessity of having relative distances indicates that the solution to Problem I is not applicable to a "group" of one star. In Problem II there is no a priori information on relative distances. On the other hand, in order to calculate a mean distance modulus, one needs such information as must be extracted from the only data available, i.e. from the distribution of apparent magnitudes. Again, a sample of a single star with m = mo cannot be a basis for solving Problem II (as an answer to the question "what is the most probable distance of this star?"), unless one makes some assumption on how the magnitudes of the other stars are distributed.