Annu. Rev. Astron. Astrophys. 1997. 35: 101-136 Copyright © 1997 by Annual Reviews. All rights reserved

3.2. Situations Where the First or General Malmquist Bias Appears

Let us consider a class of galaxies having a gaussian luminosity function G(M_p, ) acting in the role of a standard candle. Such a class may be defined, e.g. via a fixed value of the TF parameter p = log V_max, and it is assumed that the calibration has been made, i.e. the volume-limited value of M_p is known. A sample of these galaxies with magnitudes measured up to some limit gives us a collection of derived distance moduli µ = m - M_p. If in addition the redshifts are available, one may construct the µ-log V Hubble diagram, and try to determine the Hubble constant H from the following expected relation:

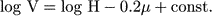(7)

If the error in the distance modulus has a gaussian distribution G(0, ), one can take simple averages <log V> and <µ>, and solve for <log H>. In reality, there is a systematic error in each subaverage <µ_i> (µ_i = constant) and this systematic error generally depends on the value of µ_i if the space distribution of galaxies is not uniform. The error µ(µ_i) is given by Malmquist's formula (Equation 3). One point should be especially emphasized: The ratio N(µ + b²) / N(µ) refers to the distance moduli in the ideal case when the sample is not influenced by a magnitude limit, i.e. when N(µ) contains information on the real space distribution of the galaxies.

One implication of the general Malmquist bias is that the Hubble diagram does not necessarily show a linear Hubble law, because the bias depends on the real distribution of galaxies and is different for different (derived) distances. Also, in different directions of the sky, one may derive by the mentioned method different values of the Hubble constant, possibly interpreted, but incorrectly, to be caused by our own peculiar motion or by large scale streams of galaxies. Such explanations have been applied to the Rubin-Ford effect (Sandage & Tammann 1975a, b, Fall & Jones 1976, James et al 1991), the supergalactic anisotropy (Teerikorpi & Jaakkola 1977), and the Great Attractor velocity field (Landy & Szalay 1992).

The general Malmquist correction has in recent years been discussed particularly in connection with the attempts to derive maps of peculiar velocities or galaxy streams. The radial component of a peculiar velocity for a galaxy with true distance r and observed correct radial velocity V_obs is as follows:

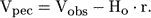(8)

Let us look at galaxies in some direction, with their derived distances within a narrow range r_der ± 1/2 dr. Perhaps these galaxies are also in the real space so close by that they have a common peculiar velocity (bulk flow or stream), though different cosmological components. Then <V_obs> - H_o ^. <r_der> does not give the correct peculiar velocity, unless a proper correction for <r_der> is made, i.e. the Malmquist correction of the first kind, which gives the correct average distance for the galaxies in the r_der ± 1/2 dr range.

Lynden-Bell et al (1988) used such a correction in their Great Attractor paper, though they assumed a uniform distribution of galaxies. This means that for their diameter (vs velocity dispersion) indicator for elliptical galaxies, the bias formula is analogous to the classical Malmquist formula:

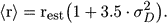(9)