Annu. Rev. Astron. Astrophys. 1996. 34: 461-510 Copyright © 1996 by Annual Reviews. All rights reserved

2. THE STELLAR EVOLUTION CLOCK

Iben & Renzini (1984), Iben (1991) have written fine reviews of our understanding of the evolution of low-mass stars, and Renzini & Fusi Pecci (1988) have carried out an equally valuable analysis of the degree to which canonical stellar evolutionary sequences satisfy the constraints provided by GC color-magnitude diagrams (CMDs). These papers are well worth reading again: Much of what they contain (which is not repeated here) serves to bolster one's confidence in the adequacy and accuracy of computed stellar models. Although many aspects of the more evolved stages of stars remain problematic, the overall picture of stellar evolution is certainly correct. The main point to stress in this section is that the dependence of the turnoff luminosity, L^TO, on age - which constitutes the stellar evolution clock - appears to be an especially robust prediction. (The turnoff is defined to be the hottest point along an isochrone, marking the end of the main-sequence stage and the beginning of the subgiant phase.)

2.1. Uncertainty in L^TO Due to Basic Stellar Physics Inputs

Chaboyer (1995) has recently used the direct approach to ascertain the impact of changes to the basic input physics on GC ages, i.e. he has determined how derived ages would be affected if the nuclear reaction rates, opacities, etc were varied, in turn, by amounts equal to reasonable estimates of their probable errors. Consequently, we use a more indirect means to show, just as Chaboyer has concluded, that present uncertainties in these physical inputs can be expected to have only very minor effects on the ages that are obtained from turnoff luminosities. Our modus operandi reveals, in addition, some of the differences between modern evolutionary calculations and those carried out at earlier times.

2.1.1. NUCLEAR REACTIONS AND OPACITIES    Figure 1 shows plots of the M_bol (TO) [= 4.72 - 2.5 log (L^TO / L)] versus age relationships that have been derived by a number of researchers over the past 25 years. All of the calculations are based on the assumptions that Y = 0.20 and Z = 0.0001 for the mass fraction abundances of helium and the metals, respectively. (Throughout our examination of absolute GC ages, we concentrate on the low-metallicity systems, which are likely to be the oldest.) The locus attributed to Iben (1971) is based on an analytic expression contained therein, which provides a good approximation to the computations by Iben & Rood (1970), Simoda & Iben (1970). The latter assume pre-1966 nuclear reaction rates, for the most part, along with the Hubbard & Lampe (1969) set of conductive opacities and the Cox & Stewart (1970) radiative opacity data. Very similar input physics was used in the extensive grid of evolutionary tracks computed by Mengel et al (1979), which were the basis of the Ciardullo & Demarque (1977) isochrones. These were subsequently revised by Green, Demarque & King (1987) to make them better represent real stars. To be specific, the original Yale isochrones were shifted in effective temperature (T_eff) to compensate for the fact that Mengel et al tracks were computed for the choice of _MLT = 1.0 instead of the more realistic value of 1.5. [The quantity _MLT is an adjustable parameter in the mixing-length theory (MLT) of convection, which is commonly used in the construction of stellar evolutionary sequences.] Hence both sets of isochrones predict the same dependence of M_bol(TO) on age (the dotted curve in Figure 1).

Figure 1. Turnoff luminosity vs age relations from the indicated investigations for the particular choice of Y = 0.20 and Z = 0.0001 for the mass-fraction abundances of helium and the heavier elements, respectively. The Mbol(TO) values were calculated on the assumption that the solar value is 4.72 mag. Small amounts of smoothing were applied in some instances. The differences between the various loci are discussed in the text.

VandenBerg & Bell (1985) adopted the updated nuclear reaction rates given by Harris et al (1983) and opacities derived from the Los Alamos Astrophysical Opacity Library (Huebner et al 1977). They noted that revisions to the nuclear physics had a ~ 2% effect on the calculated age-luminosity relation for a given evolutionary track. Because, at low Z, opacities are completely dominated by the free-free transitions of H and He (cf Schwarzschild 1958), the ramifications of improved determinations of the metal contribution are simply not significant. For instance, the use of the even more modern OPAL opacities (Rogers & Iglesias 1992), which is the main difference between the dashed curve in Figure 1 and the VandenBerg-Bell results, yields essentially the same relation between M_bol(TO) and age. Indeed, the insensitivity of such relations to the particular generation of opacities assumed gives one considerable confidence in the predictions for, especially, the most metal-poor stars. But, even at higher Z, turnoff luminosity versus age relations are affected much less by improvements to the opacity than, say, the mass-luminosity relation for zero-age main-sequence stars (e.g. see Figure 4 in VandenBerg & Laskarides 1987). Although enhanced opacities will increase the main-sequence lifetime of a fixed mass, metal-rich star, they will also decrease the turnoff luminosity, such that nearly the same relationship between L^TO and age is obtained (Rood 1972, VandenBerg 1983). Fortunately, there is good reason for believing that current opacities are uncertain by no more than ± 10-20%, given that the OPAL data have led to the resolution of several longstanding discrepancies between the predictions of stellar models and actual observations (see the review by Rogers & Iglesias 1994).

2.1.2. EQUATION OF STATE    The three lowermost curves in Figure 1 differ from the others in one important respect: They allow for Coulomb interactions in the equation of state. Proffitt (1993) was the first to show that this nonideal gas effect causes an 4% reduction in age at a given turnoff luminosity for stellar masses and chemical compositions appropriate to the globular clusters. This is close to the difference between the dashed and solid curves, which represent otherwise identical calculations except that the former ignores, and the latter includes, a Coulomb correction term in the free energy. Particularly noteworthy are the Chaboyer & Kim (1995) results: These authors used (in tabular form) the OPAL equation of state (Rogers 1994), which treats several other nonideal effects. They found a 6-7% reduction in age at a given M_bol(TO), compared with the case when using the ideal gas law with radiation pressure and electron degeneracy assumed. [Their findings agree well with those of VandenBerg et al (1996) (see Figure 1), whose equation of state was set up to provide a good approximation of the more general OPAL code.]

Judging from the difference (in Figure 1) between the Iben (1971) and the Chaboyer & Kim (1995) results, there has been about a 15% reduction in the predicted age at a fixed M_bol(TO) over the past 25 years (for the chemical composition that we have been considering). This reduction has resulted from steady refinements in the nuclear reaction rates, opacities, and equation of state during this time. These aspects of stellar physics are now believed to be sufficiently well understood that future developments in these areas are unlikely to affect predicted ages at more than the few percent level. This conclusion has also been reached by Chaboyer (1995), whose paper contains a useful table giving the fractional age errors as a function of the input physics (also see Renzini 1991).

2.1.3. CONVECTION THEORY    A more serious concern may be the mixing-length theory of convection. Chaboyer's (1995) calculations show that, although the predicted age-luminosity relation for a given track is not greatly affected by changes in _MLT, the age-color (or, equivalently, the luminosity-color) relation is altered in such a way as to shift significantly the luminosity of the hottest point on the track. This is quite an unexpected result. However, while previous studies (e.g. Demarque 1968, VandenBerg 1983) have shown that different assumptions about _MLT have profound implications for the temperature scale of an evolutionary track, without affecting its turnoff luminosity, it has apparently not been checked that the turnoffs of isochrones are similarly independent of _MLT. In fact, Chaboyer has shown that this is not the case. This is perhaps not too surprising given that the temperature shift induced by a change in _MLT is a nonlinear function of mass and evolutionary state (see Figure 3 in VandenBerg 1983).

From a consideration of isochrones computed for values of _MLT in the range of 1.0 to 3.0, Chaboyer (1995) has surmised that uncertainties in how to treat convection lead to about a 10% uncertainty in GC ages as inferred from the turnoff luminosity. This is arguably a very generous error estimate given that there is no compelling evidence at the present time to suggest that _MLT differs by a large factor between stars of different mass or chemical composition or that it depends sensitively on evolutionary state. Rather, the present observational indications are that the value of _MLT needed to produce a realistic solar model is very similar to (possibly even the same as) that needed to explain the lower main-sequence slopes of young open clusters on the CMD (VandenBerg & Bridges 1984), to fit the CMD positions of the local Population II subdwarfs (see Section 3.1 in the present study; VandenBerg 1988), to match the properties of well-observed binaries whose components are in widely separated evolutionary phases (Andersen et al 1988, Fekel 1991), and to reproduce the effective temperatures of GC giant branches as determined by Frogel, Persson & Cohen (1981) from V - K photometry (Straniero & Chieffi 1991, VandenBerg et al 1996). The last of these is potentially one of the most powerful constraints since the predicted position of the giant branch is highly dependent on the choice of _MLT and the comparison between theory and observation is largely independent of the GC distance scale (because the giant branch rises so vertically and its position varies only slightly with age). Frogel et al (1981) suggest that the uncertainty in their inferred temperatures is ± 90 K; even if the error were as large as ± 150 K, this could be accommodated by adopting a value of _MLT that differs by as little as ± 0.3 (see VandenBerg 1983).

The value of _MLT cannot be constrained any better than this, given the current observational uncertainties and the sensitivity of model temperatures to many other factors besides convection theory - notably the low-temperature opacities and the treatment of the model atmosphere boundary condition (see VandenBerg 1991). For this reason, the recent suggestion by Chieffi, Straniero & Salaris (1995) that _MLT appears to be a weak function of metallicity is not convincing. Their fits to GC giant branches on the M_bol - logT_eff plane required a value of _MLT = 1.91 ± 0.05 for clusters of intermediate metal abundance (Z 0.001), whereas the slightly smaller value, 1.75 ± 0.1, was needed for the globulars having Z 0.0001. Obviously, such a small variation is well within the noise of its determination. One is instead impressed (once again) by the fact that stellar models are able to reproduce the observed properties of very different stars with little (or no) variation in _MLT. It would be an astonishing result if _MLT were constant, because there is no reason whatsoever why it should be; however, what variation there is in this parameter appears to be quite small.

The Chaboyer (1995) investigation does, however, raise the specter that a more realistic theory for convection than the MLT may have significant ramifications for GC ages. This possibility has been given considerable impetus by Mazzitelli, D'Antona & Caloi (1995), who have found that the predicted ages of the most metal-poor GCs are reduced by ~ 2 Gyr simply as a consequence of replacing the MLT by the Canuto & Mazzitelli (1991, 1992; hereafter CM) theory of turbulent convection. This theory, unlike the MLT, allows for a full spectrum of turbulent eddies, and it has essentially no free parameters: The mixing length is taken, at any point in the convective envelope, to be the geometrical depth from the upper boundary of the convection zone. [This choice for the scale length is claimed to be reasonable on the grounds of physical analogies (e.g. with the Earth's atmosphere) and its consistency with the physical scale length at which the superadiabatic zones inside stars grow and fade. Indeed, from the observed p-mode solar oscillation frequencies, Basu & Antia (1994) have found that envelope models based on the CM formalism provide a much closer match to the inferred structure of the Sun's convection zone than those constructed assuming the MLT. More recent developments (see Rosenthal et al 1995), however, suggest that this agreement may not necessarily imply such a clear-cut preference for the CM theory over the MLT.]

Mazzitelli et al (1995) find that T _eff effects alone lead to an apparent decrease in the turnoff luminosities of CM isochrones relative to those obtained using the MLT. (A representative example of their results is illustrated in Figure 2 for an assumed metallicity Z = 10^-4.) They verified that the temporal variation of luminosity and central hydrogen abundance along an evolutionary track is independent of how surface convection is treated (as it should be), concluding that it is the differences in morphology of the CM tracks that give rise to the decrease in M_bol(TO) in the corresponding isochrones, compared with MLT predictions. However, an age estimate based strictly on the turnoff luminosity will necessarily have a large uncertainty (in addition to those arising from, e.g. distance or chemical composition errors) because of the inherent difficulty in determining that point. By definition, an observed color-magnitude diagram is vertical at the turnoff; consequently, random photometric scatter or small systematic errors in the color calibration can easily cause the estimated magnitude of the bluest point to be in error by 0.1 mag (if not more) - thereby changing the derived age by at least 10%. But this uncertainty can be significantly reduced if, once the cluster distance is set using one or more standard candles (see Section 3), theoretical isochrones for the applicable chemical abundances are shifted horizontally (i.e. in color) by whatever amount is necessary to obtain a best-fit to the main-sequence photometry, and then the age is inferred from the coincidence of the predicted and observed subgiant-branch loci. The level of the subgiant branch (say, midway between the turnoff and the base of the RGB) is clearly a much better luminosity diagnostic than the turnoff point and, moreover, it is insensitive to the choice of convection theory (see Figure 2). (Granted, in the case of models that employ the MLT, large variations in _MLT would have some impact on the location/shape of the subgiant branch, but the value of this parameter appears to be fairly well constrained.) The treatment of convection need not, therefore, be a serious concern for the determination of GC ages.

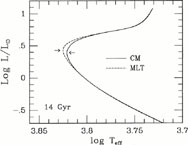Figure 2. Comparison of Mazzitelli et al (1995) isochrones for Z = 0.0001, an age of 14 Gyr, and two different treatments of convection (see text). To obtain a superposition of the main-sequence loci, the MLT predictions were shifted by - 0.0025 in logTeff. Arrows indicate the turnoff points.