Annu. Rev. Astron. Astrophys. 1996. 34: 461-510 Copyright © 1996 by Annual Reviews. All rights reserved

2.2. Uncertainty in L^TO Due to Additional Physics Usually ignored

There are (at least) three additional physical processes that can potentially influence the estimated ages of globular cluster stars: 1. atomic diffusion (or gravitational settling), 2. rotation, and 3. mass loss.

2.2.1. ATOMIC DIFFUSION    Noerdlinger & Arigo (1980) were the first to construct models for low-mass, Population II stars in which helium was allowed to settle under the influence of gravity and thermal diffusion. They found that He diffusion tends to speed up a star's main-sequence evolution, with the result that the evolutionary tracks had slightly lower turnoff luminosities and effective temperatures compared with their nondiffusive counterparts. This translated into about a 22% reduction in the estimated ages of the globulars if the turnoff luminosity were used as the sole criterion for determining age. The follow-up study by Stringfellow et al (1983) added the interesting result that, as stars ascend the red-giant branch (RGB), the remixing of the outer layers by the deepening envelope convection erases much of the evidence of the settling of helium, and the tracks with and without diffusion gradually converge.

Nearly a decade later, Proffitt & Michaud (1991) computed a new set of diffusive models for metal-poor dwarfs using the improvements to the input physics that had occurred in the meantime - mainly to the diffusion coefficients (Paquette et al 1986). The turnoff luminosities of these models appeared to be significantly less affected by diffusion than the earlier calculations had predicted. And, in fact, the isochrones computed shortly thereafter by Proffitt & VandenBerg (1991) and by Chaboyer, Sarajedini & Demarque (1992) revealed that the age at a given L^TO is reduced by 10% due to the gravitational settling of helium. [These investigations also suggested that the impact of diffusion on cluster ages would be appreciably less than this if the latter were obtained from a calibration of the magnitude difference between the horizontal branch and the turnoff. Somewhat reduced HB luminosities, compensating for 1/2 of the decrease in L^TO, is the expected consequence of differences in the envelope helium contents in the precursor red giants: Not all of the helium that had previously settled below the surface convection zone is dredged back up when the convection attains its deepest penetration on the lower RGB. Hence the envelopes of stars in more advanced evolutionary stages will be characterized by lower Y, which has the stated effect on HB luminosities (see, e.g. Sweigart & Gross 1976).]

However, atomic diffusion is not without its difficulties. As shown by, e.g. Michaud, Fontaine & Beaudet (1984), Chaboyer & Demarque (1994), stellar models that allow for diffusion appear to be unable to explain the lithium abundance plateau (Spite & Spite 1982), which is the near constancy of Li abundance in halo stars having T_eff > 5500 K (see, as well, Thorburn 1994). They also yield isochrones that are morphologically distinct from observed globular cluster CMDs (Proffitt & VandenBerg 1991). In contrast, the same investigations show that such data can be matched extremely well by standard, nondiffusive calculations. (The shapes of isochrones are altered by diffusion because it causes a rapid settling of helium in the very metal-poor stars, in particular, from the thin surface convection zones that they possess during their main-sequence phases. This leads to reduced turnoff temperatures by 200-300 K, whereas, as already mentioned, giant-branch effective temperatures remain relatively unaffected. One must always be wary of drawing strong conclusions from T_eff / color comparisons, but it seems unlikely that current estimates of the temperatures of turnoff stars are uncertain by much more than ± 100 K.)

Why, then, is diffusion so problematic for Population II stars when it is not for, e.g. the Sun? Indeed, helioseismic data indicate a clear preference for solar models that include its effects (see Guzik & Cox 1992, 1993, Christensen-Dalsgaard, Proffitt & Thompson 1993). Because diffusion is such a fundamental physical process, which should occur in all stars, one can only conclude that something must be inhibiting its importance in metal-deficient stars. Suggested possibilities include turbulence (Proffitt & Michaud 1991), rotation (Chaboyer & Demarque 1994), and mass loss at the level of 10^-12 M yr^-1 (Swenson 1995). Turbulent mixing below the surface convection zone will slow the rate at which the surface He abundance decreases, but as demonstated by Proffitt & Michaud (1991), it cannot eliminate the gravitational settling of helium without destroying more lithium than is consistent with the Spite plateau. The combined rotation-diffusion models of Chaboyer & Demarque (1994) are able to match the Li observations reasonably well, but they predict essentially the same evolutionary tracks on the H-R diagram as the pure diffusion calculations; consequently, the T_eff scale problems noted above would remain. Finally, Swenson's (1995) work has revealed that stellar models that treat diffusion can be made compatible with the Li data, and possibly even with globular cluster CMDs, if mass loss is assumed to occur at modest rates during main-sequence evolution.

Although stellar models that include these additional processes, which must operate to some extent in real stars, do not satisfy the observational constraints quite as well as one would hope, they do go a considerable distance towards overcoming the initial objections to diffusion. It is entirely possible that improved treatments of turbulence, rotation, and/or mass loss will reduce the remaining discrepancies concerning the surface properties of Population II stars, but they would not affect the shortening of main-sequence lifetimes due to He diffusing into the stellar cores (unless rapid core rotation could do so). Accordingly, in our view, there is really very little basis for ignoring the implications of diffusion for GC ages, which amount to less than a 10% reduction in age at a given turnoff luminosity. [This value may be slightly revised when models for GC stars become available that allow for the settling of heavier elements such as C and Fe, whose diffusion velocities are comparable with that of helium (Michaud et al 1984). Proffitt's (1994) latest solar models indicate that heavy-element settling causes only minor structural changes beyond those arising from He diffusion alone.]

2.2.2. ROTATION    Rotation clearly has considerable potential in its own right to alter stellar ages (cf Law 1981), and given the abundance of direct and circumstantial evidence for rotation in GC stars, one might surmise that it has a significant impact on the ages of these objects. From the broadened lines evident in echelle spectra, Peterson (1985a, b) determined that the blue HB stars in a number of GCs rotate at significant rates (typical vsin i values of ~ 10-20 km s^-1). Moreover, she found that the mean rotation speeds were directly correlated with the ratio B / (B + R), where B represents the number of HB stars to the blue of the instability strip and R denotes the number to the red. That is, the bluer a cluster's horizontal branch, the faster its stars rotate, on average. A qualitatively similar correlation exists between the apparent cluster ellipticity and HB type (Norris 1983): None of the most highly flattened globulars has a red horizontal branch. Although the ellipticity is presumably a reflection of the total cluster angular momentum, the Peterson data suggest that it may also be indicative of the amount of rotational angular momentum contained within individual member stars. Nonetheless, the Peterson observations do provide some support for those suggestions (e.g. by Fusi Pecci & Renzini 1975, Renzini 1977) that rotation could be a significant factor in determining the morphology of the horizontal branch. Importantly, they also show that at least some GC stars are able to retain substantial amounts of angular momentum in their interiors throughout their evolutionary histories.

Another possible signature of rotation is the observed spread in color / T_eff encompassed by a globular cluster's HB population. Such data seem to require that there is a large variation in mass among the core He-burning stars and that their mean mass is significantly smaller than that of stars presently near the turnoff (cf Rood 1973). Variable amounts of mass loss, driven (perhaps) by star-to-star differences in rotation rate, must therefore occur either during the giant-branch evolution and/or as a consequence of the helium flash event itself.

The huge variations in the measured strengths of the CN, CH, and NH bands, and in the inferred or derived abundances of C, N, and O among bright GC giants (see the review by Kraft 1994 and references therein) provide further indirect evidence for the presence of rotation. These variations are not predicted by canonical evolutionary theory, but are plausibly explained in terms of circulation currents spawned by rotation (Sweigart & Mengel 1979, Smith & Tout 1992); or they may arise as the result of thermal instabilities in the H-burning shell (see Schwarzschild & Härm 1965, Von Rudloff, VandenBerg & Hartwick 1988). Especially compelling are those observations that show a dependence of molecular band strengths on giant-branch luminosity. For instance, as shown in Figure 3, the mean C abundance in M92 stars appears to decline continuously with advancing evolutionary state: Very similar trends have been observed in M15 (Trefzger et al 1983) and in NGC 6397 (Briley et al 1990). The data that have been plotted exhibit a spread of up to ~ 0.7 dex in [C/Fe] at a given M_V, which could be accounted for if some stars mix more than others due to differences in their angular velocities. ([C/Fe] represents the logarithm of the C/Fe number abundance ratio in an observed star minus the logarithm of the same quantity in the Sun, e.g. [C/Fe] = -1 means that the measured carbon-to-iron ratio is one tenth of the solar value.) Low (or super-low) oxygen abundances are also being found in the same GCs - see Pilachowski (1988), Sneden et al (1991), Bell, Briley & Norris (1992) regarding M92, M15 and M92, and NGC 6397, respectively - as well as in M13 (Brown, Wallerstein & Oke 1991, Kraft et al 1993). The critical point is that nitrogen tends to be anticorrelated with C and O, often (though probably not always) to the extent that C+N+O is a constant (see Pilachowski 1989). This strongly suggests that the envelopes of bright giants in many globular clusters are somehow connected to the nuclear burning shell regions and are experiencing ongoing C N and O N processing. Indeed, ad hoc simulations that extend and maintain convective mixing down to the vicinity of the H-burning shell appear to be able to reproduce the observed abundance trends (see VandenBerg & Smith 1988).

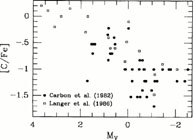Figure 3. Carbon abundance as a function of MV in M92. Only those data not flagged as being uncertain in the indicated studies, from which the observations were obtained, have been plotted.

The hypothesis that rotationally induced deep mixing is responsible for "anomalous" abundances in GC giants has become more credible during the past couple of years. Such mixing might also explain the correlations between, e.g. the strengths of sodium and aluminum lines with that of the CN band (Peterson 1980), which have been particularly difficult to fathom. It was generally supposed (cf Cottrell & Da Costa 1981) that such data indicated the existence of primordial abundance fluctuations, which is to say that the gas out of which the cluster stars formed was not well-mixed chemically. But a separate explanation for these anomalies may not be needed. Furthering the work of Denisenkov & Denisenkova (1990), who first explored the possibility that ²²Ne(p, )²³Na operated at the same temperatures as O N burning, Langer, Hoffman & Sneden (1993) showed that deep mixing to this region of a star would naturally produce an N-Na correlation. In addition, they pointed out that the rate of ²⁵Mg(p, )²⁶Al was essentially the same as that of the aforementioned reaction and hence that, as long as ²²Ne and ²⁵Mg were present, the production of nitrogen by O N cycling would be accompanied by the production of ²³Na and ²⁶Al. Because this occurred at a somewhat cooler temperature than the location of the H-burning shell, mixing into this region would not supply additional fuel into the hydrogen shell and would not, therefore, alter stellar evolution lifetimes.

Thus, a reasonably satisfactory explanation could be offered for the many observations revealing large overabundances of Na and Al, N-Na and N-Al correlations, and O-Na and O-Al anticorrelations (e.g. Cohen 1978, Norris & Freeman 1983, Paltoglou & Norris 1989, Pilachowski 1989, Lehnert, Bell & Cohen 1991, Drake, Smith & Suntzeff 1992, Kraft et al 1992). The main point of disagreement concerned the Langer et al (1993) prediction that the range in Al abundances should be [Al/Fe] 0.3, whereas the observed variation can be as high as [Al/Fe] ~ 1.2 (also see Norris & Da Costa 1995). But with even deeper mixing, and with large initial abundances of the ^25,26Mg seed nuclei [the ²⁶Mg(p, )²⁷Al reaction can operate at a significant rate just below the O N shell], these data can also be matched by proton-capture nucleosynthesis models (Langer & Hoffman 1995). These models predict that large aluminum enhancements should be accompanied by observable (~ 0.2 dex) depletions in Mg (initially mostly ²⁴Mg, which does not burn). These depletions may already have been detected: Smaller magnesium abundances appear to distinguish the super-oxygen-poor stars in M13 from those having higher oxygen abundances (MD Shetrone, private communication 1995).

An important consequence of the extra-deep mixing, according to Langer & Hoffman (1995), is that significant depletions of the envelope H abundance (or, equivalently, enhancements in the surface helium abundance) amounting to ~ 3-10% or more would likely occur. This would have some implications for the upper-RGB lifetimes of the affected stars, and it would influence their later evolution. As is well known (cf Rood 1973), higher envelope-helium contents make for hotter and somewhat brighter core He-burning stars. Langer & Hoffman suggest that this may help to explain why M13 has such a blue HB: The bluest stars could be characterized by higher Ys in their envelopes. (Alternatively, or in addition to this, these stars could have been subject to especially severe mass-loss rates.) Curiously, Moehler, Heber & de Boer (1995) find that high helium abundances seem to be necessary to explain the spectra of extremely blue HB stars in M15.

Not surprisingly, there are some concerns. For one, the meridional circulation mechanism should not work prior to the H-burning shell contacting the chemical composition discontinuity that is produced when the envelope convection attains its greatest penetration (near the base of the RGB): The significant mean molecular weight gradient between the energy-producing shell and that discontinuity (see Sweigart & Mengel 1979) should inhibit circulation (Tassoul & Tassoul 1984) until contact between the two is made. This contact should occur near M_V = 0 in very metal-poor stars (VandenBerg 1992), at which point there should be a brief hesitation in the rate of evolution up the giant branch as the H-burning shell adjusts to a higher hydrogen abundance (also see Iben 1968a, Sweigart & Gross 1978). In fact, Fusi Pecci et al (1990) claim to have detected the consequent bump in the RGB luminosity function at very close to this magnitude. Yet the progressive depletion of carbon in, e.g. M92 apparently begins fainter than M_V = 3 (see Figure 3), which would seem to be totally at odds with the theory and the Fusi Pecci et al observation.

This dilemma has yet to be resolved. On the one hand, the RGB bump is a very subtle feature in metal-deficient clusters; indeed, Fusi Pecci et al (1990) had to coadd the data for several of these objects in order to improve the signal-to-noise ratio. On the other hand, the measured C abundances are the least secure for the faintest stars, and perhaps these data are in need of significant revision. One point in favor of the abundance data, though, is that the subgiant and giant branch luminosity functions of [Fe/H] ~ -2 GCs show anomalous features and cannot be adequately matched by standard evolutionary predictions (see Bergbusch 1990, Stetson 1991, Bolte 1994). This point is discussed further in Section 2.5. Clearly, further and better observations are required.

Another concern is that deep mixing cannot be invoked to explain all of the abundance data. In M92, for instance, not all stars with low C abundances are nitrogen rich (Carbon et al 1982). Furthermore, despite the evidence for progressively lower ¹²C / ¹³C ratios with increasing luminosity in some GCs (Smith & Suntzeff 1989), low carbon isotope ratios are often found in CN-normal stars, which have presumably not undergone substantial mixing (Bell, Briley & Smith 1990). Moreover, many clusters show bimodal distributions of CN-band strengths (Smith & Norris 1982; also see the review by Smith 1987), which persist right down to the main-sequence turnoffs in some globular clusters (e.g. 47 Tucanae; see Briley, Hesser & Bell 1991). The all-important point here is that the ratio of CN-strong to CN-weak stars does not appear to change with evolutionary state (Smith & Penny 1989, Smith & Norris 1993, Briley et al 1994). The existence of some level of primordial abundance variations would seem to be the inescapable conclusion.

Several general results bring home the complexity of globular cluster abundance work. First, as already implied, RGB mixing tends to become less severe as the cluster metallicity increases (Bell & Dickens 1980, Briley et al 1992). In metal-poor systems, CNO abundances seem to vary with M_V along much of the giant branch, whereas CN bimodalities with little or no dependence on evolutionary state appear to be characteristic of the more metal-rich globulars. Are we to conclude from this that the mean rotation rates of stars in GCs vary in some systematic way with [Fe/H]? If so, does this impact on derived ages and the age-metallicity relation that describes these objects? Second, even at the same metal abundance, different clusters show a considerable variation in their observed chemistry. Adding to the Suntzeff (1981) study of M3 and M13, which have essentially identical [Fe/H] values, Kraft et al (1992) report that they have been unable to find any super-low-oxygen stars in M3, whereas they comprise ~ 15% of the brightest giants in M13. Furthermore, although M13 stars tend to have low oxygen and high sodium abundances, those in M3 are O rich and Na poor. Do M13 stars rotate more rapidly than those in M3 and is this the reason why the two clusters also exhibit very different horizontal-branch morphologies? And finally, Population II field giants do not show the extreme abundance patterns seen in GC giants. No CN-strong stars are found in the field (Langer, Suntzeff & Kraft 1992), and many have noted the lack of field stars with high [Na/Fe] or [Al/Fe] (e.g. Brown & Wallerstein 1993, Norris & Da Costa 1995). Is it, then, a risky procedure to use field RR Lyraes to determine cluster distances? For that matter, how safe is it to use canonical horizontal-branch models to set the globular cluster distance scale given that the precursor RGB stage is problematic?

It is hard to deny the importance of rotation in GC stars and how it affects their evolution. However, precisely defining and quantifying the role that it plays are not easily accomplished in view of the relatively crude understanding that we presently have of turbulence, circulation, and angular momentum transport in rotating stars (see, e.g. Zahn 1992). Still, exciting progress is being made through such studies as those by Wasserburg, Boothroyd & Sackmann (1995), Charbonnel (1995), who have been able to account for, among other things, the low ¹²C / ¹³C ratios in bright giants by invoking meridional circulation. Further investigations along these lines are strongly encouraged.

But are the rotation rates of stars in clusters sufficient to significantly affect the relation between age and L^TO predicted by standard, nonrotating stellar models? The answer to this question is "probably not." Deliyannis, Demarque & Pinsonneault (1989) have computed a number of evolutionary sequences for low-mass, low-metallicity stars in which internal rotation is followed using the moderately sophisticated code described by Pinsonneault et al (1989). The transport of angular momentum due to rotationally induced instabilities, the angular momentum loss due to a magnetic wind, and the effects of rotation on the chemical abundance profiles are all calculated. In addition, the various free parameters in the theory have been constrained to satisfy the global properties of the Sun, including its present rotation rate and oblateness. Very encouraging is the fact that, as noted by Pinsonneault et al, the predicted rotation in the solar interior is in qualitative agreement with the estimates from oscillation data, especially at radii 0.6 R. The code has proven successful in modeling the observed surface Li abundances and rotation rates of stars in young open clusters (Pinsonneault, Kawaler & Demarque 1990) and in the halo (Pinsonneault, Deliyannis & Demarque 1992).

The calculations of Deliyannis et al (1989) for globular cluster parameters predict that rotation will not change the age at a given turnoff luminosity by more than 1%. Moreover, they suggest that, due to angular momentum redistribution and losses at the stellar surface, the angular momentum of the core is kept at a level that is insufficient to alter canonical estimates of the core mass at the helium flash. As a result, HB luminosities should not be affected nor should calibrations of the age dependence of the magnitude difference between the turnoff and the horizontal branch. At the same time, the models are expected to possess sufficient differential rotation with depth (according to Pinsonneault, Deliyannis & Demarque 1991), to be capable of matching the rotational velocity data that Peterson (1985a, b) has obtained for the HB stars in several GCs. (These inferences are based on the rotational characteristics of turnoff models: As far as we are aware, the tracks have not yet been extended past the lower RGB.) Worth repeating is the comment by Pinsonneault et al that "the thin surface convection zones of halo stars allow differential rotation with depth to begin much further out and to reach a greater contrast between central and surface rotation." This offers the reason why one might expect rotation (and mixing?) to become more important as the cluster metallicity decreases.

All of this represents a really superb theoretical effort and further progress is eagerly anticipated. In particular, it will be interesting to learn whether or not these models can explain the wealth of chemical abundance data previously described. Until those constraints are matched, we suspect that it is still within the realm of possibility that rotation has a bigger effect on turnoff ages than Deliyannis et al (1989) have estimated. However, extremely high rotation rates can be precluded simply because the turnoff stars in GCs follow very tight color-magnitude relationships - see, e.g. Stetson's (1993) review, wherein he reports that M92's photometric sequence is only 0.0078 mag thick in B - V in the range 17.8 < V < 18.4 (which is just above the turnoff). If the stars in clusters had high rotation rates, then much larger intrinsic spreads would be expected because of star-to-star differences in rotational velocity and the dependence of a star's photometry on the particular aspect being viewed (e.g. see Faulkner, Roxburgh & Strittmatter 1968). On the other hand, judging from the very simplistic models by Mengel & Gross (1976), who treat rotation in the spherically symmetric approximation, fairly large rotation rates are needed to cause significant departures from the evolutionary track that a nonrotating star of the same mass and chemical composition would follow. That is, the tightness of observed CMDs does not preclude rotation rates that are large enough to have small effects on the core mass at the helium flash or to change computed age versus turnoff luminosity relations at the few percent level (see the Mengel & Gross study). Note that rotation tends to increase the age at a given L^TO.

2.2.3. MASS LOSS     A few years ago, Willson, Bowen & Struck-Marcell (1987) suggested that significant mass loss ( 10^-9 M yr^-1) may occur in the region of the main sequence that overlaps with the extension of the Cepheid instability strip. This mass loss would be driven by pulsation as well as the rapid rotation normally possessed by the early-A to mid-F stars that occupy this region. They suggested, for instance, that the Sun's very low Li abundance (Steenbock & Holweger 1984) could be explained if it started out as as a 2 M star and lost half its initial mass during the first 10⁹ yr of its existence as it evolved through this critical zone on the H-R diagram. According to Willson et al, this mechanism might also account for blue stragglers, and it may even help to alleviate the apparent conflict between GC ages and the age of the Universe implied by high values of H₀ (should they prove to be correct).

Noting that the instability strip crosses the main sequence very near to where the so-called Li dip ³ occurs in Population I stars of type F, Schramm, Steigman & Dearborn (1990) considered whether or not the Willson et al (1987) hypothesis might also work here. They found that models that lose mass at 7 × 10^-11 M yr^-1 are able to match the shape of the Li dip in the Hyades quite well. However, the mass-loss rate had to be < 1 × 10^-10 M yr^-1 in order to avoid being in conflict with the observation that beryllium is not depleted (Boesgaard & Budge 1989). In their much more extensive study, Swenson & Faulkner (1992) agreed that mass-loss models are capable of matching the Li contents of Hyades F stars, but that very little leeway is allowed in the mass-loss rates, which must vary nonmonotonically with initial stellar mass in a very well-defined way, with little star-to-star deviation. [Note that there are alternative explanations for all or part of the Li-dip observations, including atomic diffusion (Michaud 1986) and rotationally induced mixing (e.g. Charbonnel & Vauclair 1992).]

Based on the existence of a few extremely metal-deficient stars with very low Li abundances, Dearborn, Schramm & Hobbs (1992) suggested that an analogous lithium dip might be present on the Population II main sequence. Further, they found that such data could be explained by the same mass-loss model as was used for the Hyades if mass-loss rates of ~ 10^-11 M yr^-1 were assumed to apply within an instability strip lying in the range 6600 T_eff 6900. They commented that mass loss of this type would make GCs look ~ 1 Gyr older than they really are (also see Shi 1995). However, Molaro & Pasquini (1994) have detected lithium in a turnoff star of the [Fe/H] - 2.1 globular cluster NGC 6397, and, moreover, their measured Li abundance is the same as those of field halo stars (e.g. Thorburn 1994) to within the errors. This observation provides a very strong argument against the high mass-loss hypothesis, especially given that the field star data themselves preclude mass-loss rates 2 × 10^-12 M yr^-1 (Swenson 1995). (It also gives a reassuring indication of the similarity between cluster and field main-sequence stars at low Z.)

As discussed by Shi (1995), there is another way to test whether or not the turnoff stars in GCs are losing significant amounts of mass. If they are, then a step-like feature, reflecting the sudden onset of high mass-loss rates, should manifest itself in the luminosity function plane at the point where the CMD intersects the instability strip. Although there are some anomalous features in the observed luminosity functions for GCs, mainly for the most metal-deficient systems (see Section 2.5), they appear to be restricted to post-turnoff evolutionary phases. That is, no obvious bumps or steps are seen at turnoff luminosities. All in all, the possibility that mass-loss rates are high enough to affect GC ages seems remote.

³ The Li dip refers to the striking variation of Li abundance with T_eff that Boesgaard & Tripicco (1986) discovered in the Hyades: Stars with T_eff's near 6600 K show severe Li depletions compared with those 300 K cooler or hotter. Back.