Annu. Rev. Astron. Astrophys. 1980. 18: 489-535 Copyright © 1980 by Annual Reviews. All rights reserved

(a) Receivers

The receiver sensitivity is often specified in terms of the smallest measurable change in temperature of a Rayleigh-Jeans thermal source that covers the entire antenna aperture, in a post-detection bandwidth of 1 Hz - an integration time of approximately 1/2 second. The minimum detectable temperature change is given by

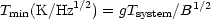(1)

where g is a factor between 1 and 2 determined by the type of modulation and integrating filter. B is the receiver bandwidth determined by the mixer or the intermediate frequency amplifier. The system noise is characterized by T_system, the temperature of a fictitious Rayleigh-Jeans source placed over the antenna aperture that would produce the same fluctuations in a noise-free receiver output as are actually observed.

The early experiments had system temperatures of several thousand degrees and receiver bandwidths of tens of MHz, which permitted. measurements to 1/10 degree in an integration time of about 1 minute. Inadequate receiver sensitivity has never been a real limit in these measurements except in the process of measuring some of the systematic noise sources, in particular the contribution from antenna side lobes, and in some of the experiments, the atmospheric radiation. The reasons for this will become clearer when each of these terms is discussed below.

The system output signal is proportional to the integral of the input power spectral density over the receiver bandwidth. The receivers, however, amplify the currents and voltages at the input terminals which are proportional to the incident electric and magnetic fields and are therefore sensitive to the phases of these fields. The receiver and antenna together are generally designed to accept one spatial mode (and often one polarization state) of the radiation field. For coherent systems like this the area - solid angle product (étendue) is ². The total power accepted from an isotropic blackbody distribution is then

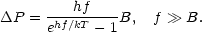(2)

The receiver systems are usually calibrated with blackbody sources for which hf /kT << 1 (Rayleigh-Jeans sources). For example at = 1 cm, T = 300 K, hf / kT ~ 5 × 10^-3 so that the receiver power is just equal to P = KTB. It becomes convenient to measure power in terms of a temperature. Measurements of the background radiation and liquid helium reference sources at wavelengths shorter than 3 cm show substantial deviations free the Rayleigh-Jeans spectrum; the power is not proportional to the thermodynamic temperature. To relate the received power to the calibration, it is useful to define the concept of an antenna temperature, T_ant. The temperature of a Rayleigh-Jeans source that radiates the same power as the actual source at a thermodynamic temperature T and frequency f:

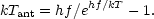(3)

The general practice has been to measure all terms in units of antenna temperature and then to convert the C BR contribution to a thermodynamic temperature. Several of the references have not been consistent in this regard and the results in Table 1 have been adjusted accordingly.