Annu. Rev. Astron. Astrophys. 1980. 18: 489-535 Copyright © 1980 by Annual Reviews. All rights reserved

(e) Galactic Background Contribution

The next "atmosphere" is the solar system and the galaxy, the "molecules" being the astrophysical phenomena distinguished by their spectra and identified by their anisotropic distribution. The individual "molecules" are not indistinguishable and can only be characterized in a statistical sense. As a consequence, the success in modeling the "local" astrophysical background depends heavily on sampling much of the sky with extended spectral coverage.

Figure 3 shows the present best estimates of known astrophysical sources that emit in the frequency range important to CBR measurements. The CBR lies predominantly in a clear region of the local astrophysical spectrum embraced by synchrotron emission of cosmic ray electrons moving in galactic magnetic fields and free-free thermal emission by ionized gas surrounding hot stars (H II regions) at low frequencies and by the thermal emission of interstellar dust at high frequencies.

Figure 3. The astrophysical background.

Full sky maps of synchrotron emission have been made at low frequencies, 200 MHz (Droge & Priester 1956) and 404 MHz (Pauliny-Toth & Shakeshaft 1962), where it is the major source of the galactic background and pervades the sky. There is no region of the sky which emits less than ~ 5% of the strongest sources contained in the galactic plane in a band b ± 10°, l ± 40°. The spectral index n, defined by I() ^-n, ranges between 0.8 to 0.9 (Witebsky 1975) as determined by high frequency measurements in selected regions of the sky. The spectral index depends on the energy distribution of the radiating electrons and may well be different in discrete sources such as supernova remnants and in the general galactic background. In clearer regions, toward the galactic poles, the antenna temperature due to synchrotron emission is approximated by

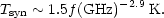Strong H II regions lie primarily in the galactic plane although the Orion nebula is a notable exception. A compilation of emission by H II regions at 5 GHz is given by Lang (1978), from data of Reifenstein et al. (1970) and Wilson et al. (1970). A proper estimate of the contribution from discrete H II source emission requires knowledge of the specific H II regions in the observing beam. Typical parameters for the stronger H II regions are electron temperatures ~ 7000 K, emission measure, N_e² d, ~ 10⁶ electron² × parsec per cm⁶, and angular size, _S, ~ 0.1°. In the spectral region of interest to CBR measurements, 1 GHz < f < 1000 GHz, quantum effects are negligible, and the optical depth in the source is much less than unity. The spectrum is almost flat, modified only by the classical Gaunt factor, giving a spectral index of approximately 0.1. The antenna temperature of such a typical H II region, when diluted in a beam of angular size _B ~ 10°, is given by (Lang 1978)

(9)

In addition to the discrete H II regions, Hirabayashi (1974) has observed a diffuse galactic background ascribed to free-free emission with an emission measure of 4000 pc cm^-6 and an average electron temperature of 3000 K, directly in the galactic plane. Combining this observation with the model proposed by Ellis & Hamilton (1966), which assumes the ionized hydrogen is distributed uniformly (N_e ~ 0.2 cm^-3) in a disk 300 pc thick on either side of the plane, gives the following estimated antenna temperature (Smoot 1977) using Equation (9):

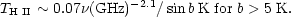The estimates for thermal emission by interstellar dust gains shown in Figure 3 are merely suggestive since both the physical properties of the dust grains as well as the dust distribution throughout the Galaxy are still poorly known. Direct measurements of interstellar dust emission in the far infrared, < 50 cm^-1, have been made solely in regions of strong emission such as in surveys of the galactic plane - at 50 cm^-1 (Low et al. 1977), at 20 and 10 cm^-1 (Owens et al. 1979) - and observations toward the galactic center at 28 cm^-1 (Gezari et al. 1973 and Rieke et al. 1973), and at 18 cm^-1 (Hildebrand et al. 1978). It has proved difficult to determine the spectrum by comparing measurements of the same objects made by instruments using different beam widths and spatial chopping techniques because many of the dusty regions are complex with both compact and diffuse emitting regions.

For 50 cm^-1, the radiating efficiency of the gains is small since the wavelength is much larger than the gain dimensions, assumed 10^-5 cm and smaller, so that even for the densest regions of the Galaxy the optical depth at < 50 cm^-1 is less than 1. The emittance of a dust column is then

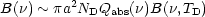(10)

where a² is a typical cross sectional area of the gain, N_B, the column density of grains, B(, T_D) the blackbody emittance at the dust temperature T_D, and Q_abs() the emissivity per grain.

The most general form of the emissivity per gain is

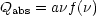(11)

where f () is a function of the imaginary part of the gain dielectric constant. The observations in strongly emitting regions indicate that f () varies as ^0.5 to ² and implies that the far infrared emission is most likely due to the low frequency tails of solid state absorption bands in the grains (Aannestad 1975).

Combining Equations 10 and 11, the dust brightness is proportional to the volume of dust and therefore to the mass column density. The dust brightness alone, however, cannot give the gain emissivities because the mass column density is not known directly. In lieu of a dust model, estimates of the dust mass column densities are made from the observed correlation of dust with neutral gas. The dust column densities, estimated by optical extinction and reddening, related to H I column densities determined from 21 cm line profiles (see for example Knapp & Kerr 1974) indicate that the dust-to-hydrogen mass ratio is of the order of 1%.

In the past few years observation of CO emission in dusty regions, where it is a minor constituent, have provided estimates of the H₂ densities, the major constituent. These measurements main give dust-to-neutral-gas ratios of ~ 1% (Scoville & Solomon 1975) and furthermore yield independent measurements of the dust temperature.

Along the galactic plane |l | < 50°, plausible parameters that fit the measured emission are T_D ~ 25 K, dust mass column density 3 × 10^-4 gm / cm², corresponding to 2 × 10²² gas atoms / cm², individual grain emissivity 2 × 10^-7( cm^-1)², a = 10^-5 cm, and a grain density of 2 gm / cm³. These are the parameters used in estimating the emission at b = 0 in Figure 3 in a beam width of 16°, the galactic plane filling about 1/15 of the beam. ⁽²⁾

The estimates of dust emission out of the plane, especially toward the galactic poles, are even more uncertain. The steps involved in the estimate are the following: the dust type is assumed to be the same out of the plane as in the plane, the temperature of the dust is calculated on the basis of radiative equilibrium with the absorption of star light T_D ~ 10 K, the dust mass column density is estimated from H I column densities, and extinction and reddening data (Heiles & Jenkins 1976, Daltabuit & Meyer 1972). Various methods of calculating the dust mass density toward the galactic poles do not agree. Reddening data of Feltz (1972) gives an extinction due to dust of 0.000 ± 0.006 map while Appenzeller (1975) infers an extinction 0.03 from stellar polarization due to dust grain alignment. The assumed ratio of gas density to visual extinction is 1.6 × 10²¹ atoms / cm² / mag or ~ 2.5 × 10^-5 gm dust / cm² / mag so that the dust column density to the galactic poles from extinction data is close to zero or larger than 7.5 × 10^-7 gm / cm²(4 × 10¹⁹ atoms / cm²), while H column densities are measured directly as 1 - 2 × 10²⁰ atoms / cm². The dust mass column density adopted for Figure 3 is 8 × 10^-7 gm / cm², at b = 90°, and to the same precision as any of these estimates, may follow a cosecant law with galactic latitude.

² The dust model isn't totally crazy; using sample Lorentz-Lorenz theory with one resonance, the emissivity per grain is (2/3)( / m_rma)(ar_e)(² / ₀⁴) where m_a is the mass per atom, assuming each atom contributes one oscillator, r_e the Thomson radius of the electron, and ₀ the resonance frequency in cm^-1 with width . Assuming ~ 1/10 ₀, ₀ ~ 1000 cm^-1, typical of silicates and carbonates, the emissivity/grain is of the same order of magnitude as used above. Back.