


3.2. Analytic modeling
Analytic `toy' models are another useful way to model the principal features of mechanical heating by AGNs. We consider the pdV work done by a spherically symmetric ensemble of bubbles rising subsonically through the pressure gradient. Since the timescale for the bubbles to cross the cluster (of order the free-fall time) is much shorter than the cooling timescale, the flux of bubble energy through the ICM approaches a steady state, implying that details of the energy injection process - such as the number flux of bubbles (e.g., one big one or many small ones), the bubble size, filling factor, and rate of rise - do not affect the mean heating rate. If we assume that the pdV work is dissipated within a pressure scale height of where it is generated, we can devise an average volume heating rate for the ICM, as a function of radius (Begelman 2001):
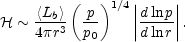 |
(3) |
In eq. (3.1), <Lb> is the time-averaged power
output of the AGN going into bubbles, p(r) is the
pressure inside the bubbles (and p0 is the pressure
where the bubbles are formed), and the exponent 1/4 equals
( - 1) /
- 1) /
 for a
relativistic plasma (the exponent would be 2/5 for a nonrelativistic
gas). A major assumption of the model, that the pdV work is
absorbed and converted to heat within a pressure scale height, will have
to be assessed using numerical simulations and studies of the
microphysics of cluster gas. We have also assumed that the energy is
spread evenly over 4
for a
relativistic plasma (the exponent would be 2/5 for a nonrelativistic
gas). A major assumption of the model, that the pdV work is
absorbed and converted to heat within a pressure scale height, will have
to be assessed using numerical simulations and studies of the
microphysics of cluster gas. We have also assumed that the energy is
spread evenly over 4 sr, a
likely consequence of buoyancy.
sr, a
likely consequence of buoyancy.
The most important property of the above effervescent heating rate is its proportionality to the pressure gradient (among other factors), since this determines the rate at which pdV work is done as the bubbles rise. Since thermal gas that suffers excess cooling will develop a slightly higher pressure gradient, the effervescent heating mechanism targets exactly those regions where cooling is strongest. Therefore, it has the potential to stabilize radiative cooling (Begelman 2001). This potential is borne out in 1D, time-dependent numerical simulations of a cooling core (Ruszkowski & Begelman 2002), which show that the flow settles down to a steady state that resembles observed clusters, for reasonable parameters and without fine-tuning the initial or boundary conditions. Although these models include conduction (at 23% of the Spitzer rate), which may be necessary for global stability (Kim & Narayan 2003), the heating is overwhelmingly dominated by the AGN at all radii. The mass inflow rate through the inner boundary, which determines the AGN feedback in these simulations, stabilizes to a reasonable value far below that predicted by cooling flow models.
According to the analytic models, a large fraction of the injected
energy reaches radii much larger than the cooling radius.
Roychowdhury et
al. (2004)
have used these models to study whether AGN heating can explain the
excess entropy of cluster gas. We find that the distributed heating rate
given by eq. (3.1) can reproduce simultaneously the
luminosity-temperature correlations measured at two different radii
(roughly 0.5 and 0.08 of the virial radius), for cluster temperatures
between 1 and 10 keV. These results appear to require a high efficiency
of kinetic energy production
( KE)
during the growth of the black hole as well as a black hole mass (or sum
of black hole masses) roughly proportional to the virial mass of the
cluster. If we assume
MBH
KE)
during the growth of the black hole as well as a black hole mass (or sum
of black hole masses) roughly proportional to the virial mass of the
cluster. If we assume
MBH  0.0015Mbulge for each galactic bulge in the cluster
(Häring & Rix
2004),
and further assume that bulges comprise a fraction
0.01f-2 of the cluster's virial mass, then the entropy
measurements require
0.0015Mbulge for each galactic bulge in the cluster
(Häring & Rix
2004),
and further assume that bulges comprise a fraction
0.01f-2 of the cluster's virial mass, then the entropy
measurements require
 KE
f-2
KE
f-2
 0.05. Realistically
this represents an upper limit,
since it was calculated assuming that all of the heating occurs at low
redshift, i.e., after each cluster has fully formed. Since most black
hole growth appears to have occurred by accretion during the `quasar
era' at z ~ 2 - 4
(Yu & Tremaine
2002),
the entropy we see today was probably injected into the lower-mass
precursors of modern clusters, which had lower virial
temperatures. According to the second law of thermodynamics, the heat
input required to produce a given change in entropy is proportional to
temperature; therefore, the required value of
0.05. Realistically
this represents an upper limit,
since it was calculated assuming that all of the heating occurs at low
redshift, i.e., after each cluster has fully formed. Since most black
hole growth appears to have occurred by accretion during the `quasar
era' at z ~ 2 - 4
(Yu & Tremaine
2002),
the entropy we see today was probably injected into the lower-mass
precursors of modern clusters, which had lower virial
temperatures. According to the second law of thermodynamics, the heat
input required to produce a given change in entropy is proportional to
temperature; therefore, the required value of
 KE
f-2 is probably smaller than the one stated above.
KE
f-2 is probably smaller than the one stated above.