Annu. Rev. Astron. Astrophys. 1982. 20: 399-429 Copyright © 1982 by Annual Reviews. All rights reserved

3. RADIAL STRUCTURE OF SPHEROIDAL COMPONENTS

The variation of mass density, luminosity density, and velocity dispersion as a function of radius are most easily discussed in terms of spherical models. These are much easier to construct than nonspherical models, and neither observation nor theory indicate that the radial profiles of nonspherical galaxies are affected in important ways by the shapes of the systems. In particular, the works of Saaf (1968) and Richstone (1981) indicate that the total angular momentum of a star is approximately conserved when it orbits in a mildly nonspherical potential.

3.1. Model Galaxies

If a galaxy is spherical, stars orbiting in its potential are constrained by four independent isolating integrals - the three components of the angular momentum vector J and the energy - and we may invoke Jeans' theorem to construct models by taking f to be an arbitrary positive function of these four integrals. If the galaxy is not only spherical, but also spherically symmetric in all its properties, f can depend on J_x, J_y and J_z only through the combination J² = J_x² + J_y² + J_z² so f is then of the form f = f (E, J).

SYSTEMS HAVING f (E)     For many years elliptical galaxies have been discussed in terms of models whose distribution functions depend only on E. These models are interesting, but it is important to recognize that they constitute a narrowly restricted class of possible, spherically symmetric galaxies, and it is unlikely that Nature confines herself to models of this type. The majority of these models are modifications of the isothermal sphere, whose distribution function is simply

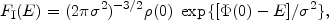(9)

where (0) is the potential energy at the center of the system. Integrating f_I over all velocities yields the density at radius r as

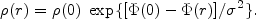(10)

If the system is self-gravitating, one obtains on solving Poisson's equation with replaced by (10),

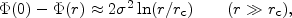(11)

where

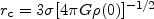(12)

is the "core radius" at which the projected density falls to very nearly 1/2 of its value at the center. Substituting Equation (11) into (10), one sees that at large radii, ~ r^-2. If the system is not self-gravitating, but sits in the potential of another isothermal population whose velocity dispersion _h differs from that of the first system, one has from equations (10) and (11) that at large radii the density of the first population falls off as ~ r^{-2(_h / )2}. Gunn (1977) has argued that the brightness profiles of galaxies may fall off more steeply than as r^-2 because the velocity dispersion of the luminous stars is less than that (_h) of the mass-bearing halo population by a factor of order / _h = 0.82.

An alternative strategy for obtaining from f_I a system that looks like an elliptical galaxy is to truncate f_I at some maximum energy E_t. Woolley (1954) simply set f equal to f_I for E less than E_t, and to zero otherwise. King (1966), in parallel with Michie (1963), eliminated the discontinuity in Woolley's distribution function at E_t, by defining for E < E_t.

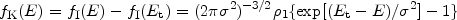(13)

Wilson (1975) subsequently eliminated the discontinuity in the gradient of f_K at E_t by defining for E < E_t,

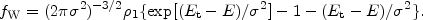(14)

Proceeding in this way one may generate a sequence of models, all of which are effectively isothermal near their centers, where E << E_t but which have nonisothermal envelopes.

Hunter (1977) has shown that the structure of the envelopes of these models depends sensitively and in a paradoxical way on the detailed form of the distribution function near the tidal cutoff. In particular, Wilson spheres, which have more heavily truncated distribution functions than King models, have much more extensive envelopes. It follows from this state of affairs that one cannot say a priori whether tidal encounters between galaxies lead to tidal truncation of the galaxies or to distension of their envelopes. The observations discussed below suggest the latter (Kormendy 1977; but see Strom & Strom 1978d).

As is discussed in Section 3.2, the brightness profiles at the centers of elliptical galaxies tend to be more peaky than the projected density of an isothermal sphere. Therefore it is interesting to study model galaxies whose projected density profiles have a cusp at the center. Eddington (1916) showed how to find the f(E) that generates a galaxy of any given radial density profile, and one may apply this apparatus (Binney 1982a) to find the distribution function f_1/4(E) that generates the galaxy whose projected surface density obeys de Vaucouleurs' (1948) r^1/4 law of surface brightness. One finds that f_1/4(E) rises steeply at energies that correspond to stars confined to the center of the galaxy. It is this abundance of tightly bound stars that gives rise to the central density peak and velocity dispersion depression (Bailey & MacDonald 1981) that are characteristic of the r^1/4 model. Binney (1982a) has proposed a theoretical interpretation of this model.

SYSTEMS HAVING f(E, J)     Eddington (1914; see also Shiveshwarkar 1936) considered simple models, based on f = f(E, J), that can probably not be used to describe any real system, but which do illustrate the way in which velocity dispersion anisotropy affects the structure of spherical systems. The distribution functions of these Eddington models are of the form

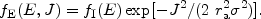(15)

The part of Eddington's distribution function (15) that depends on J causes the density at radius r to drop from the value [Equation (10)] associated with the isothermal sphere to

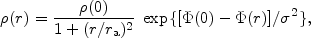(16)

and causes each tangential component of squared velocity dispersion to diminish by a fraction of the radial component of , where

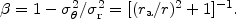(17)

Thus the velocity dispersion tensor in an Eddington model is isotropic at the center and wholly anisotropic at large radii. The radial component of velocity dispersion equals the constant at all radii.

The outermost part of most Eddington models is an envelope in which ~ r^-2 . This envelope bears a superficial resemblance to the outermost portion of the isothermal sphere, but it is actually of an entirely different nature because the circular velocity v_c(r) in an Eddington model tends to zero as r increases, rather than to a finite constant as in the isothermal sphere (v_c = 2^1/2 ) . On the other hand, the radial component of velocity dispersion in an Eddington model is always equal to . Therefore the gravitational attraction of stars interior to r slows or deflects the motion of a star with typical speed less and less as r increases, and stars far from the core of an Eddington model execute giant oscillations in radius. The system becomes, in fact, a kind of stellar traffic jam in which each star moves with more or less uniform velocity on a radial path. The ~ r^-2 increase of density toward the center has less to do with gravity and dynamics than with congestion of these trajectories. In terms of Equation (7), one may say that at the outside of an Eddington model the term on the right-hand side of this equation has dropped out, leaving the structure to be determined by a balance between the two terms on the left.

Color gradients (de Vaucouleurs 1961, Strom & Strom 1978a, b, c) in principle offer a way of constraining the degree of radial velocity anisotropy in a galaxy. If all the stars of a galaxy were on circular orbits, so that the galaxy could be considered to be constructed of infinitesimally thin spherical shells, color changes could be perfectly sharp in three-dimensional space and moderately sharp when projected onto the sky. If, on the other hand, the system resembled the asymptotic portion of an Eddington model, all stars would contribute equally to the light at each radius, and no color gradient would be possible.

Michie (1963) studied the models that are related to King models in the same way that Eddington models are related to the isothermal sphere. The distribution function of a Michie model is

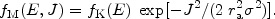(18)

For sufficiently large anisotropy radius r_a, a Michie model behaves like a King model in that it has a "tidal radius" at which the density goes to zero. When r_a is small, the Michie model has an infinite envelope that resembles the envelope of an Eddington model. The Michie models that are of the. greatest interest from the point of view of modeling real galaxies are those that have finite tidal radii. In these models the anisotropy parameter never comes close to unity.