Copyright © 1982 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1982. 20:
399-429 Copyright © 1982 by Annual Reviews. All rights reserved |
3.2. Observations of Radial Structure
PHOTOMETRY Unfortunately, many spectroscopic data cannot yet be interpreted dynamically because the requisite photometry is lacking. Furthermore, the interpretation of the available photometry is more controversial than is the interpretation of the spectroscopic observations.
It is convenient to divide the brightness profile of a typical
elliptical galaxy into an inner part that extends out to
RI =
5 s ,
where
s ,
where  s ~
0.75" is the
dispersion of the central Gaussian component of a typical seeing disk, an
intermediate part that runs from this radius out to the de Vaucouleurs
radius RD (the radius where the B brightness falls to
µ = 25 mag / arcsec2), and the
part that lies outside RD. The true brightness
distributions of spheroidal systems in their inner and outer parts are
very difficult to measure and are
correspondingly uncertain. The profiles in the intermediate region are, by
contrast, fairly well determined.
s ~
0.75" is the
dispersion of the central Gaussian component of a typical seeing disk, an
intermediate part that runs from this radius out to the de Vaucouleurs
radius RD (the radius where the B brightness falls to
µ = 25 mag / arcsec2), and the
part that lies outside RD. The true brightness
distributions of spheroidal systems in their inner and outer parts are
very difficult to measure and are
correspondingly uncertain. The profiles in the intermediate region are, by
contrast, fairly well determined.
The radial brightness profiles of a sample of 17 elliptical galaxies
studied by
King (1978)
are very similar to one another in the intermediate region,
though the profiles do show some genuine individuality (see Figure 1 of
Kormendy 1977).
The ellipticity of King's galaxies, which varies from
 = 0
to
= 0
to  = 0.4 appears not
to affect the mean radial brightness profile.
= 0.4 appears not
to affect the mean radial brightness profile.
A variety of fitting functions provide satisfactory fits to the profiles of King's galaxies in the intermediate range of radii, although Kormendy (1977) concludes that the r1/4 law provides a more convenient overall fit than the Hubble-Reynolds or King profiles. A particularly striking, example of the quality of fit to observations of elliptical galaxies that can be obtained with the r1/4 law is provided by, the. extensive study by de Vaucouleurs & Capaccioli (1979) of the surface brightness of the E1 galaxy NGC 3379. They show that the r1/4 law of surface brightness fits the observations of this galaxy to within 0.1 mag over a range of 9 mag in surface brightness.
The brightness profiles of galaxies below about 26 mag / arcsec2 are rather problematical. The B-band sky brightness in these outer regions typically exceeds the galaxian surface brightness by a factor of more than 100, so that a small error in the choice of sky brightness level to be subtracted from the raw observations can lead to a large error in the derived galaxian brightness profile. Published photometry indicates that the behavior of brightness profiles beyond RD is highly variable. Kormendy (1977) finds that the surface brightnesses of King's ellipticals always exceed that of the best-fitting r1/4 law at large radii, and they sometimes exceed that of the best-fitting Hubble profile. The latter phenomenon occurs most commonly amongst galaxies that have companions, as if elliptical galaxies are distended rather than truncated by tidal encounters.
In a log-log plot, the brightness profiles of all of King's galaxies steepen fairly steadily with increasing radius. By contrast, certain supergiant galaxies studied by Oemler (1976), Dressler (1978), Carter (1978), Hoessel et al. (1980) and others have brightness, profiles whose slopes in a log-log plot flatten at large radii. The designation cD, which is sometimes used rather loosely, is best confined to galaxies of this class.
The bulges of disk galaxies show a general similarity to elliptical galaxies (e.g. Kormendy 1977, Tsikoudi 1980) although there are differences in detail. Unambiguous information about bulges can only be obtained from the minor-axis profiles of edge-on galaxies, for only profiles of this type are uncontaminated by an uncertain contribution from the disk. The bulge of the edge-on Sb galaxy NGC 4565, which has been studied by Hegyi & Gerber (1977), Spinrad et al. (1978), and Kormendy & Bruzual (1978) cannot be fitted over the range 21 < µv < 28 by either a single Hubble law or a simple r1/4 law. It is not known whether this phenomenon is widespread among the bulges of disk galaxies, although Burstein (1979) finds that the profiles of edge-on SO galaxies also cannot be exactly fitted by the r1/4 law.
It has been suggested (Freeman; report to NATO ASI, Cambridge 1980) that these differences may be due to distortion of the bulges by the gravitational field of the disk. It is also possible that all low-luminosity spheroidal components, including dwarf ellipticals, have profiles that differ systematically from those; of giant ellipticals (Strom & Strom 1979).
The true shapes of the brightness profiles of spheroidal systems at radii
comparable to the core of the point-spread function (PSF) imposed by seeing
are highly controversial.
Schweizer (1979,
1981)
has recently studied the
results of convolving ideal galaxy profiles with various model PSFs in some
detail. His conclusions are as follows: (a) A seeing-convolved
r1/4 profile looks
much like an unconvolved King profile. The apparent core radius of this
profile is typically 3-4 times the dispersion
 s of the
Gaussian core of the PSF.
(b) A seeing-convolved King profile looks like an unconvolved King
profile of larger core radius. The ratio
rc, app / rc of the
apparent to the true core radius does not fall to 1.25 until
rc, app >
3.5
s of the
Gaussian core of the PSF.
(b) A seeing-convolved King profile looks like an unconvolved King
profile of larger core radius. The ratio
rc, app / rc of the
apparent to the true core radius does not fall to 1.25 until
rc, app >
3.5 s.
(c) The predicted profiles are changed
materially by the inclusion in the PSF of exponential wings or additional
Gaussian components, such as those advocated by
Brown (1974)
and by
de Vaucouleurs & Nieto
(1979).
s.
(c) The predicted profiles are changed
materially by the inclusion in the PSF of exponential wings or additional
Gaussian components, such as those advocated by
Brown (1974)
and by
de Vaucouleurs & Nieto
(1979).
When one reviews the apparent core radii of the galaxies studied by King in the light of these results, one finds that the photometric data are in most cases unable to distinguish between the possibility that these galaxies have regions of constant density at their centers similar to that of a King model, or have volume densities of stars that rise towards a singularity of the type required to generate the r1/4 law in projection. However, external evidence suggests that these galaxies are likely to have rather singular central densities: Schweizer (1979) notes that the spheroidal components of the Local Group galaxies M31 and M32 have central surface brightnesses that are 2-3 mag brighter than those inferred by fitting King models to King's sample of giant ellipticals. They are, however, very 'much in the range of central surface brightnesses inferred from King's sample by fitting r1/4 profiles. This suggests that giant elliptical galaxies appear less centrally concentrated than M31 and M32 only because they are more distant and therefore less well resolved. Furthermore, neither counts of RR Lyrae stars and globular clusters toward the center of our Galaxy (Oort 1976) nor studies of the gas at the Galactic center (Lacy et al. 1979) provide any evidence that our Galaxy has a quasi-isothermal core.
Two spheroidal components whose central regions have been carefully studied are M87 and the bulge-nucleus of M31. Young et al. (1978b) obtained high signal-to-noise V-band observations of the central 80" of M87. They found that the brightness distribution near the center of M87 cannot be fitted with a King model or a King model plus a point light source. De Vaucouleurs & Nieto (1979) have confirmed the photometry of Young et al. and concluded that M87 has less light in the radius range r < 8" than the r1/4 law fitted to the observations beyond r = 8" would require. The ground-based observations of M31 by Johnson (1961), together with data collected by the balloon-borne telescope Stratoscope II, show (Light et al. 1974) that interior to r = 20" the brightness profile of M31. is qualitatively similar to that of M87. Again there is a clearly defined shoulder in the brightness distribution somewhat outside the region where seeing markedly degrades ground-based observations. Interior to this shoulder the surface brightness first flattens off and then rises again steeply to a peak surface brightness that is determined by the PSF of the observations. The brightness profiles of M87 and M31 are associated with the velocity dispersion anomalies discussed below.
SPECTROSCOPY Great strides have been made over the last six years in the absorption-line spectroscopy of early-type systems. Until a few years ago, very few systems had been observed spectroscopically even near their centers, where they are brightest. Furthermore, the few measurements that were available showed a distressingly wide spread of values for the same system when measured by different observers. The introduction of automatic algorithms for the reduction of spectra has transformed this situation.
Two quite independent methods of obtaining kinematic information from absorption-line spectra are now in use. The majority of workers use some variant of the Fourier quotient technique that was originally developed by Illingworth (1976) and Schechter (Sargent et al. 1977). Data collected in the extensive Harvard survey of galactic velocities in the Local supercluster (Tonry & Davis 1981a, b) have been analyzed with a cross-correlation algorithm (Tonry & Davis 1979). Efstathiou et al. (1980) have found that these two methods yield very similar results when applied to the same data. Terlevich et al. (1981) find that velocity dispersions obtained for one galaxy by different observers using different equipment and reduction techniques now agree to within the ~ 10% cited errors. Differential velocities within galaxies are commonly measured to an accuracy of 20 km s-1 or better.
Two types of data must be considered. The ideal study yields the velocity dispersion and mean velocity as a function of position in the galaxy from the center far out into the halo. Studies that approach this ideal have now been carried out on a few dozen galaxies of type E and SO (Sargent et al. 1977, 1978, Young et al. 1978a, Schechter & Gunn 1979, Efstathiou et al. 1980, Davies 1981, Carter et al. 1981, Illingworth & Schechter 1981, Kormendy & Illingworth 1982, Kormendy 1981a, b, Fried & Illingworth, in preparation, Davies et al., in preparation). A much less time-consuming observation involves measuring the systematic velocity and the velocity dispersion from a single spectrum of the light from the center of the galaxy. Measurements of this type have now been obtained for a few hundred galaxies of type E and S0 (Faber & Jackson 1976, Schechter 1980, Tonry & Davis 1981a, b, Faber et al., in preparation).
These data show that the central line-of-sight velocity dispersion
 v0 is
tightly correlated with total luminosity L.
Faber & Jackson (1976)
found the velocity dispersion of a sample of 24 E and S0 galaxies to be well
represented by the law L ~
v0 is
tightly correlated with total luminosity L.
Faber & Jackson (1976)
found the velocity dispersion of a sample of 24 E and S0 galaxies to be well
represented by the law L ~
 v04 .
Several subsequent investigations
(Sargent et al. 1977,
Schechter & Gunn
1979,
Schechter 1980,
Terlevich et al. 1981,
Tonry & Davis 1981b)
have confirmed that
v04 .
Several subsequent investigations
(Sargent et al. 1977,
Schechter & Gunn
1979,
Schechter 1980,
Terlevich et al. 1981,
Tonry & Davis 1981b)
have confirmed that
 v0 and
L are well correlated, although the
value of the slope n when the correlation is fitted to the power
law L ~
v0 and
L are well correlated, although the
value of the slope n when the correlation is fitted to the power
law L ~
 v0n
has varied in the range 3 < n < 5. Probably the correlation
cannot be adequately
fitted by a single power law over the full range of absolute magnitudes
(-23 < M < -15.5) for which corresponding velocity
dispersions are now available.
Tonry (1981)
finds that at faint luminosities,
v0n
has varied in the range 3 < n < 5. Probably the correlation
cannot be adequately
fitted by a single power law over the full range of absolute magnitudes
(-23 < M < -15.5) for which corresponding velocity
dispersions are now available.
Tonry (1981)
finds that at faint luminosities,
 v0 rises more
steeply than L1/4 , and
Efstathiou et
al. (1980) and
Malmuth & Kirshner
(1981)
find that luminous cD galaxies have smaller velocity dispersions than the
extrapolation of
v0 rises more
steeply than L1/4 , and
Efstathiou et
al. (1980) and
Malmuth & Kirshner
(1981)
find that luminous cD galaxies have smaller velocity dispersions than the
extrapolation of
 v0 ~
L1/4 would suggest.
v0 ~
L1/4 would suggest.
The more luminous an elliptical galaxy is, the more strongly lined is the
light it emits (e.g.
Faber 1973).
A useful measure of line strength is the Mg2,
index defined by
Faber et al. (1977).
Terlevich et al. (1981)
have investigated
the distribution of the representative points of galaxies in the
three-dimensional space defined by L,
 v0 and
Mg2. They argue that in this space all
but 4 of a sample of 24 galaxies lie in a long flat volume like that
occupied by a ruler; that is, Terlevich et al. conclude that elliptical
galaxies form a two-parameter family.
Tonry & Davis (1981b)
have discussed the distribution of a sample of more than 50 ellipticals
in a similar three-dimensional space.
They conclude that the galaxies are distributed in this space within a long
cylinder that has three full dimensions, and they go on to argue that the
analysis of Terlevich et al. suggested that part of that sample occupies a
two-dimensional space only because the analysis failed to eliminate the
elongation of the cylinder occupied by the sample. Terlevich et
al. reply that the errors in the data of Tonry & Davis are too large
for two-dimensionality to be
detectable. Work is now in progress on observations that should resolve
this controversy. If the main finding of Terlevich et al. is confirmed,
it will be interesting to see whether the second parameter among
elliptical galaxies is, as Terlevich et al. suggest, true ellipticity.
v0 and
Mg2. They argue that in this space all
but 4 of a sample of 24 galaxies lie in a long flat volume like that
occupied by a ruler; that is, Terlevich et al. conclude that elliptical
galaxies form a two-parameter family.
Tonry & Davis (1981b)
have discussed the distribution of a sample of more than 50 ellipticals
in a similar three-dimensional space.
They conclude that the galaxies are distributed in this space within a long
cylinder that has three full dimensions, and they go on to argue that the
analysis of Terlevich et al. suggested that part of that sample occupies a
two-dimensional space only because the analysis failed to eliminate the
elongation of the cylinder occupied by the sample. Terlevich et
al. reply that the errors in the data of Tonry & Davis are too large
for two-dimensionality to be
detectable. Work is now in progress on observations that should resolve
this controversy. If the main finding of Terlevich et al. is confirmed,
it will be interesting to see whether the second parameter among
elliptical galaxies is, as Terlevich et al. suggest, true ellipticity.
Whitmore et al. (1979)
have measured the central velocity dispersions of 21
spiral galaxies and plotted their results against estimates of the
absolute bulge magnitudes of these systems, which span the range
-17.5 > MB > -22.7.
Their results are consistent with L ~
 v04
over this range, although the dispersion at a given L may be 15% lower
than in an equivalent elliptical.
However, the bulges of spirals cannot be self-gravitating at all radii
because observations of neutral hydrogen in the disks surrounding them
show that the circular velocity
vc
v04
over this range, although the dispersion at a given L may be 15% lower
than in an equivalent elliptical.
However, the bulges of spirals cannot be self-gravitating at all radii
because observations of neutral hydrogen in the disks surrounding them
show that the circular velocity
vc  31/2
31/2
 v0 at large radii
(Whitmore et al. 1979).
If the bulges were everywhere self-gravitating, one would have
vc < 21/2
v0 at large radii
(Whitmore et al. 1979).
If the bulges were everywhere self-gravitating, one would have
vc < 21/2
 v0 far
from the center. Nonetheless the bulges probably are self-gravitating at
their centers.
v0 far
from the center. Nonetheless the bulges probably are self-gravitating at
their centers.
It is remarkable that
 v0 should be
tightly correlated with L, for
v0 should be
tightly correlated with L, for
 v0 depends
on the structure of the galaxy in a small region that contributes very
little of the total light. Furthermore, the velocity dispersion in most
elliptical galaxies declines from the nucleus outward (see Figure 3 of
Illingworth 1981),
so that the velocity dispersion that is so well correlated with luminosity
is not the velocity dispersion of the stars that contribute most of the
light. Possible
explanations of how
v0 depends
on the structure of the galaxy in a small region that contributes very
little of the total light. Furthermore, the velocity dispersion in most
elliptical galaxies declines from the nucleus outward (see Figure 3 of
Illingworth 1981),
so that the velocity dispersion that is so well correlated with luminosity
is not the velocity dispersion of the stars that contribute most of the
light. Possible
explanations of how  and
L can be correlated have been offered
by Sargent et al. (1977)
and by Tonry (1981),
but before assessing the plausibility of these
pictures it is necessary to clarify one's ideas concerning the relationship
between a galaxy's brightness and velocity dispersion profiles and its
mass-to-light ratio.
and
L can be correlated have been offered
by Sargent et al. (1977)
and by Tonry (1981),
but before assessing the plausibility of these
pictures it is necessary to clarify one's ideas concerning the relationship
between a galaxy's brightness and velocity dispersion profiles and its
mass-to-light ratio.
Suppose the velocity dispersion tensor in a spherical galaxy of known
central velocity dispersion
 is isotropic. Then two
simple methods will lead
from surface photometry of the galaxy to a fairly reliable estimate of the
mass-to-light ratio near the center of the galaxy.
is isotropic. Then two
simple methods will lead
from surface photometry of the galaxy to a fairly reliable estimate of the
mass-to-light ratio near the center of the galaxy.
1. Fit a King model to the central brightness distribution to determine the apparent core radius rc and central surface luminosity I0 of the fit. Then substitute these into the formula (King & Minkowski 1972)
 |
(19) |
The effects of seeing on results obtained with this formula are unimportant, because seeing transforms the brightness profile of a King model into a profile that closely resembles that of a King model of larger core radius but equal velocity dispersion (Schweizer 1979).
2. Fit an r1/4 profile to the photometry to determine the effective radius re and the associated surface luminosity Ie at re, and then substitute them into the formula
 |
(20) |
This formula is derived by assuming that the observed central line-of-sight
velocity dispersion is equal to the peak line-of-sight velocity
dispersion 0.469
GM / re predicted for an r1/4
model of total mass M by
Bailey & MacDonald
(1981),
and by using the standard relation L = 7.22 Ie
 re2
for the total light of
the r1/4 profile. Equation (20) is to be preferred to
the similar relationship that
relates M / L to the luminosity-weighted velocity dispersion
re2
for the total light of
the r1/4 profile. Equation (20) is to be preferred to
the similar relationship that
relates M / L to the luminosity-weighted velocity dispersion
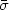 of an
r1/4 model
(Poveda et al. 1960),
because the latter is not what is usually measured. (Half
the light of the r1/4 model is received at surface
brightnesses fainter than
(Ie / 4
of an
r1/4 model
(Poveda et al. 1960),
because the latter is not what is usually measured. (Half
the light of the r1/4 model is received at surface
brightnesses fainter than
(Ie / 4  ) ~
23 mag / arcsec2.) When, as sometimes
happens,
) ~
23 mag / arcsec2.) When, as sometimes
happens,  v0
is used in Poveda's formula in place of
v0
is used in Poveda's formula in place of
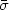 , the
mass-to-light ratio recovered is too great by a factor of 2
(Michard 1980).
, the
mass-to-light ratio recovered is too great by a factor of 2
(Michard 1980).
Schechter (1980)
has used method 1 and
Michard (1980)
has used method
2 to derive M / L for numbers of early-type galaxies. They
find 5 < (M / LB) < 12 in solar
units. The indications regarding the dependence of
M / L on L are confusing. On the one hand, two
arguments suggest that M / L should increase with L:
Tinsley (1978)
showed that M / L should increase as
L0.13 because the stars of luminous galaxies are metal
rich; and if L increases
with re less rapidly than re
(Michard 1979,
Kormendy 1977),
L can rise as
 4
only if M / L rises with L. On the other hand,
neither Schechter nor
Michard (1980)
were able to find any clear indications in the data that
M / L increases with L, notwithstanding the earlier
work of
Faber & Jackson
(1976),
who found M / L ~ L0.5 .
4
only if M / L rises with L. On the other hand,
neither Schechter nor
Michard (1980)
were able to find any clear indications in the data that
M / L increases with L, notwithstanding the earlier
work of
Faber & Jackson
(1976),
who found M / L ~ L0.5 .
Simien et al. (1979) and Whitmore et al. (1979) find similar values of M / LB for the bulges of spiral galaxies.
For many galaxies, velocity dispersions are available to large distances
from the center, and more sophisticated interpretation of the data is
called for than
is possible by merely fitting these systems with King or
r1/4 models. The most
general model of a spherically symmetric galaxy involves four functions of
radius: the luminosity density
 (r), the radial
component of the velocity dispersion tensor
(r), the radial
component of the velocity dispersion tensor
 r(r) ,
the anisotropy parameter
r(r) ,
the anisotropy parameter
 (r)
defined by Equation (8c), and the mass-to-light ratio
M / L = A(r). The luminosity density may be
determined from good photometry, and Equation (7) relates one of the
remaining unknown functions to the other two. Hence if one unknown
function is chosen a priori, for example by setting
(r)
defined by Equation (8c), and the mass-to-light ratio
M / L = A(r). The luminosity density may be
determined from good photometry, and Equation (7) relates one of the
remaining unknown functions to the other two. Hence if one unknown
function is chosen a priori, for example by setting
 = constant
or A = constant, the other may, in principle, be determined from the
observed run of velocity dispersion with radius.
= constant
or A = constant, the other may, in principle, be determined from the
observed run of velocity dispersion with radius.
Sargent et al. (1978)
chose to interpret their combined spectroscopic and
photometric observations of the inner 80" of M87 in terms of a model in which
 = 0 and
A is allowed to vary. They concluded that under these hypotheses
the mass-to-light ratio A has to increase markedly towards the
center, where
M / L ~ 60 is about a factor 10 higher than in the body of the
galaxy. They suggest that this may be due to the presence of a black
hole at the center of the galaxy.
= 0 and
A is allowed to vary. They concluded that under these hypotheses
the mass-to-light ratio A has to increase markedly towards the
center, where
M / L ~ 60 is about a factor 10 higher than in the body of the
galaxy. They suggest that this may be due to the presence of a black
hole at the center of the galaxy.
One may argue, however, that if either A or
 has to be
arbitrarily set equal
to a constant, it makes more sense to fix A and to allow
has to be
arbitrarily set equal
to a constant, it makes more sense to fix A and to allow
 to
vary, rather than
vice versa. All types of elliptical galaxies seem to have similar
overall mass-to-light ratios despite the large ranges of metallicity and
stellar density among these systems. This suggests that there is a
standard mix of stars out of which elliptical galaxies are made. And the
studies of rotation in giant elliptical
galaxies (see below) show unambiguously that the velocity dispersion
tensors in flattened galaxies are not isotropic, and their anisotropy
has nothing to do with rotation. Therefore we must examine carefully the
possibility that the velocity dispersion tensors in all elliptical
galaxies, including spherical systems, are anisotropic.
to
vary, rather than
vice versa. All types of elliptical galaxies seem to have similar
overall mass-to-light ratios despite the large ranges of metallicity and
stellar density among these systems. This suggests that there is a
standard mix of stars out of which elliptical galaxies are made. And the
studies of rotation in giant elliptical
galaxies (see below) show unambiguously that the velocity dispersion
tensors in flattened galaxies are not isotropic, and their anisotropy
has nothing to do with rotation. Therefore we must examine carefully the
possibility that the velocity dispersion tensors in all elliptical
galaxies, including spherical systems, are anisotropic.
Duncan & Wheeler
(1980)
have shown that the Sargent et al. data for M87
are fitted moderately well by a point light source plus an Eddington
model with a central mass-to-light ratio
M / Lv = 7.1. However, the model
proposed by Duncan & Wheeler has
 > 0.9 for
r > 1.7 kpc and
> 0.9 for
r > 1.7 kpc and
 > 0.99
for r > 5.5
kpc. Such highly anisotropic distributions are not very plausible.
> 0.99
for r > 5.5
kpc. Such highly anisotropic distributions are not very plausible.
This situation prompted
Binney & Mamon (1982)
to investigate the problem posed by observations of
 v(r)
and I(r) more generally. They show that if one
presumes that the mass-to-light ratio A is (an initially unknown)
constant, a given run of
v(r)
and I(r) more generally. They show that if one
presumes that the mass-to-light ratio A is (an initially unknown)
constant, a given run of
 v(r)
and I(r) determine A as an
eigenvalue associated with the system of equations from which one obtains
v(r)
and I(r) determine A as an
eigenvalue associated with the system of equations from which one obtains
 (r).
If
(r).
If  (r) is
physically plausible (in particular if
(r) is
physically plausible (in particular if
 < 1 at
all r), one has then recovered the unique
spherical model that has constant mass-to-light ratio and is compatible
with the observations. Binney & Mamon apply this technique to the
Sargent et al. observations of M87. They recover a model in which M /
Lv = 7.6,
< 1 at
all r), one has then recovered the unique
spherical model that has constant mass-to-light ratio and is compatible
with the observations. Binney & Mamon apply this technique to the
Sargent et al. observations of M87. They recover a model in which M /
Lv = 7.6,
 < 0.9
everywhere, and
< 0.9
everywhere, and
 ~ 0.4 in the
body of the galaxy.
~ 0.4 in the
body of the galaxy.
The central region of M31 poses a problem that is in many respects similar
to that posed by M87. Setting
 = 0 and
assuming constant mass-to-light ratio,
Ruiz (1976)
concluded from the photometry of
Johnson (1961) and
Light et al. (1974)
that the velocity dispersion
= 0 and
assuming constant mass-to-light ratio,
Ruiz (1976)
concluded from the photometry of
Johnson (1961) and
Light et al. (1974)
that the velocity dispersion
 n at the
center of M31 should be smaller than that
(
n at the
center of M31 should be smaller than that
( b) at
10" by a factor of about 0.6. However,
Morton et al. (1977)
and Whitmore (1980)
find that
b) at
10" by a factor of about 0.6. However,
Morton et al. (1977)
and Whitmore (1980)
find that  n
is if anything larger than
n
is if anything larger than
 b . As
Tremaine & Ostriker
(1982)
point out, these results can be understood if (a)
b . As
Tremaine & Ostriker
(1982)
point out, these results can be understood if (a)
 = 0 and the
mass-to-light ratio in the nucleus is greater than in the bulge by
a factor of about 5, or (b) if
= 0 and the
mass-to-light ratio in the nucleus is greater than in the bulge by
a factor of about 5, or (b) if
 ~ 1 and the
mass-to-light ratio in the nucleus is smaller than in the bulge.
~ 1 and the
mass-to-light ratio in the nucleus is smaller than in the bulge.
The mass-to-light ratios in spiral galaxies are known to increase from the
centers outward (e.g.
Rubin et al. 1978)
and one might anticipate a similar
increase of M / L toward the outer regions of elliptical
galaxies. Unfortunately the same uncertainty as to the behavior of the
anisotropy parameter
 that
makes interpretation of observations of M87 difficult bedevils attempts to
demonstrate observationally that elliptical galaxies have large M
/ L far from their centers. The most convincing evidence that at
least some ellipticals do show this effect is provided by
Dressler's (1979)
observations of the cD galaxy in the cluster Abell 2029 and by observations of IC 2082 by
Carter et al. (1981).
Dressler found that the velocity dispersion in his cD galaxy
rises from 380 km s-1 at the center to about 470 km
s-1 at 100 kpc. From 10-100 kpc,
the data indicate that the velocity dispersion is fairly constant at
~ 450 km s-1 ,
but Dressler notes that his measurements at 10 kpc may be affected by light
from a superposed galaxy. Dressler's surface photometry indicates that the
volume luminosity density
that
makes interpretation of observations of M87 difficult bedevils attempts to
demonstrate observationally that elliptical galaxies have large M
/ L far from their centers. The most convincing evidence that at
least some ellipticals do show this effect is provided by
Dressler's (1979)
observations of the cD galaxy in the cluster Abell 2029 and by observations of IC 2082 by
Carter et al. (1981).
Dressler found that the velocity dispersion in his cD galaxy
rises from 380 km s-1 at the center to about 470 km
s-1 at 100 kpc. From 10-100 kpc,
the data indicate that the velocity dispersion is fairly constant at
~ 450 km s-1 ,
but Dressler notes that his measurements at 10 kpc may be affected by light
from a superposed galaxy. Dressler's surface photometry indicates that the
volume luminosity density
 (r) in this galaxy
decreases as a power law
(r) in this galaxy
decreases as a power law
 ~ r-2.37
over the range 10 kpc < r < 100 kpc, with the
result that if the
velocity dispersion is assumed to be isotropic and constant over this
range, Equation (7) indicates that M / L rises as
~ r0.37 between 10 kpc and 100 kpc,
or by a factor of 2.3. In fact, Dressler's conclusion that in this
galaxy M / L
increases outward seems secure so long as the velocity dispersion tensor
there is not strongly anisotropic.
Carter et al. (1981)
find that the velocity dispersion in IC 2082 rises from 260 km
s-1 at the center to 300 km s-1 at about 23 kpc. IC 2082, which lies toward the center of a
Bautz-Morgan type I-II
cluster, has a rather complex structure involving a faint nucleus ~ 8
kpc from the main nucleus of the galaxy. In view of this substructure
and the absence of complete photometry, it is difficult to arrive at a
secure interpretation of the
measurements of Carter et al. However, the same arguments that led Dressier
to conclude that M/L increases toward the outside of the
central galaxy in Abell 2029, suggest that IC 2082 also has variable M / L.
~ r-2.37
over the range 10 kpc < r < 100 kpc, with the
result that if the
velocity dispersion is assumed to be isotropic and constant over this
range, Equation (7) indicates that M / L rises as
~ r0.37 between 10 kpc and 100 kpc,
or by a factor of 2.3. In fact, Dressler's conclusion that in this
galaxy M / L
increases outward seems secure so long as the velocity dispersion tensor
there is not strongly anisotropic.
Carter et al. (1981)
find that the velocity dispersion in IC 2082 rises from 260 km
s-1 at the center to 300 km s-1 at about 23 kpc. IC 2082, which lies toward the center of a
Bautz-Morgan type I-II
cluster, has a rather complex structure involving a faint nucleus ~ 8
kpc from the main nucleus of the galaxy. In view of this substructure
and the absence of complete photometry, it is difficult to arrive at a
secure interpretation of the
measurements of Carter et al. However, the same arguments that led Dressier
to conclude that M/L increases toward the outside of the
central galaxy in Abell 2029, suggest that IC 2082 also has variable M / L.
In normal giant elliptical galaxies the velocity dispersion is not
observed to increase at large radii (see Figure 9 of
Davies 1981).
In some galaxies, for example NGC 3379 and NGC 4472, the velocity dispersion decreases with
increasing radius as rapidly as the simplest spherical stellar models
predict. In other galaxies, notably NGC 4697, the velocity dispersion does not diminish
outward so rapidly. It is still unclear whether these variations in the
behavior of
 v with
r may be understood in terms of models that
have constant M / L.
Binney (1980b)
has shown that variations in the brightness profiles of
elliptical galaxies lead to interesting variations in the
v with
r may be understood in terms of models that
have constant M / L.
Binney (1980b)
has shown that variations in the brightness profiles of
elliptical galaxies lead to interesting variations in the
 (r)
profiles of these galaxies,
even when M / L is assumed constant and the velocity
dispersion tensor isotropic. But it is possible that observations of
some normal elliptical galaxies
may not be compatible with constant M / L at large radii.
(r)
profiles of these galaxies,
even when M / L is assumed constant and the velocity
dispersion tensor isotropic. But it is possible that observations of
some normal elliptical galaxies
may not be compatible with constant M / L at large radii.