Copyright © 1982 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1982. 20:
399-429 Copyright © 1982 by Annual Reviews. All rights reserved |
For many years it was taken for granted (e.g. Sandage 1961) that galaxies are axisymmetric oblate bodies. Recently this assumption has been questioned by a number of workers for reasons that are part observational and part theoretical (Stark 1977, Williams & Schwarzschild 1979, Binney 1978b, Miller & Smith 1980). At present, it would be unwise to rule out the possibility that all elliptical galaxies are oblate and axisymmetric, but this now seems very unlikely. In this subsection, I review the theoretical situation as regards both axisymmetric and triaxial systems. The axisymmetric models are likely to be good guides to the structure of nearly axisymmetric triaxial bodies in the same way that spherical systems help us to understand the radial structure of mildly nonspherical galaxies, and they may well have direct application as models of any truly axisymmetric spheroidal components.
AXISYMMETRIC MODELS The energy E and the component of angular momentum about the symmetry axis of the system Jz are always integrals of the motion for a star orbiting in an axisymmetric galaxy, and the simplest models of nonspherical galaxies have distribution functions that depend only on E and Jz . These models are special in that everywhere within them the velocity dispersion in the radial direction equals that parallel to the symmetry axis (i.e. <vR2> = <vz2>). This is unfortunate because in the solar neighborhood, stars that belong to the galactic halo, for example the halo RR Lyrae stars, have <vR2> ~ 4 <vz2> (Woolley 1978). However, there may be some systems, for example globular clusters, to which these models do apply, and it is useful to consider the structure of the simplest axisymmetric models before passing on to more general (and much more intractable) models.
Models from distribution functions Prendergast & Tomer (1970; henceforth referred to as PT) pioneered the study of models based on f (E, Jz) by constructing models based on distribution functions of the form
 |
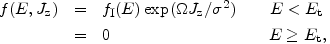(21) |
where fI is defined by Equation (9). Near the center
of these models the rotation speed
<v
> rises as
<v> =
R and is
constant on cylinders. At points that
are more than halfway to the tidal surface, the rotation speed declines
with increasing radius and, in fact, vanishes at the tidal surface
itself. In the outer
portion the rotation speed is approximately constant on spheroids.
The flattening of the isodensity surfaces in the PT models reflects the shape of the rotation curve. At the center and near the tidal surface, the isodensity surfaces tend to be round, so that the galaxy is strongly flattened only near the peak in the rotation curve. Hunter (1977) has shown that any distribution function that is the product of a function of E and a function of Jz must generate a model whose isodensity surfaces become spherical at the center.
Wilson (1975) used an improved version of the computational method introduced by PT to construct models whose distribution functions are of the form
 |
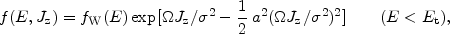(22) |
where fW is given by Equation (14) and a is an
additional parameter. When
a 
0, this
distribution function differs from that of PT only in
that its energy
dependence is that of a Wilson sphere rather than that of a Woolley
model. The general characteristics of these models are very similar to
those of the PT models. The parameter a in Equation (22) causes the
rotation. curve to flatten off at a radius that is independent of the
tidal radius. Unfortunately, when
a 0 the outer part
of the model becomes elongated along the
symmetry axis, which is rather unphysical. For this reason Wilson
considered only values of a at which the second term in the
exponent of Equation (22) was comparatively unimportant.
It is a pity that a distribution function has not been devised that
generates
models with isodensity surfaces whose ellipticity is nearly independent of
radius and whose rotation curves are correspondingly flat. This is
because the observations of early-type disk galaxies (see below)
indicate that the spheroidal components of these galaxies have such
characteristics. A device that was introduced by
Lynden-Bell (1962a)
and improved by
Hunter (1975) might
be employed to guide one in the choice of a more appropriate distribution
function. Lynden-Bell showed how, given the density distribution of a
galaxy having
f (E, Jz), one may recover the part
f+ of f that is even in
Jz. The part f_ that is odd in
Jz cannot be recovered from
(R,
z), but it is possible that it is determined by
<v>(R, z) . In either of its
present forms, Lynden-Bell's technique requires that
(R,
z) be extended to a complex analytic function of
R and 
, which
makes the method difficult to formulate
numerically and has until now restricted the technique to rather
unrealistic density distributions.
An interesting application of Lynden-Bell's device is found in the work of Lake (1981a, b) on prolate galaxies. Lake first recovered the f+(E, Jz) that generates a type of prolate Plummer model. In these models the density is infinite on the symmetry axis of the system, and this is reflected in f+ containing a Dirac delta-function of Jz. Lake modified f+ by smearing the delta-function out into a peak of finite width, and then solved for the density structure associated with the modified form of f+ using the methods employed by PT. In this way he obtained a prolate model whose density is nowhere infinite. This model is probably of only academic interest, since prolate galaxies are very unlikely to have <vR2> = <vz2>, but it is a nice illustration of how Lynden-Bell's device may be profitably employed in the future.
The problem of constructing general axisymmetric models in which
f = f (E, Jz) and
<vR2>
<vz2>, as is required by observations
of the galactic
halo, will normally take one beyond the range of validity of Jeans' theorem
because it requires that one take into account the complexities to which
the "third integral" gives rise. As indicated in
Section 2, many (perhaps most)
orbits in a reasonably smooth potential respect three isolating
integrals, which in an axisymmetric potential we may denote
E, Jz and I3. If one knew the
analytic form of
I3(x, v;
) , one might construct
models by treating it on a par with E and Jz
(Lynden-Bell 1962b).
But a simple expression does not exist for
I3, even for the regular orbits, and Jeans' theorem
breaks down soon when orbits exist that are neither ergodic nor regular.
Schwarzschild (1979)
has developed a technique for constructing
self-consistent models around a given density distribution that works
even in the presence of irregular orbits. He follows a large number of
orbits in the potential associated with his chosen density distribution
and then uses a linear-programming technique to populate a selection of
these orbits. This is done in
such a way that the time-averaged density contributed by these orbits to
each of a large number of cells throughout the system equals the density
originally assumed. Schwarzschild developed this technique to handle the
difficult problem of constructing triaxial galaxies, but it is eminently
well suited to the construction of general axisymmetric galaxies.
Richstone (1980,
1982)
has employed a variant of this method to build a special type of
axisymmetric
galaxy - that in which the isodensity surfaces are similar spheroids and
~
R-2 . It is to be hoped that more general models of
this type will be constructed in the near future.
Models from moment equations The next best thing to
a solution of the
coupled Vlasov and Poisson equations is information about the relationships
that hold between the velocity moments of a galaxy of given density
distribution.
Satoh (1980)
used the Jeans equations to derive the velocity dispersion
(R, z) and
the rotation speed
<v>(R, z)
of a galaxy of given density on the assumption that the velocity
dispersion in the system is everywhere isotropic.
The density distributions studied by Satoh are modified Plummer models in
which ~
R-3 at large R in the equatorial plane, and
~
z-6 far out along the symmetry axis. The curves of
<v>(R, 0) peak many
core radii from the center and then flatten off until the circular
velocity has fallen to a value nearly equal to
<v>(R, 0). The velocity
dispersion in these models falls steeply with increasing radius.
Binney (1980b)
has applied the tensor virial theorem to the volumes of
systems that are bounded by isodensity surfaces to estimate
<v>(R, 0), using
a number of assumptions about the way in which
<v> varies with R and z
and the degree of anisotropy of the velocity dispersion tensor. The systems
studied included model galaxies in which
~
(R2 + z2 /
q2)-3/2 at large R and
z (q being the axial ratio), and models of three of the
galaxies studied photometrically by
King (1978).
These models suggest that one cannot depress
<v> to the degree that is required by the
observations (see below) unless the
velocity ellipsoids have principal axes that near the center align with
the equatorial plane, rather than with the radial direction. The
rotation curves that
King's galaxies would require if their velocity dispersion tensors were
isotropic rise very steeply near the center and then become remarkably
flat. The velocity dispersion in these galaxies should decline slowly
with increasing radius.
N-body models N-body models are superior even to exact solutions of the Vlasov equation in one important respect: they are easily tested for stability. Against this signal advantage must be set their cumbersomeness and the difficulty encountered by older programs in handling both large numbers of particles and large density contrasts. Fortunately, algorithms have now been developed by (among others) van Albada (1982), Villumsen (1982), and McGlynn & Ostriker (in preparation) that are able to combine the flexibility as regards density contrasts of programs that calculate forces by direct summation over all particles (e.g. Ahmad & Cohen 1973) with the ability of the Fourier approach to the force calculation to handle enormous numbers of particles.
One makes a galaxy model with an N-body code by allowing
particles to relax to a steady state from some initial
configuration. The initial conditions
generally are a homogeneous distribution within some boundary, with a
Gaussian velocity dispersion superposed on some degree of rigid-body
rotation. However, as
Gott (1975)
has emphasized, galaxies are unlikely to have
relaxed from homogeneous initial configurations. This is unfortunate
since the numerical experiments show that the initial conditions from which
relaxation occurs influence the final state.
Gott (1973),
Gott & Thuan (1976),
Miller (1978),
Miller & Smith
(1979),
Hohl & Zang (1979),
van Albada (1982),
and others have studied the collapse of rotating spheres of stars, while
Binney (1976),
Aarseth & Binney
(1978),
and Miller & Smith
(1981)
have studied the collapse of initially flattened
stellar distributions. These investigations show the following. (a)
Systems formed by relaxation from homogeneous initial configurations are
as centrally concentrated as are galaxies only if the initial conditions
are very cold. (b) In
the absence of dynamically significant rotation of the initial state,
initially spherical systems relax to spheres and initially flattened
systems relax to spheroids. (c) The velocity ellipsoids of relaxed
systems have a strong radial
bias in the outer regions, and become in the almost homogeneous core either
isotropic (if the system is spherical) or oblate and aligned with the
figure of
the system (if the system as a whole is flattened). In the latter case,
f f
(E, Jz) .
(d) Rapidly rotating initial configurations form tumbling bars rather
than highly flattened axisymmetric bodies,
Hohl & Zang (1979)
find that the flattest
axisymmetric body that can be formed from a rotating homogeneous stellar
sphere is E2. Axisymmetric bodies of flattening as high as E7 can be formed
by the relaxation of flattened nonrotating initial configurations.
These results indicate that phase mixing and violent relaxation (Lynden-Bell 1967) work too inefficiently to be capable of imposing a uniform stamp on elliptical galaxies. However, the collapse calculations show that plausible initial conditions will lead to the formation of systems that closely resemble the galactic halo and nearby elliptical galaxies.
TRIAXIAL MODELS Collapse calculations of the type just described suggest that triaxiality is likely to be common whether the initial configuration is one of rapid or slow rotation. Indeed if the initial. configuration is not axially symmetric and the rotation of the initial state is dynamically unimportant, it is hard to see what might determine a particular body axis as an axis of symmetry. Aarseth & Binney (1978) and Wilkinson & James (1982) have verified that systems that relax from slowly or nonrotating triaxial configurations do form triaxial galaxies that appear to be long-lived (but see Sanders & van Albada 1979). If, however, the initial state is one of rapid rotation, the system is found to form a tumbling bar that has no axis of symmetry (Miller & Smith 1979, Hohl & Zang 1979).
While it is easy to form individual bars with an N-body program, it is difficult to isolate the general principles of bar dynamics. Schwarzschild's construction of stellar bars from individual orbits in a given potential (1979 and work in progress) helps one come closer to these general principles. This work and that of Wilkinson & James (1982) indicate that the backbone of a slowly rotating stellar bar is a population of stars on orbits that may be considered epicyclic developments of the closed orbit that lies along the long axis of the potential. These orbits may or may not have a definite sense of circulation about the long axis of the system, but they have a definite sense of circulation about either of the shorter axes of the system only if the figure of the potential rotates. Then they circulate with respect to the figure in the same sense as that of the figure with respect to inertial space. This suggests, and the available N-body models confirm, that there is a fairly tight connection between the pattern speed with which the figure of the bar rotates and the speed with which the stars stream with respect to the figure; bars that have large pattern speeds show strong streaming motions with respect to the pattern of the bar. In particular, it should be possible (in principle) to estimate the pattern speed of a bar from a knowledge of the magnitude of the overall circulation and an estimate of the axial ratios of the bar. Conversely, if one can argue that the pattern speed of a particular galaxy must be small, because its brightness profile shows no sign of a characteristic radius where corotation or a Lindblad resonance may occur, it may be possible to use the magnitude of the stellar rotation velocity close to the center of the galaxy to limit the deviation of the figure of the galaxy from axial symmetry.
Resonances are bound to play an important role in the dynamics of triaxial elliptical galaxies, and one would certainly expect the brightness profiles of such galaxies to show features at the characteristic radii of such resonances. It is possibly worth recalling in this connection the elliptical rings that have been found by Malin & Carter (1980) on high-contrast prints of elliptical galaxies.