2.2. Quantum zero-point energy

The introduction of quantum mechanics changes this story somewhat. For one thing, Planck's constant allows us to define a gravitational length scale, the reduced Planck length

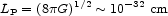(1.6)

as well as the reduced Planck mass

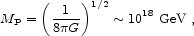(1.7)

where "reduced" means that we have included the 8's where they really should be. (Note that, with = 1 and c = 1, we have L = T = M^-1 = E^-1, where L represents a length scale, T a time interval, M a mass scale, and E an energy.) Hence, there is a natural expectation for the scale of the cosmological constant, namely

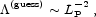(1.8)

or, phrased as an energy density,

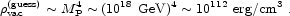(1.9)

We can partially justify this guess by thinking about quantum fluctuations in the vacuum. At all energies probed by experiment to date, the world is accurately described as a set of quantum fields (at higher energies it may become strings or something else). If we take the Fourier transform of a free quantum field, each mode of fixed wavelength behaves like a simple harmonic oscillator. ("Free" means "noninteracting"; for our purposes this is a very good approximation.) As we know from elementary quantum mechanics, the ground-state or zero-point energy of an harmonic oscillator with potential V(x) = 1/2 ² x² is E₀ = 1/2 . Thus, each mode of a quantum field contributes to the vacuum energy, and the net result should be an integral over all of the modes. Unfortunately this integral diverges, so the vacuum energy appears to be infinite. However, the infinity arises from the contribution of modes with very small wavelengths; perhaps it was a mistake to include such modes, since we don't really know what might happen at such scales. To account for our ignorance, we could introduce a cutoff energy, above which we ignore any potential contributions, and hope that a more complete theory will eventually provide a physical justification for doing so. If this cutoff is at the Planck scale, we recover the estimate (1.9).

The strategy of decomposing a free field into individual modes and assigning a zero-point energy to each one really only makes sense in a flat spacetime background. In curved spacetime we can still "renormalize" the vacuum energy, relating the classical parameter to the quantum value by an infinite constant. After renormalization, the vacuum energy is completely arbitrary, just as it was in the original classical theory. But when we use general relativity we are really using an effective field theory to describe a certain limit of quantum gravity. In the context of effective field theory, if a parameter has dimensions [mass]ⁿ, we expect the corresponding mass parameter to be driven up to the scale at which the effective description breaks down. Hence, if we believe classical general relativity up to the Planck scale, we would expect the vacuum energy to be given by our original guess (1.9).

However, we believe we have now measured the vacuum energy through a combination of Type Ia supernovae (Riess et al. 1998, Perlmutter et al. 1999, Tonry et al. 2003, Knop et al. 2003), microwave background anisotropies (Spergel et al. 2003), and dynamical matter measurements (Verde et al. 2002), to reveal

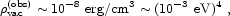(1.10)

or

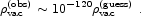(1.11)

For reviews see Sahni and Starobinski 2000, Carroll 2001, or Peebles and Ratra 2003.

Clearly, our guess was not very good. This is the famous 120-orders-of-magnitude discrepancy that makes the cosmological constant problem such a glaring embarrassment. Of course, it is somewhat unfair to emphasize the factor of 10¹²⁰, which depends on the fact that energy density has units of [energy]⁴. We can express the vacuum energy in terms of a mass scale,

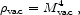(1.12)

so our observational result is

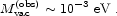(1.13)

The discrepancy is thus

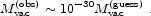(1.14)

We should think of the cosmological constant problem as a discrepancy of 30 orders of magnitude in energy scale.