Why is the Universe Accelerating?

2.3. The coincidence scandal

The third issue mentioned above is the coincidence between the observed vacuum energy (1.11) and the current matter density. To understand this, we briefly review the dynamics of an expanding Robertson-Walker spacetime. The evolution of a homogeneous and isotropic universe is governed by the Friedmann equation,

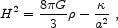(1.15)

where a(t) is the scale factor, H = dot{a} / a is the Hubble parameter, rho is the energy density, and kappa is the spatial curvature parameter. The energy density is a sum of different components, rho = sum _i rho _i, which will in general evolve differently as the universe expands. For matter (non-relativistic particles) the energy density goes as rho _M propto a^-3, as the number density is diluted with the expansion of the universe. For radiation the energy density goes as rho _R propto a^-4, since each particle loses energy as it redshifts in addition to the decrease in number density. Vacuum energy, meanwhile, is constant throughout spacetime, so that rho propto a⁰.

It is convenient to characterize the energy density of each component by its density parameter

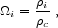(1.16)

where the critical density

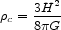(1.17)

is that required to make the spatial geometry of the universe be flat ( kappa = 0). The "best-fit universe" or "concordance" model implied by numerous observations includes radiation, matter, and vacuum energy, with

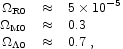(1.18)

together implying a flat universe. We see that the densities in matter and vacuum are of the same order of magnitude. ⁽²⁾ But the ratio of these quantities changes rapidly as the universe expands:

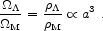(1.19)

As a consequence, at early times the vacuum energy was negligible in comparison to matter and radiation, while at late times matter and radiation are negligible. There is only a brief epoch of the universe's history during which it would be possible to witness the transition from domination by one type of component to another. This is illustrated in Figure 1, in which the various density parameters Omega _i are plotted as a function of the scale factor. At early times Omega _R is close to unity; the matter-radiation transition happens relatively gradually, while the matter-vacuum transition happens quite rapidly.

Figure 1. Density parameters Omega _i for radiation (R), matter (M), and vacuum ( Lambda ), as a function of the scale factor a, in a universe with Omega ₀ = 0.7, Omega _{M 0} = 0.3, Omega _{R 0} = 5 × 10^-5. Scale factors corresponding to the Planck era, electroweak symmetry breaking (EW), and Big Bang nucleosynthesis (BBN) are indicated, as well as the present day.

How finely-tuned is it that we exist in the era when vacuum and matter are comparable? Between the Planck time and now, the universe has expanded by a factor of approximately 10³². To be fair, we should consider an interval of logarithmic expansion which is centered around the present time; this would describe a total expansion by a factor of 10⁶⁴. If we take the transitional period between matter and vacuum to include the time from / _M = 0.1 to / _M = 10, the universe expands by a factor of 100^1/3 10^0.67. Thus, there is an approximately 1% chance that an observer living in a randomly selected logarithmic expansion interval in the history of our universe would be lucky enough to have _M and be the same order of magnitude. Everyone will have their own favorite way of quantifying such unnaturalness, but the calculation here gives some idea of the fine-tuning involved; it is substantial, but not completely ridiculous.

As we will discuss below, there is room to imagine that we are actually not observing the effects of an ordinary cosmological constant, but perhaps a dark energy source that varies gradually as the universe expands, or even a breakdown of general relativity on large scales. By itself, however, making dark energy dynamical does not offer a solution to the coincidence scandal; purely on the basis of observations, it seems clear that the universe has begun to accelerate recently, which implies a scale at which something new is kicking in. In particular, it is fruitless to try to explain the matter/dark energy coincidence by invoking mechanisms which make the dark energy density time-dependent in such a way as to always be proportional to that in matter. Such a scenario would either imply that the dark energy would redshift away as _dark a^-3, which from (1.15) would lead to a non-accelerating universe, or require departures from conventional general relativity of the type which (as discussed below) are excluded by other measurements.

² Of course the "matter" contribution consists both of ordinary baryonic matter and non-baryonic dark matter, with Omega _b approx 0.04 and Omega _DM approx 0.25. The similarity between these apparently-independent quantities is another coincidence problem, but at least one which is independent of time; we have nothing to say about it here. Back.