3.2. Is general relativity breaking down?

If we believe that we live in a universe which is homogeneous, isotropic, and accelerating, general relativity (GR) is unambiguous about the need for some sort of dark energy source. GR has been fantastically successful in passing classic experimental tests in the solar system, as well as at predicting the amount of gravitational radiation emitted from the binary pulsar (Will 2001). Nevertheless, the possibility remains open that gravitation might deviate from conventional GR on scales corresponding to the radius of the entire universe. For our present purposes, such deviations may either be relevant to the cosmological constant problem, or to the dark energy puzzle.

The idea behind modifying gravity to address the cosmological constant problem is to somehow allow for the vacuum energy to be large, but yet not lead to an appreciable spacetime curvature (as manifested in a rapidly expanding universe). Of course we still need to allow ordinary matter to warp spacetime, so there has to be something special about vacuum energy. One special thing is that vacuum energy comes with a negative pressure p_vac = - _vac, as in (1.4). We might therefore imagine a theory which gave rise to a modified version of the Friedmann equation, of the form

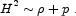(1.20)

With such an equation, ordinary matter (for which p vanishes) leads to conventional expansion, while vacuum energy decouples entirely. Such a theory has been studied (Carroll & Mersini 2001), and may even arise in "self-tuning" models of extra dimensions (Arkani-Hamed, Dimopoulos, Kaloper & Sundrum, 2000, Kachru, Schulz & Silverstein 2000). Unfortunately, close examination of self-tuning models reveals that there is a hidden fine-tuning, expressed as a boundary condition chosen at a naked singularity in the extra dimension. Furthermore, any alternative to the conventional Friedmann equation is also constrained by observations: any alternative must predict the right abundances of light elements from Big Bang nucleosynthesis (BBN; see Burles, Nollett, & Turner 2001), the correct evolution of a sensible spectrum of primordial density fluctuations into the observed spectrum of temperature anisotropies in the Cosmic Microwave Background and the power spectrum of large-scale structure (Tegmark 2002, Zahn & Zaldarriaga 2003, Lue, Scoccimarro & Starkman 2003), and that the age of the universe is approximately thirteen billion years. The most straightforward test comes from BBN (Carroll & Kaplinghat 2002, Masso & Rota 2003), since the light-element abundances depend on the expansion rate during a relatively brief period (rather than on the behavior of perturbations, or an an integral of the expansion rate over a long period). Studies of BBN in alternate cosmologies indicate that it is possible for modifications of GR to remain consistent with observations, but only for a very narrow set of possibilities. It seems likely that the success of conventional BBN, including its agreement with the baryon density as determined by CMB fluctuations (Spergel et al. 2003), is not a misleading accident, but rather an indication that GR provides an accurate description of cosmology when the universe was of the order of one minute old. The idea of modifying GR to solve the cosmological constant problem is not completely dead, but is evidently not promising.

Rather than trying to solve the cosmological constant problem, we can put aside the issue of why the magnitude of the vacuum energy is small and focus instead on whether the current period of acceleration can be traced to a modification of GR. A necessary feature of any such attempt is to include a new scale in the theory, since acceleration has only begun relatively recently. ⁽³⁾ From a purely phenomenological point of view we can imagine modifying the Friedmann equation (1.15) so that acceleration kicks in when either the energy density approaches a certain value _*,

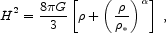(1.21)

or when the Hubble parameter approaches a certain value H_*,

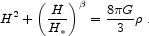(1.22)

The former idea has been suggested by Freese & Lewis 2002, the latter by Dvali & Turner 2003; in both cases we can fit the data for appropriate choices of the new parameters. It is possible that equations of this type arise in brane-world models with large extra spatial dimensions; it is less clear whether the appropriate parameters can be derived. An even more dramatic mechanism also takes advantage of extra dimensions, but allows for separate gravitational dynamics on and off of our brane; in this case gravity can be four-dimensional below a certain length scale (which would obviously have to be very large), and appear higher-dimensional at large distances (Dvali, Gabadadze & Porrati 2000, Deffayet, Dvali, & Gabadadze 2002, Arkani-Hamed, Dimopoulos, Dvali & Gabadadze 2002). These scenarios can also make the universe accelerate at late times, and may even lead to testable deviations from GR in the solar system (Dvali, Gruzinov, & Zaldarriaga 2003; Lue and Starkman 2003).

As an alternative to extra dimensions, we may look for an ordinary four-dimensional modification of GR. This would be unusual behavior, as we are used to thinking of effective field theories as breaking down at high energies and small length scales, but being completely reliable in the opposite regime. Nevertheless, it is worth exploring whether a simple phenomenological model can easily accommodate the data. Einstein's equation can be derived by minimizing an action given by the spacetime integral of the curvature scalar R,

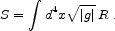(1.23)

A simple way to modify the theory when the curvature becomes very small (at late times in the universe) is to simply add a piece proportional to 1/R,

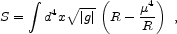(1.24)

where µ is a parameter with dimensions of mass (Carroll, Duvvuri, Trodden and Turner 2003). It is straightforward to show that this theory admits accelerating solutions; unfortunately, it also brings to life a new scalar degree of freedom, which may ruin the success of GR in the solar system (Chiba 2003). Investigations are still ongoing to see whether a simple modification of this idea could explain the acceleration of the universe while remaining consistent with experimental tests; in the meantime, the difficulty in finding a simple extension of GR that does away with the cosmological constant provides yet more support for the standard scenario.

³ One way of characterizing this scale is in terms of the Hubble parameter when the universe starts accelerating, H₀ ~ 10^-18 sec^-1. It is interesting in this context to recall the coincidence pointed out by Milgrom (1983), that dark matter only becomes important in galaxies when the acceleration due to gravity dips below a fixed value, a₀ / c 10^-18 sec^-1. Milgrom himself has suggested that the explanation for this feature of galactic dynamics can be explained by replacing dark matter by a modified dynamics, and it is irresistible to speculate that both dark matter and dark energy could be replaced by a single (as yet undiscovered) modified theory of gravity. However, hope for this possibility seems to be gradually becoming more difficult to maintain, as different methods indicate the existence of gravitational forces which point in directions other than where ordinary matter is (Van Waerbeke et al. 2000, Dalal & Kochanek 2002, Kneib et al. 2003) - a phenomenon that is easy to explain with dark matter, but difficult with modified gravity - and explanations are offered for a₀ / c ~ H₀ within conventional cold dark matter (Scott, White, Cohn, & Pierpaoli 2001, Kaplinghat & Turner 2002). Back.