3.3. Is dark energy dynamical?

If general relativity is correct, cosmic acceleration implies there must be a dark energy density which diminishes relatively slowly as the universe expands. This can be seen directly from the Friedmann equation (1.15), which implies

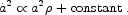(1.25)

From this relation, it is clear that the only way to get acceleration ( increasing) in an expanding universe is if falls off more slowly than a^-2; neither matter (_M a^-3) nor radiation (_R a^-4) will do the trick. Vacuum energy is, of course, strictly constant; but the data are consistent with smoothly-distributed sources of dark energy that vary slowly with time.

There are good reasons to consider dynamical dark energy as an alternative to an honest cosmological constant. First, a dynamical energy density can be evolving slowly to zero, allowing for a solution to the cosmological constant problem which makes the ultimate vacuum energy vanish exactly. Second, it poses an interesting and challenging observational problem to study the evolution of the dark energy, from which we might learn something about the underlying physical mechanism. Perhaps most intriguingly, allowing the dark energy to evolve opens the possibility of finding a dynamical solution to the coincidence problem, if the dynamics are such as to trigger a recent takeover by the dark energy (independently of, or at least for a wide range of, the parameters in the theory). To date this hope has not quite been met, but dynamical mechanisms at least allow for the possibility (unlike a true cosmological constant).

The simplest possibility along these lines involves the same kind of source typically invoked in models of inflation in the very early universe: a scalar field rolling slowly in a potential, sometimes known as "quintessence" (Peebles & Ratra 1988, Ratra & Peebles 1988, Wetterich 1998, Frieman, Hill & Watkins 1992, Frieman, Hill, Stebbins & Waga 1995, Caldwell, Dave & Steinhardt 1998, Huey, Wang, Dave, Caldwell & Steinhardt 1999). ⁽⁴⁾ The energy density of a scalar field is a sum of kinetic, gradient, and potential energies,

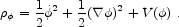(1.26)

For a homogeneous field ( 0), the equation of motion in an expanding universe is

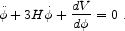(1.27)

If the slope of the potential V is quite flat, we will have solutions for which is nearly constant throughout space and only evolving very gradually with time; the energy density in such a configuration is

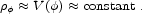(1.28)

Thus, a slowly-rolling scalar field is an appropriate candidate for dark energy.

However, introducing dynamics opens up the possibility of introducing new problems, the form and severity of which will depend on the specific kind of model being considered. Most quintessence models feature scalar fields with masses of order the current Hubble scale,

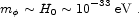(1.29)

(Fields with larger masses would typically have already rolled to the minimum of their potentials.) In quantum field theory, light scalar fields are unnatural; renormalization effects tend to drive scalar masses up to the scale of new physics. The well-known hierarchy problem of particle physics amounts to asking why the Higgs mass, thought to be of order 10¹¹ eV, should be so much smaller than the grand unification/Planck scale, 10²⁵-10²⁷ eV. Masses of 10^-33 eV are correspondingly harder to understand. (Strategies toward understanding include approximate global symmetries, discussed in section 4.2, and large kinetic-term renormalizations, as suggested by Dimopulos & Thomas 2003.)

Nevertheless, this apparent fine-tuning might be worth the price, if we were somehow able to explain the coincidence problem. To date, many investigations have considered scalar fields with potentials that asymptote gradually to zero, of the form e^{1 /} or 1 / . These can have cosmologically interesting properties, including "tracking" behavior that makes the current energy density largely independent of the initial conditions (Zlatev, Wang & Steinhardt 1999). They do not, however, provide a solution to the coincidence problem, as the era in which the scalar field begins to dominate is still set by finely-tuned parameters in the theory. One way to address the coincidence problem is to take advantage of the fact that matter/radiation equality was a relatively recent occurrence (at least on a logarithmic scale); if a scalar field has dynamics which are sensitive to the difference between matter- and radiation-dominated universes, we might hope that its energy density becomes constant only after matter/radiation equality. An approach which takes this route is k-essence (Armendariz-Picon, Mukhanov & Steinhardt 2000), which modifies the form of the kinetic energy for the scalar field. Instead of a conventional kinetic energy K = 1/2 ()², in k-essence we posit a form

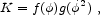(1.30)

where f and g are functions specified by the model. For certain choices of these functions, the k-essence field naturally tracks the evolution of the total radiation energy density during radiation domination, but switches to being almost constant once matter begins to dominate. Unfortunately, it seems necessary to choose a finely-tuned kinetic term to get the desired behavior (Malquarti, Copeland, & Liddle 2003).

An alternative possibility is that there is nothing special about the present era; rather, acceleration is just something that happens from time to time. This can be accomplished by oscillating dark energy (Dodelson, Kaplinghat & Stewart 2000). In these models the potential takes the form of a decaying exponential (which by itself would give scaling behavior, so that the dark energy remained proportional to the background density) with small perturbations superimposed:

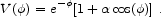(1.31)

On average, the dark energy in such a model will track that of the dominant matter/radiation component; however, there will be gradual oscillations from a negligible density to a dominant density and back, on a timescale set by the Hubble parameter, leading to occasional periods of acceleration. In the previous section we mentioned the success of the conventional picture in describing primordial nucleosynthesis (when the scale factor was a_BBN ~ 10^-9) and temperature fluctuations imprinted on the CMB at recombination (a_CMB ~ 10^-3), which implies that the oscillating scalar must have had a negligible density during those periods; but explicit models are able to accommodate this constraint. Unfortunately, in neither the k-essence models nor the oscillating models do we have a compelling particle-physics motivation for the chosen dynamics, and in both cases the behavior still depends sensitively on the precise form of parameters and interactions chosen. Nevertheless, these theories stand as interesting attempts to address the coincidence problem by dynamical means.

⁴ While the potential energy of a light scalar field is the most straightforward candidate for dynamical dark energy, it is by no means the only possibility. Other models included tangled topological defects (Vilenkin 1984, Spergel & Pen 1997, Battye, Bucher & Spergel 1999, Friedland, Murayama & Perelstein 2003), curved-spacetime renormalization effects (Sahni & Habib 1998, Parker & Raval 1999), trans-planckian vacuum modes (Mersini, Bastero-Gil and Kanti 2001, Bastero-Gil & Mersini 2002, Lemoine, Martin & Uzan 2003), and Chaplygin gasses (Kamenshchik, Moschella & Pasquier 2001). Back.