3.4. Did we just get lucky?

By far the most straightforward explanation for the observed acceleration of the universe is an absolutely constant vacuum energy, or cosmological constant. Even in this case we can distinguish between two very different scenarios: one in which the vacuum energy is some fixed number that as yet we simply don't know how to calculate, and an alternative in which there are many distinct domains in the universe, with different values of the vacuum energy in each. In this section we concentrate on the first possibility. Note that such a scenario requires that we essentially give up on finding a dynamical resolution to the coincidence scandal; instead, the vacuum energy is fixed once and for all, and we are simply fortunate that it takes on a sufficiently gentle value that life has enough time and space to exist.

To date, there are not any especially promising approaches to calculating the vacuum energy and getting the right answer; it is nevertheless instructive to consider the example of supersymmetry, which relates to the cosmological constant problem in an interesting way. Supersymmetry posits that for each fermionic degree of freedom there is a matching bosonic degree of freedom, and vice-versa. By "matching" we mean, for example, that the spin-1/2 electron must be accompanied by a spin-0 "selectron" with the same mass and charge. The good news is that, while bosonic fields contribute a positive vacuum energy, for fermions the contribution is negative. Hence, if degrees of freedom exactly match, the net vacuum energy sums to zero. Supersymmetry is thus an example of a theory, other than gravity, where the absolute zero-point of energy is a meaningful concept. (This can be traced to the fact that supersymmetry is a spacetime symmetry, relating particles of different spins.)

We do not, however, live in a supersymmetric state; there is no selectron with the same mass and charge as an electron, or we would have noticed it long ago. If supersymmetry exists in nature, it must be broken at some scale M_SUSY. In a theory with broken supersymmetry, the vacuum energy is not expected to vanish, but to be of order

(1.32)

with _vac = M_vac⁴. What should M_SUSY be? One nice feature of supersymmetry is that it helps us understand the hierarchy problem - why the scale of electroweak symmetry breaking is so much smaller than the scales of quantum gravity or grand unification. For supersymmetry to be relevant to the hierarchy problem, we need the supersymmetry-breaking scale to be just above the electroweak scale, or

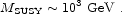(1.33)

In fact, this is very close to the experimental bound, and there is good reason to believe that supersymmetry will be discovered soon at Fermilab or CERN, if it is connected to electroweak physics.

Unfortunately, we are left with a sizable discrepancy between theory and observation:

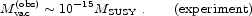(1.34)

Compared to (1.14), we find that supersymmetry has, in some sense, solved the problem halfway (on a logarithmic scale). This is encouraging, as it at least represents a step in the right direction. Unfortunately, it is ultimately discouraging, since (1.14) was simply a guess, while (1.34) is actually a reliable result in this context; supersymmetry renders the vacuum energy finite and calculable, but the answer is still far away from what we need. (Subtleties in supergravity and string theory allow us to add a negative contribution to the vacuum energy, with which we could conceivably tune the answer to zero or some other small number; but there is no reason for this tuning to actually happen.)

But perhaps there is something deep about supersymmetry which we don't understand, and our estimate M_vac ~ M_SUSY is simply incorrect. What if instead the correct formula were

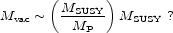(1.35)

In other words, we are guessing that the supersymmetry-breaking scale is actually the geometric mean of the vacuum scale and the Planck scale. Because M_P is fifteen orders of magnitude larger than M_SUSY, and M_SUSY is fifteen orders of magnitude larger than M_vac, this guess gives us the correct answer! Unfortunately this is simply optimistic numerology; there is no theory that actually yields this answer (although there are speculations in this direction; Banks 2003). Still, the simplicity with which we can write down the formula allows us to dream that an improved understanding of supersymmetry might eventually yield the correct result.

Besides supersymmetry, we do know of other phenomena which may in principle affect our understanding of vacuum energy. One example is the idea of large extra dimensions of space, which become possible if the particles of the Standard Model are confined to a three-dimensional brane (Arkani-Hamed, Dimopoulos & Dvali 1998, Randall & Sundrum 1999). In this case gravity is not simply described by four-dimensional general relativity, as alluded to in the previous section. Furthermore, current experimental bounds on simple extra-dimensional models limit the scale characterizing the extra dimensions to less than 10^-2 cm, which corresponds to an energy of approximately 10^-3 eV; this is coincidentally the same as the vacuum-energy scale (1.10). As before, nobody has a solid reason why these two scales should be related, but it is worth searching for one. The fact that we are forced to take such slim hopes seriously is a measure of how difficult the cosmological constant problem really is.