2. WHAT IS IT?

As discussed here by Kolb (2003), particle candidates for dark matter range from the axion with a mass 10^-15 GeV (van Bibber 2003) to cryptons with masses 10⁺¹⁵ GeV (Ellis et al. 1990; Benakli et al. 1999), via neutrinos with masses 10^-10 GeV, the gravitino and the lightest supersymmetric particle with a mass 10² GeV (Ellis et al. 1984; Goldberg 1983). In recent years, there has been considerable experimental progress in understanding neutrino masses, so I start with them, even though cosmology now disfavours the hot dark matter they would provide (Spergel et al. 2003). All the others are candidates for cold dark matter, except for the gravitino, which might constitute warm dark matter, another possibility now disfavoured by the WMAP evidence for reionization when z ~ 20 (Kogut et al. 2003).

2.1. Neutrinos

Particle theorists expect particles to have masses that vanish exactly only if they are protected by some unbroken gauge symmetry, much as the photon is massless because of the U(1) gauge symmetry of electromagnetism, that is associated with the conservation of electric charge. There is no corresponding exact gauge symmetry to protect lepton number, so we expect it to be violated and neutrinos to acquire masses. This is indeed the accepted interpretation of the observed oscillations between different types of neutrinos, which are made possible by mixing into non-degenerate mass eigenstates (Wark 2003); Pakvasa & Valle 2003).

Neutrino masses could arise even within the Standard Model of particle physics, without adding any new particles, at the expense of introducing a interaction between two neutrino fields and two Higgs fields (Barbieri et al. 1980):

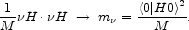(2.1)

However, such an interaction would be non-renormalizable, and therefore is not thought to be fundamental. The (presumably large) mass scale M appearing the denominator of (2.1) is generally thought to originate from the exchange of some massive fermionic particle that mixes with the light neutrino (Gell-Mann et al. 1979; Yanagida 1979; Mohapatra & Senjanovic 1980):

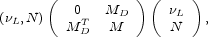(2.2)

Diagonalization of this matrix naturally yields small neutrino masses, since we expect that the Dirac mass term m_D is of the same order as quark and lepton masses, and M >> m_W.

We have the following direct experimental upper limits on neutrino masses. From measurements of the end-point in Tritium decay, we know that (Weinheimer et al. 1999; Lobashev et al. 1999):

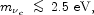(2.3)

and there are prospects to improve this limit down to about 0.5 eV with the proposed KATRIN experiment (Osipowicz et al. 2001). From measurements of µ decay, we know that (Hagiwara et al. 2002):

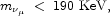(2.4)

and there are prospects to improve this limit by a factor ~ 20. From measurements of n decay, we know that (Hagiwara et al. 2002):

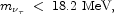(2.5)

and there are prospects to improve this limit to ~ 5 MeV.

However, the most stringent laboratory limit on neutrino masses may come from searches for neutrinoless double- decay, which constrain the sum of the neutrinos' Majorana masses weighted by their couplings to electrons (Klapdor-Kleingrothaus et al. 2001):

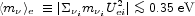(2.6)

and there are prospects to improve this limit to ~ 0.01 eV in a future round of experiments. The impact of the limit (2.6) in relation to the cosmological upper limit (1.1) is discussed below, after we have gathered further experimental input from neutrino-oscillation experiments.

The neutrino mass matrix (2.2) should be regarded also as a matrix in flavour space. When it is diagonalized, the neutrino mass eigenstates will not, in general, coincide with the flavour eigenstates that partner the mass eigenstates of the charged leptons. The mixing matrix between them (Maki et al. 1962) may be written in the form

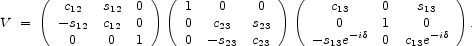(2.7)

where the symbols c, s_ij denote the standard trigonometric functions of the three real `Euler' mixing angles _12,23,31, and is a CP-violating phase that can in principle also be observed in neutrino-oscillation experiments (De Rújula et al. 1999). Additionally, there are two CP-violating phases _1,2 that appear in the double- observable (2.6), but do not affect neutrino oscillations.

The pioneering Super-Kamiokande and other experiments have shown that atmospheric neutrinos oscillate, with the following difference in squared masses and mixing angle (Fukuda et al. 1998):

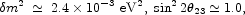(2.8)

which is very consistent with the K2K reactor neutrino experiment (Ahn et al. 2002), as seen in the left panel of Fig. 6. A flurry of recent solar neutrino experiments, most notably SNO (Ahmad et al. 2002a, b), have established beyond any doubt that they also oscillate, with

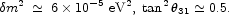(2.9)

Most recently, the KamLAND experiment has reported a deficit of electron antineutrinos from nuclear power reactors, leading to a very similar set of preferred parameters, as seen in the right panel of Fig. 6 (Eguchi et al. 2003).

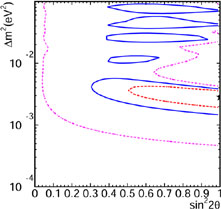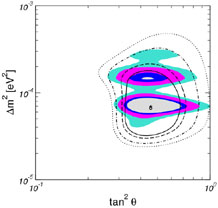Figure 6. Left panel: The region of neutrino oscillation parameters (sin2 2, m2) inferred from the K2K reactor experiment (Ahn et al. 2002) includes the central values favoured by the Super-Kamiokande atmospheric-neutrino experiment, indicated by the star (Fukuda et al. 1998). Right panel: The region of neutrino oscillation parameters (tan2 , m2) inferred from solar-neutrino experiments is very consistent with derived from the KamLAND reactor neutrino experiment (Eguchi et al. 2003). The shaded regions show the combined probability distribution (Pakvasa & Valle, 2003).

Using the range of ₁₂ allowed by the solar and KamLAND data, one can establish a correlation between the relic neutrino density h² and the neutrinoless double- decay observable <m>_e, as seen in Fig. 7 (Minakata & Sugiyama 2002). Pre-WMAP, the experimental limit on <m>_e could be used to set the bound (Minakata & Sugiyama 2002)

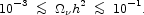(2.10)

Alternatively, now that WMAP has set a tighter upper bound h² < 0.0076 (1.1), one can use this correlation to set an upper bound:

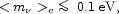(2.11)

which is difficult to reconcile with the signal reported in (Klapdor-Kleingrothaus et al. 2002).

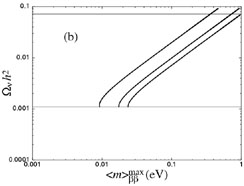Figure 7. Correlation between h2 and <m>e. The different diagonal lines correspond to uncertainties in the measurements by KamLAND and other experiments (Minakata & Sugiyama 2002).

The `Holy Grail' of neutrino physics is CP violation in neutrino oscillations, which would manifest itself as a difference between the oscillation probabilities for neutrinos and antineutrinos (De Rújula et al. 1999):

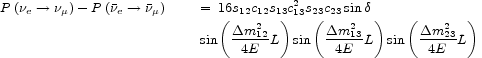(2.12)

For this to be observable, m₁₂ and ₁₂ have to be large, as SNO and KamLAND have shown to be the case, and also ₁₃ has to be large enough - which remains to be seen.

In fact, even the minimal seesaw model contains many additional parameters that are not observable in neutrino oscillations (Casas & Ibarra 2001). In addition to the three masses of the charged leptons, there are three light-neutrino masses, three light-neutrino mixing angles and three CP-violating phases in the light-neutrino sector: the oscillation phase and the two Majorana phases that are relevant to neutrinoless double- decay experiments. As well, there are three heavy singlet-neutrino masses, three more mixing angles and three more CP-violating phases that become observable in the heavy-neutrino sector, making a total of 18 parameters. Out of all these parameters, so far just four light-neutrino parameters are known, two differences in masses squared and two real mixing angles.

As discussed later, it is often thought that there may be a connection between CP violation in the neutrino sector and the baryon density in the Universe, via leptogenesis. Unfortunately, this connection is somewhat indirect, since the three CP-violating phases measurable in the light-neutrino sector to not contribute to leptogenesis, which is controlled by the other phases that are not observable directly at low energies (Ellis & Raidal 2002). However, if the seesaw model is combined with supersymmetry, these extra phases contribute to the renormalization of soft superymmetry-breaking parameters at low energies, and hence may have indirect observable effects (Ellis et al. 2002a, b).