The inventory in Table 1 assumes
the now standard relativistic Friedmann-Lemaître
CDM cosmology, in
which space sections at fixed world time have negligibly small mean
curvature, Einstein's cosmological term,
, is independent
of time and position, the
dark matter is an initially cold noninteracting gas, and primeval
departures from homogeneity are adiabatic, Gaussian, and
scale-invariant. Physics in the dark sector is not well constrained:
might be replaced
with a dynamical component, as in the
models for dark energy now under discussion, the physics of the dark
matter may prove to be more complicated than that of a free
collisionless gas, and the initial conditions may not be adequately
approximated by the present standard cosmology. If such complications
were present we expect their effects on entries that are sensitive to
the cosmological model would be slight, however, because the
cosmological tests now offer close to compelling evidence that the
CDM model is a
useful approximation to reality
(Bennett et al. 2003a;
Spergel et al. 2003;
Tegmark et al. 2004a;
and references therein).
To help simplify the discussion we adopt a nominal distance scale, corresponding to Hubble's constant 2
 |
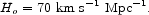(1) |
The energy density,
i, in the form of component i is
expressed as a density parameter,
 |
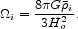(2) |
Since Ho is at best measured to ten percent accuracy (Freedman et al. 2001), an improved distance scale could produce noticeable revisions to the inventory.
The second column from the right in Table 1 lists the density parameters in the components, and the last column presents the total for each category. Both columns sum to unity. Where we state an uncertainty the range spans our estimates of the smallest and largest credible values. The uncertainties in entries 2.1 and 2.3 are too small to be interesting for the purpose of this inventory. Elsewhere the absence of an error flag means the uncertainty is not well documented. In these cases we present numerical values to ± 0.1 dex, but the uncertainty generally is no less than ± 0.3 dex, that is, a factor of two.
2 We also write Ho = 100 h km s-1 Mpc-1, where convenient, but all entries in the inventory in Table 1 assume h = 0.7. Back.