2.1. The Dark Sector

The components in category 1 interact with the contents of the visible sector only by gravity, as far as is now known. This makes it difficult to check whether the dark energy - or Einstein's cosmological constant, - and the dark matter really have the simple properties assumed in the CDM cosmology. Future versions of the inventory might contain separate entries for the potential, kinetic and gradient contributions to the dark energy density, or a potential energy component in the dark matter.

There is abundant evidence that the total mass density - excluding dark energy - is well below the Einstein-de Sitter value. That means, among other things, that the consistency of cross-checks from the many ways to estimate the mass density provides close to compelling evidence that the gravitational interaction of matter at distances up to the large-scale flows is well approximated by the inverse square law, and that starlight is a good tracer of the mass distribution on scales 100 kpc (Peebles 1986; Bahcall, Lubin & Dorman 1995; Fukugita 2001; Percival et al. 2001; Lahav et al. 2002; Verde et al. 2002; Peebles & Ratra 2003; Bennett et al. 2003a; Tegmark et al. 2004a, and references therein).

An example that illustrates the situation, and will be used later, is the estimate from weak lensing of the mean galaxy surface mass density contrast,

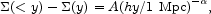(3)

where (y) is the ensemble average surface mass density at projected distance y from a galaxy and ( < y) is the mean surface density within distance y. The measurements by McKay et al. (2001) yield A = 2.5_-0.8^+0.7 h m pc^-2 and = - 0.8± 0.2, and they indicate that the power law is a good approximation to the measurements in the range of projected radii

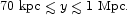(4)

If the galaxy autocorrelation function,

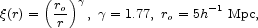(5)

is a good approximation to the galaxy-mass cross correlation function on the range of scales in equation (4), then the mean surface density is

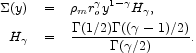(6)

This agrees with equation (3) if the density parameter belonging to the mean density _m of the mass that clusters with the galaxies is

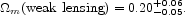(7)

This is in the range of estimates of the value of this parameter now under discussion, consistent with the assumption that galaxies are useful tracers of mass.

Our adopted value for the total mass density in nonrelativistic matter,

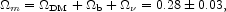(8)

is in the current range of generally accepted values and uncertainties. Equation (8) is based on the WMAP measurement of the anisotropy of the 3 K radiation with the SDSS measurement of the large-scale galaxy correlation function (Spergel et al. 2003; Tegmark et al. 2004a). The galaxy power spectrum from the 2dF redshift survey is somewhat larger than from SDSS on small scales. This would suggest a value closer to _m 0.2 (Percival et al. 2001; Peacock, private communication). The same is true of some dynamical estimates of _m. There is thus the possibility of further adjustment of this important parameter beyond the error flag in equation (8).

We make use of the fact that equation (3) is close to the limiting isothermal sphere mass distribution,

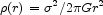(9)

If we connect this form to the power law in equation (5) at the nominal virial radius r_v defined by ( < r_v) / _c = 200, we obtain

(10)

This measure of the characteristic one-dimensional velocity dispersion, , in luminous galaxies agrees with the mean in quadrature,

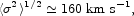(11)

weighted by the FHP morphology fractions, of the dispersions = 225 km s^-1 for elliptical galaxies, = 206 km s^-1 for S0 galaxies (de Vaucouleurs & Olson 1982) and = 130 km s^-1 for spiral galaxies (Sakai et al. 2000), all at luminosity L_B = L_B^*. The isothermal sphere model defines a characteristic mass M_v within r_v. The ratio of M_v to the characteristic galaxy luminosity (eq. [(53] below) is

(12)

in Solar units. The product of M_v with the effective number density of luminous (L^*) galaxies, n_g = 0.017 h³ Mpc^-3 (eq [52]), gives an estimate that the mean mass fraction within the virial radii of the large galaxies,

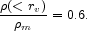(13)

That is, we estimate that about 60% of the dark matter is gathered within the virialized parts of normal galaxies.

Entry 1.3 assumes inflation has produced gravitational waves with a scale-invariant spectrum, meaning the strain appearing at the Hubble length is independent of epoch. The density parameter associated with gravitational waves with wavelengths on the order of the Hubble length is _g ~ ², and the absence of an appreciable effect of gravitational waves on the anisotropy of the 3 K thermal cosmic background radiation indicates 10^-5. The gravitational waves produced by cosmic phase transitions, if detected or convincingly predicted, might be entered in this category. Gravitational waves from the relativistic collapse of stars and galactic nuclei are included in category 7.

The other entries in the first category in Table 1 are computed from equation (8) and our estimates of the other significant contributions to the total mass density, under the assumption that the density parameters sum to unity, that is, space curvature is neglected.