


2.4. Primeval Gravitational Energy
In the  CDM
cosmology the gravitational binding energy of the
present mass distribution has two contributions. The first, which we
term primeval, is a result of the purely gravitational growth of mass
fluctuations out of the small adiabatic departures from a homogeneous
mass distribution present in the initial conditions for the
Friedmann-Lemaître cosmology. The second, to be discussed in the
next subsection, is the result of dissipative settling of baryons that
produced the baryon-dominated luminous parts of the galaxies along with
stars and star remnants. We can find sensible approximations to the
primeval and dissipative components because, as we will discuss, the
characteristic length scales are well separated.
CDM
cosmology the gravitational binding energy of the
present mass distribution has two contributions. The first, which we
term primeval, is a result of the purely gravitational growth of mass
fluctuations out of the small adiabatic departures from a homogeneous
mass distribution present in the initial conditions for the
Friedmann-Lemaître cosmology. The second, to be discussed in the
next subsection, is the result of dissipative settling of baryons that
produced the baryon-dominated luminous parts of the galaxies along with
stars and star remnants. We can find sensible approximations to the
primeval and dissipative components because, as we will discuss, the
characteristic length scales are well separated.
The primeval gravitational energy is defined by imagining a universe with initial conditions identical to ours in all respects except that the baryonic matter in our universe is replaced by an equal mass of CDM in the reference model. At the present world time this reference model contains a clustered distribution of massive halos with gravitational binding energy density that we term the primeval component. 5 This component is estimated as follows.
The Layzer (1963) - Irvine (1961) equation for the evolution of the kinetic and gravitational energies of nonrelativistic matter, such as CDM, that interacts only by gravity is
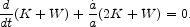 |
(57) |
The kinetic energy per unit mass is
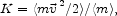 |
(58) |
where  is the
peculiar velocity of a particle with mass
m. The gravitational potential energy per unit mass is
is the
peculiar velocity of a particle with mass
m. The gravitational potential energy per unit mass is
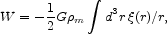 |
(59) |
where
 m is
the mean mass density and
m is
the mean mass density and
 is the reduced mass
autocorrelation function.
is the reduced mass
autocorrelation function.
We can use a simple limiting case of the Layzer-Irvine equation,
because in the  CDM
cosmology the universe has now entered
CDM
cosmology the universe has now entered
 -dominated
expansion, which has caused a significant
suppression of the growth of large-scale departures from homogeneity.
This means that the first term in equation (57) has become
small compared to the second term.
Thus it is a reasonable approximation to take 2K = - W,
the usual virial equilibrium relation. Then the gravitational binding
energy per unit mass is
U = K + W = W / 2, and the cosmic mean
primeval gravitational
binding energy is the product of U with the mean mass density
-dominated
expansion, which has caused a significant
suppression of the growth of large-scale departures from homogeneity.
This means that the first term in equation (57) has become
small compared to the second term.
Thus it is a reasonable approximation to take 2K = - W,
the usual virial equilibrium relation. Then the gravitational binding
energy per unit mass is
U = K + W = W / 2, and the cosmic mean
primeval gravitational
binding energy is the product of U with the mean mass density
 m in
matter (eq. [8]). With the normalization P(k) =
m in
matter (eq. [8]). With the normalization P(k) =
 d3r
d3r
 (r)
ei
(r)
ei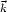 .
.  for the mass fluctuation power spectrum, the expression for the primeval
gravitational binding energy in this approximation is
for the mass fluctuation power spectrum, the expression for the primeval
gravitational binding energy in this approximation is
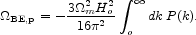 |
(60) |
For a numerical value we use the mass fluctuation power spectrum P(k) in Figure 37 of Tegmark et al. (2004b) at k < 0.1h Mpc-1. At smaller scales the Tegmark et al. spectrum decreases too rapidly with increasing wavenumber k to be a good approximation to the present mass distribution (Davis & Peebles 1983). We approximate the spectrum as
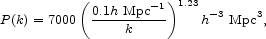 |
(61) |
at k > 0.1h Mpc-1. This is based on the Fourier transform of the pure power law model for the galaxy autocorrelation function (eq. [5]),
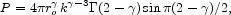 |
(62) |
which gives P = 5200h-3 Mpc3 at k = 0.1h Mpc-1. We choose the somewhat larger normalization in equation (61) to fit the SDSS measurement. The numerical result is
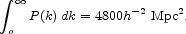 |
(63) |
The integral of the Tegmark et al. (2004b) power spectrum over all wavenumbers is 2700h-2 Mpc, which is 0.55 times the value in equation (63). Our estimate of the integral is based on measurements of the actual power spectrum, not the spectrum that would have obtained if there were no dissipative settling of baryons, but the error is small because the integral is dominated by lengths large compared to the scale of separation of baryons from the dark matter.
Equations (60) and (63) yield the entry in line 4 of Table 1,
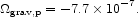 |
(64) |
This is the density parameter of the gravitational binding energy of the present departure from a homogeneous mass distribution, ignoring the effects of the dissipative settling of baryons. It will be useful to note that a measure of the length scale of the gravitational energy is the half-point of the integral in equation (63), at wavenumber k1/2 = 0.27h Mpc-1, or half wavelength
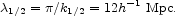 |
(65) |
The kinetic energy per unit mass belonging to equation (64) is
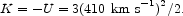 |
(66) |
The velocity in parentheses is the one-dimensional single-particle line-of sight rms peculiar velocity.
The gravitational binding energy is not equal to a sum over the contributions from individual objects, but we can write useful approximations to the decomposition into the three components - the virialized parts of the massive halos of L ~ L* galaxies, the rich clusters, and large-scale clustering - shown in category 4 in the inventory.
Since galaxy rotation curves tend to be close to flat we write the binding energy of the virialized parts of the dark matter halos of the galaxies as
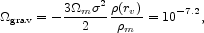 |
(67) |
where  m
is the matter density parameter
(eq. [8]),
m
is the matter density parameter
(eq. [8]),  is the
characteristic velocity dispersion in
equation (10) and the last factor is the virialized mass
fraction (eq. 13). This is about 10% of the total gravitational binding
energy. The dissipative settling that produced the
baryon-dominated luminous parts of the galaxies would have perturbed
the massive halos, but the disturbance to the primeval gravitational
energy is small because the baryon mass fraction is small.
is the
characteristic velocity dispersion in
equation (10) and the last factor is the virialized mass
fraction (eq. 13). This is about 10% of the total gravitational binding
energy. The dissipative settling that produced the
baryon-dominated luminous parts of the galaxies would have perturbed
the massive halos, but the disturbance to the primeval gravitational
energy is small because the baryon mass fraction is small.
Our estimate of the binding energy of the dark halos of the galaxies may
be compared to the density parameter given by equation (60) when the
integral over P(k) is restricted to small scales,
k >  /
rv, where rv is the virial radius in
in equations
(10) and (67). The result, with equation (61) for P(k), is
twice the value in equation (67). The difference is an indication of the
ambiguity of separating gravitational energy into components. For entry
4.1 we adopt the value in equation (67) as the more directly interpretable.
/
rv, where rv is the virial radius in
in equations
(10) and (67). The result, with equation (61) for P(k), is
twice the value in equation (67). The difference is an indication of the
ambiguity of separating gravitational energy into components. For entry
4.1 we adopt the value in equation (67) as the more directly interpretable.
Equation (67) is a reasonable approximation for most of
the mass in galaxy-size dark halos in luminous field galaxies such as
the Milky Way, but in rich clusters the galaxies tend to
share a dark halo that is close to smoothly distributed across the
cluster. Our estimate in entry 4.2 for the primeval gravitational
binding energy belonging to rich clusters follows
equation (67), with
 = 800 km s-1 and
= 800 km s-1 and
 cl from
equation (46).
Rich clusters share about 15% of the total gravitational binding energy.
cl from
equation (46).
Rich clusters share about 15% of the total gravitational binding energy.
Entry 4.3 is the difference between the total in entry 4 and the sum of entries 4.1 and 4.2. The Layzer-Irvine equation indicates that the binding energy is dominated by a length scale (eq. [65]) that is much larger than galaxy virial radii. Consistent with this, entry 4.3 is larger than entry 4.1 for the binding energy of the dark halos of galaxies. The difference is not large, however, because at small scales the integral over the power spectrum converges slowly, as k-0.23.
5 One surely would say that in
this model universe the virialized dark matter halos have gravitational
binding energy. Since there was no energy transfer to some other form, one
might also want to say that this binding energy must have been present
in the initial conditions. Furthermore, one can assign to a linear mass
density fluctuation with contrast
 (t) > 0, and
comoving radius x (physical radius xa(t)), a
gravitational energy per unit mass, W' ~ - G
<
(t) > 0, and
comoving radius x (physical radius xa(t)), a
gravitational energy per unit mass, W' ~ - G
< >
>
 (ax)2,
which is constant in
linear perturbation theory and comparable to the binding energy of the
final virialized halo. Perhaps one can use this as a guide to a
definition of the primeval energy belonging to the density fluctuation,
despite the problem that the mean of W' vanishes, and the fact that
in general relativity theory there is no general definition of the
global energy density of a statistically homogeneous system. We have
not been able to find a useful approach along these lines. We
might add that if our universe had been Einstein-de Sitter then we
would have defined the primeval energy density by a numerical solution
of equation (57).
Back.
(ax)2,
which is constant in
linear perturbation theory and comparable to the binding energy of the
final virialized halo. Perhaps one can use this as a guide to a
definition of the primeval energy belonging to the density fluctuation,
despite the problem that the mean of W' vanishes, and the fact that
in general relativity theory there is no general definition of the
global energy density of a statistically homogeneous system. We have
not been able to find a useful approach along these lines. We
might add that if our universe had been Einstein-de Sitter then we
would have defined the primeval energy density by a numerical solution
of equation (57).
Back.