2.3. The Baryon Rest Mass Budget

The entries in this category refer to the baryon rest mass: one must add the negative binding energies to get the present mass density in baryons. The binding energies are small and the distinction purely formal at the accuracy we can hope for in cosmology, of course, with the conceivable exception of the baryons sequestered in black holes.

We begin with the best-characterized components, the stars, star remnants, and planets. We then consider the diffuse components, and conclude this subsection with discussions of the baryons in groups and the intergalactic medium and the lost baryons in black holes.

2.3.1. Stars

This is an update of the analysis in FHP. Following the same methods, we estimate the baryon mass in stars from the galaxy luminosity density and the stellar mass-to-light ratio, M_stars / L, along with a stellar initial mass function (the IMF) that allows us to estimate the mass fractions in various forms of stars and star remnants.

The integrated luminosity densities from the SDSS broad-band galaxy luminosity function are (Yasuda et al. in preparation)

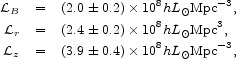(21)

where _B is inferred from the densities in other color bands.

Kauffmann et al. (2003) present an extensive analysis of the stellar mass-to-light ratio based on ugriz photometry for 10⁵ SDSS galaxies and a population synthesis model (Bruzual & Charlot 2003) that is meant to take account of the stellar metallicities and the star formation histories. Their estimate of the stellar mass-to-light ratio is M_stars / L_z 1.85 for luminous galaxies, with magnitudes M_z < M_z^* - 0.8, and it decreases gradually to M_stars / L_z 0.65 for fainter galaxies with M_z M_z^* + 3. Our estimate of the resulting luminosity-function-weighted mean is

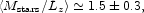(22)

for the IMF Kauffmann et al. used. Equation (22) represents the present mass in stars and stellar remnants, and it excludes the mass shed by evolving stars and returned to diffuse components.

The estimate of M_stars / L assumes a universal IMF, which is not thought to seriously violate the observational constraints. The IMF is not tightly constrained, and it is particularly uncertain at the subsollar masses that make little contribution to the light but can make a considerable contribution to the mass. We consider two continuous broken power law models, of the form

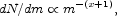(23)

where, in the first model,

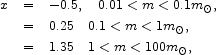(24)

and, in the second model,

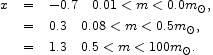(25)

The first line in the first model is from Burgasser et al. (2003), and the second line is from Reid, Gizis, & Hawley (2002). The third line, for m > 1 m, is the standard Salpeter (1955) IMF. The second model is from Kroupa (2001). For our model IMF we take the Salpeter index for m 1 m. It is known that the Salpeter-like slope gives the correct UBV colour and H equivalent widths for normal galaxies (Kennicutt 1983). For the subsolar IMF, we take the geometric mean of the above two models, and we take the difference as an indication of the error (± 18%).

The stellar mass-to-light ratio in equation (22) assumes the IMF in equation (25). With our adopted IMF the stellar mass-to-light ratio is 1.18 times the number in equation (22). ⁴ Thus we get our fiducial estimate,

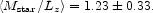(26)

This translates to M / L_B 2.4, or 0.7 times that used in FHP, which employed the subsolar mass IMF of Gould, Bahcall & Flynn (1996). In the Salpeter IMF, with x = 1.35 cut off at 0.1 m, the mass-to-light ratio is 1.48 times our adopted value. The Kennicutt (1983) IMF results in 0.81 times equation (26).

The IMF at substellar masses, m < 0.08 m, is more uncertain, but recent observations of T dwarfs indicate x < 0 (e.g., Burgasser et al. 2003). In the two IMF models quoted above the substellar mass is 6 to 9% of the mass integral for 0.08 < m < 1 m. We adopt 8% and assign an error of 50%.

We estimate the mass density locked in stars, including those in dead stars, to be _stars = 0.0025 ± 0.0007. A comparable estimate is derived from b_J, J, K_s multicolour photometry of 2MASS combined with 2dF data by Cole et al. (2001), _stars = 0.0029 ± 0.0004 with the IMF we have adopted. For the energy inventory we take the mean of our present number and that of Cole et al.:

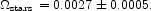(27)

This means that the stars contain 6.0 ± 1.3% of the total baryons. The FHP estimate is _stars = 0.0019 - 0.0057. Equation (27) also is consistent within the errors with the more recent estimates by Salucci & Persic (1999), Kochanek et al. (2001), and Glazebrook et al. (2003), and with Shull's (2003) baryon inventory.

We attempt to partition the stars into their species. Our estimates of the mass fraction in stars on the main sequence (MS), and the mass fractions in stellar remnants, including white dwarfs (WD), neutron stars (NS) and stellar mass black holes (BH), are shown in Table 2. Stars on the MS are represented by the present-day mass function (PDMF), which for 1 < m < 100 m is constructed by multiplying the IMF by m^-2.5 to account for the lifetime of massive main sequence stars; for m < 1 m the PDMF is the same as the IMF.

Table 2. Star mass fractions

initial mass range	fate	remnant a	mass fraction	mass consumed b
0.01 < m < 0.08	SS	...	0.052	0.052
0.08 < m < 100 c	MS	...	0.769	0.769
1 < m < 8	WD	0.62	0.135	0.463
8 < m < 25	NS	1.35	0.019	0.186
25 < m < 100	BH	7.5	0.025	0.146
sum			1.0	1.616
a Mass in units of Solar masses
b The gas consumed to make unit mass of stars now present.
c For the mass range 1 < m < 100 m those stars burning today are counted.

As indicated in the third line of Table 2, we take the average mass of a white dwarf to be <m> = 0.62 m, for consistency with the model we describe in section 2.5.2 (eq. [70]). This is close to the value from recent observations, 0.604 m (Bergeron & Holberg, in preparation; Bergeron private communication). We assume all stars with initial masses in the range 1 < m < 8 m end up as white dwarfs with the adopted average mass, and the rest of the mass returns to the interstellar medium. With our adopted IMF this model predicts that the ratio of masses in white dwarfs to main sequence stars is (WD) / (MS) = 0.176. This can be compared to the observations. The 2dF survey (Vennes et al. 2002), with the use of our mean mass 0.62 m, yields a measure of the mass density of DA white dwarfs, (DA-WD, local) = (4.2 ± 2.3) × 10^-3 m pc^-3. This is multiplied by 1.3 to account for DB, DQ and DZ white dwarfs (Harris et al. 2003), to give the total white dwarf mass density (WD, local) = (5.5 ± 3.0) × 10^-3 m pc^-3. This divided by the local density of main sequence stars, (MS, local) = 0.031 ± 0.002 m pc^-3, from Reid, Gizis, & Hawley (2002), gives (WD) / (MS) = 0.18 ± 0.10, which agrees with our model prediction, albeit with a large uncertainty.

We assume all stars in the initial mass range

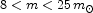(28)

end up as neutron stars with mass 1.35 m (Nice, Splaver, & Stairs 2003; Thorsett & Chakrabarty 1999), and the rest of the star mass is recycled. Estimates of the lower critical mass for stellar core collapse vary from 6 to 10 m (Reimers & Koester 1982; Nomoto 1984; Chiosi, Bertelli, & Bressan 1992). The upper critical mass for the formation of a neutron star is more uncertain; our choice in equation (28) is taken from Heger et al. (2003). We assume all stars with main sequence mass above the limit in equation (28) end up as stellar black hole remnants with mass m = 7.5 m, with the rest of the mass recycled. This again follows Heger et al. The remnant mass is quite uncertain, and Heger et al. also indicate that some stars with masses above the range in equation (28) may produce neutron stars.

The last column in Table 2 is the total amount of mass that has gone into stars, including what is later shed, normalised to the mass in column (4). According to these estimates, 1.6 times the mass in observed stars was used (and reused) in star formation.

Entries 3.3 to 3.8 in Table 1 are based on the partition of _stars among main sequence stars and star remnants in the fourth column of Table 2, with the FHP partition between the two galaxy population types in the proportion

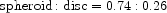(29)

of mass in ellipticals plus bulges of spirals to the mass in disks plus irregulars. The objects in the mass range 0.01 < m < 0.08 m are classified as `brown dwarfs', or substellar objects (SS), in Tables 1 and 2.

2.3.2. Consistency with the Star Formation Rate

We can compare our estimate of the mass in stars to the mass integrated over the star formation rate density (the SFR) from high redshift to the present. The H luminosity density at zero redshift measured from an SDSS nearby galaxy sample is (H ) = 10^{39.310.11_-0.08} h erg s^-1 Mpc^-3 (Nakamura et al. 2004). This agrees with the earlier value obtained by Gallego et al. (1995). Within the star formation models Glazebrook et al. (1999) explored, 1 m yr^-1 of star formation produces H luminosity L = (2.00^+0.92_-0.24) × 10⁴¹ erg s^-1 for our adopted IMF. The ratio of (H ) to L is an estimate of the present-day SFR,

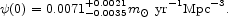(30)

The evolution of the SFR at z 1 is now observationally well determined (Lilly et al. 1996; Heavens et al. 2004; see Glazebrook et al. 1999 for a summary of the measurements up to that time), and may be approximated as

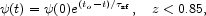(31)

where

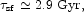(32)

and t_o - t is the time measured back from the present in the CDM cosmology (Fukugita & Kawasaki 2003; see also Glazebrook et al. 1999). The situation at higher redshift is still controversial (Madau et al. 1996; Steidel et al. 1999). We shall suppose that the SFR is constant from z = 0.85 back to the start of star formation at redshift z_f, at the value

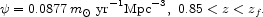(33)

In this model the integrated star formation is

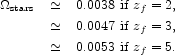(34)

There is a significant downward uncertainty, _stars ~ - 0.0025, arising from the uncertainty in the star formation rate (eq. [30]). Equation (27) and Table 2 indicate that the mass processed into stars, including what was later shed, is = 0.0027 × 1.62 = 0.0044. This is consistent with the cumulative star formation in equation (34). There would be a problem with the numbers if there were reason to believe that the SFR continued to increase with increasing redshift well beyond z = 1. A constant or declining SFR at z > 1 is well accommodated with our estimates for the baryon budget and current ideas about the star formation history at high redshift.

The star formation history determines the average reciprocal redshift factor (as in eq. [100]) for the effect of redshift on the integrated comoving energy density of electromagnetic radiation (and other forms of relativistic mass) generated by stars. In our model for the SFR the correction factor is

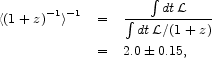(35)

where (t) is the bolometric luminosity density per comoving volume, which we are assuming is proportional to the star formation rate density. The numerical value assumes the redshift cutoff is in the range z_f = 2 to 5. For the purpose of comparison of the accumulation of stellar products to the present rate of production, another useful quantity represents the integrated comoving density of energy radiated in terms of the effective time span normalised by the present-day luminosity density,

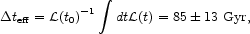(36)

The value assume the range of models for the star formation history in equation (34).

We can compare the rate of stellar core collapse in our model to observations of the supernova rate. (See Fukugita & Kawasaki 2003 and Madau, della Valle & Panagia 1998 for similar analyses). The present SFR in equation (30) and the critical minimum mass 8 m in equation (28) imply that the present rate of formation of neutron stars and stellar black holes is expected to be

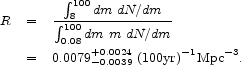(37)

Our estimate of the observed supernova rate is

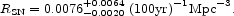(38)

This is the geometrical mean of the rates from three surveys for Type II and Type Ib/c supernovae, 0.037, 0.018 and 0.017, in units of h³(100 yr)^-1 Mpc^-3 (Tammann, Löffler & Schröder 1994; Cappellaro et al. 1997; van den Bergh & McClure 1994; see also Cappellaro, Evans & Turatto 1999). We conclude that, if most stars with initial masses greater than about 8 m produced Type II and Ib/c supernovae, then our model for the star formation history would pass this consistency check.

We remark that in our model the comoving number density of supernovae of types II and Ib/c integrated back to the start of star formation is

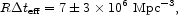(39)

where the effective time span is given in equation (36).

2.3.3. Planets and Condensed Matter

The mass in planets that are gravitationally bound to stars must be small, but it is of particular interest to us as residents of a planet. Marcy (private communication; see also Marcy & Butler 2000) finds that about 6.5% of nearby FGKM stars have detected Jovian-like planets, and that an extrapolation to planets at larger orbital radii might be expected to roughly double this number. In our model for the PDMF the ratio of the number density of stars in the mass range 0.08 to 1.6 m to the mass density in stars is n / = 2.1 m^-1. The product of this quantity with the mass density in stars (eq. [27]), the fraction 0.13, and the ratio of the mass of Jupiter to the Solar mass is

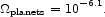(40)

Marcy indicates that stars with lower metallicity have fewer planets, but that may not introduce a serious error because there are fewer low metallicity stars. There is a population of interstellar planets that have escaped from stars that have shed considerable mass. The mass fraction in escaped planets might be expected to be comparable to the mass fraction of stars that have exploded, and hence subdominant to equation (40). The large uncertainty is whether the stellar neighborhood a fair sample. This leads us to enter the order of magnitude in Table 1.

We consider separately the mass in objects small enough to be held together by molecular binding energy rather than gravity. The dominant amount of the former is interstellar dust. It is known (Draine 2003) that 90% of silicon atoms in interstellar matter are condensed into grains, probably dominantly in the forms of enstatite (MgSiO₃) and forsterite (Mg₂SiO₄) with the former likely three to four times more abundant (Molster et al. 2002). This means the mass in this form is Z(silicates) / Z = 0.17 times the mass in heavy elements. Draine (2003) suspects that the dominant contribution to the carbonaceous material is in the form of polycyclic aromatic hydrocarbon with the inferred abundance C/H = 6 × 10^-5. Adding this to the silicates, we find that the mass fraction becomes Z(dust) / Z = 0.20. The formation of dust with iron or other forms of carbonates could increase this number. Entry 3.12 is the product of the density parameter in cool gas (entries 3.9 plus 3.10) with the mean metallicity discussed below (and displayed as eq. [86]) and the 20 percent heavy element mass fraction in dust. Our estimate, which assumes that what we know about the Milky Way applies to other galaxies, is crude, but it seems likely that the mass in dust exceeds the mass in planets.

There are larger objects in which molecular binding is important. The gravitational binding energy of a roughly spherical object with mass m and radius r is ~ Gm² / r, and the molecular binding energy is roughly 1 eV per atom. The molecular binding energy is larger than the gravitational energy when

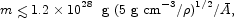(41)

where the mass density is and the mean atomic weight is 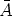. For silicates, this bound is m = 8 × 10²⁶ g. That is, gravitational binding energy dominates in the Earth and molecular binding energy dominates in the Moon and asteroids. Trujillo, Jewitt, & Luu (2001) estimate that the mass in the Kuiper Belt objects is about a tenth of an Earth mass, or 10^-6.5 m. A comparable mass is in the moons in the Solar system. If this mass fraction were common to all stars the density parameter in these objects would be

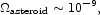(42)

a small fraction of the mass in dust.

2.3.4. Neutral Gas

The recent blind HI surveys are a significant advance over the data used by FHP to estimate the mass density in neutral atomic gas. The largest survey, HIPASS, with 1000 galaxies (Zwaan et al. 2003), gives

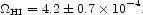(43)

The increase over the value quoted in FHP (1.5 times the upper end value of FHP) illustrates the advantage of blind surveys over observations of programmed galaxies. The molecular hydrogen abundance from the CO survey of Keres, Yun & Young (2003) is

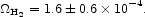(44)

The sum of these two values is multiplied by 1.38 to accommodate helium.

We place in entry 3.9 the atomic hydrogen and the helium abundance belonging to atomic and molecular hydrogen. Entry 3.10 is the molecular hydrogen component. The mass in this neutral gas is 1.7± 0.4% of the total baryon mass.

2.3.5. Intracluster Plasma

The estimate of the plasma mass in rich clusters of galaxies depends on a convention for the cluster radii and masses. We use the mass M₂₀₀ contained by the nominal virial radius, r₂₀₀. This definition is more faithful to a physical definition of the part of a cluster that is close to dynamical equilibrium, and it also traces the X-ray radius which is the definition of our hot gas. In the limiting isothermal sphere model the relation to the mass within the Abell radius r_A = 1.5h^-1 Mpc is

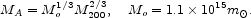(45)

This agrees with the estimates of the two masses given by Reiprich & Böhringer (2002), Table 4. We adopt the Reiprich & Böhringer cluster mass density parameter,

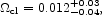(46)

for the cluster mass limit

(47)

The Bahcall & Cen (1993) Abell mass function is consistent with the Reiprich & Böhringer estimate. We caution that the Bahcall et al. (2003) SDSS mass function is about half what we adopt, perhaps because SDSS samples a subset of the clusters. Note also that the integral over the cluster mass within the Abell radius gives a substantially larger value for _cl because M_A > M_o at the masses M 10¹⁴ m that dominate the integral for a given mass function.

The abundance of hot baryons in clusters is obtained from the expression

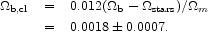(48)

The change from the value in FHP is mainly due to the definition of the cluster mass, as also noted by Reiprich & Böhringer.

2.3.6. Massive Black holes

We follow the standard idea that the massive objects in the centers of galaxies are black holes that formed by the accretion of baryons. Baryons entering black holes are said to lose their identity, but for our accounting it is appropriate to consider them to be sequestered baryons.

We define the characteristic efficiency factor _n for black hole formation (where the subscript is meant to distinguish the massive black holes in the centers of galaxies from stellar mass black holes) by the black hole mass produced out of an initial diffuse baryon mass m_b,

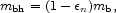(49)

where the energy released in electromagnetic radiation, neutrinos, and kinetic energy is

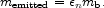(50)

The baryon mass sequestered in massive black holes, m_b = m_bh / (1 - _n), could be substantial if _n were close to unity. However, if an appreciable part of the binding energy were released as electromagnetic radiation then the bounds on the radiation background (in category 7) and those of the CMBR distortion (eq. [14]) would require that the energy was released at very high redshift, kT > 10⁷ K. It seems much more likely that _n is small, as is assumed in entry 3.13. The efficiency factor _s typical of stellar mass black holes does not appear in entry 3.7, because this estimate is based on an analysis of the progenitor star masses. The estimate of the mean mass density in massive black holes that is used for entry 3.13 is discussed in Section 2.5.3.

2.3.7. Intergalactic Plasma

Entry 3.1, for the baryon mass outside galaxies and clusters of galaxies, is the difference between our adopted value of the baryon density parameter (eq. [16]) and the sum of all the other entries in category 3. Within standard pictures of structure formation this component could not be in a compact form such as planets, but rather must be a plasma, diffuse enough to be ionized by the intergalactic radiation or else shocked to a temperature high enough for collisional ionization, but not dense and hot enough to be a detectable X-ray source outside clusters and hot groups of galaxies.

In our baryon budget 90% of the baryons are in this intergalactic plasma. It is observed in several states. Quasar absorption lines show matter in low and high atomic ionization states in the halos of L ~ L_* galaxies, extending to radii ~ 200 kpc (Chen et al. 2001 and references therein). Absorption lines of HI and MgII reveal low surface density photoionized plasma at kinetic temperature T ~ 10⁴ K, which can be well away from L ~ L_* galaxies, as discussed by Churchill, Vogt, & Charlton (2003), and Penton, Stocke & Shull (2004). The latter authors estimate that 30% of the baryons are in this state. Absorption lines of O VI around galaxies and groups of galaxies (Tripp, Savage & Jenkins 2000; Sembach et al. 2003; Shull, Tumlinson, & Giroux 2003; Richter et al. 2003), reveal matter that may be excited by photoionization by the X ray background radiation and by collisions in plasma at the kinetic temperature T ~ 10⁶ K characteristic of the motion of matter around galaxies (Cen et al. 2001). Improvements in the constraints on the amount of matter in these various states of intergalactic baryons will be followed with interest.

For the inventory we adopt the measure of the concentration of dark matter around galaxies in equation (13), and the argument discussed in Section 2.3.8 that the baryons are distributed like the dark matter on scales comparable to the virial radii of galaxies. The resulting division into the mass in baryons near the virial radii of normal galaxies outside clusters (entry 3.1a), and the mass well away from galaxies and compact groups and clusters of galaxies (entry 3.1b), is presented as sub-components, because the sum is much better constrained than the individual values.

2.3.8. Baryon Cooling

We comment here on a simple picture for the cooling and settling of baryons onto galaxies. The sum of the baryon mass densities belonging to galaxies, in entries 3.3 to 3.13, is _{b, g} = 0.0035. This is 8% of the total baryon mass. Suppose _{b, g} consists of all baryons gathered from radius r_g around L ~ L_* galaxies, and we can neglect the addition of baryons by settling from further out and the loss by galactic winds. That is, we are supposing that at r > r_g the ratio of the baryon density to the dark matter density is the cosmic mean value, and that the baryons closer in have collapsed onto the galaxies. In this picture the characteristic radius of assembly of the baryons satisfies

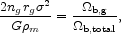(51)

in the limiting isothermal sphere approximation (eq. [9]).

In equation (51) n_g is a measure of the number density of luminous galaxies. We record here our choices for this quantity and related parameters that are used elsewhere. We take

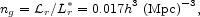(52)

where _r is the luminosity density (eq. [21]). The characteristic galaxy luminosity,

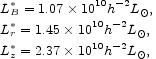(53)

is the luminosity parameter in the Schechter function, with the power law index _B = - 1.1, _r = - 1.13, and _z = - 1.14. We refer some estimates of energy densities to what is known about the Milky Way, for which we need the effective number density of Milky Way galaxies. In the B band the Milky Way luminosity is L_MW = 1.7 L_B^* (based on the Sakai et al. 2000 calibration of the B-band Tully-Fisher relation, with W₂₀ = 2 × 220 km s^-1 for the Milky Way), and the effective number density is

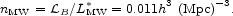(54)

Almost the same density follows when referred to the r-band.

With the characteristic velocity dispersion in equation (10) and the characteristic galaxy number density in equation (52) the baryon accretion radius defined by equation (51) is

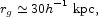(55)

at density contrast 1.3 × 10⁴ and plasma density n_gas(r_g) ~ 0.007 h³ cm^-3. If plasma at this radius were supported by pressure at the one-dimensional velocity dispersion 160 km s^-1 in equation (10) the temperature would be T 2 × 10⁶ K. At this density and temperature the thermal bremsstrahlung cooling time would be short enough, ~ 4 × 10⁹ yr, that stars would have formed and disks matured at z ~ 1.

We have lower bounds on the cooling radius from the observation that the neutral atomic hydrogen density around L_* galaxies reaches N_HI = 1.8 × 10²⁰ cm^-2 at the effective radius ~ 20 h^-1 kpc (Bosma 1981), and Mg II absorption lines are observed at radius ~ 40 h^-1 kpc (Steidel, Dickinson & Persson 1994). For the Milky Way the distribution of RR Lyr stars cuts off sharply at 50 kpc (Ivezic et al. 2000). The cooling radius must be larger than these indicators of relatively cool matter. Equation (55) is not inconsistent with this condition. Though the history of baryon accretion by galaxies undoubtedly is complex, we can imagine, as a first approximation, that a substantial fraction of the baryons now concentrated in galaxies are there because they were able to cool and settle from an initial distribution similar to that of the dark matter.

The relative distributions of baryons and dark matter at distances much larger than r_g from galaxies might not be greatly disturbed from the primeval condition. If so, then the product of the baryon density parameter with the virialized dark matter mass fraction in equation (13) is an estimate of the baryon mass that resides within the virial radii of normal galaxies, and the remainder,

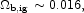(56)

which is presented as entry 3.1b, would be located outside galaxies and remain less than fully documented.

⁴ The IMF are normalised so that the mass integrals between 0.9 and 2.0 m are equal. The result is virtually identical with those with the two IMFs normalised at 1m. Back.