2.9. Cosmic Rays and Magnetic Fields

This estimate is based on the rate of production of cosmic rays in the Milky Way galaxy. We start from the radio structure. In their analysis of the Haslam et al. (1982) measurements, Beuermann, Kanbach, & Berkhuijsen (1985) write the radio luminosity distribution at 408 MHz as the sum of thin and thick components. We model each distribution, in an approximation to their results, as

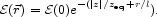(122)

In the thick component the scale heights in the disk and perpendicular to the disk are

(123)

scaled to Solar galactocentric distance 8 kpc. The total luminosity in the thin component in this model may be neglected, but the thin component is a significant contribution to the local luminosity density, : the local thick component fraction is (thick) / = 0.55. We assume the energy density in cosmic rays is proportional to the luminosity density at 408 MHz. A more detailed model would take account of the spatial variation of the magnetic field strength, but that will be left for future studies. We normalize to the local energy density, 1.8 eV cm^-3, in relativistic cosmic rays (Webber 1998). In these approximations the energy of cosmic rays in the galaxy is 10^56.1 erg. We take the cosmic ray mean life in the galaxy to be 2 × 10⁷ yr (Garcia-Munoz, Mason & Simpson 1977; Yanasak et al. 2001). The ratio is a measure of the cosmic ray luminosity, 10^41.3 erg s^-1. If the acceleration of cosmic rays is mainly due to shocks of Type II and Ibc supernovae, ¹⁰ following the conventional wisdom (Ginzburg & Syrovatskii 1964), the cosmic ray luminosity is proportional to the star formation rate. Thus the product of this luminosity with the effective time (eq. 36) and the redshift factor (eq. [35]) is an estimate of the contribution of the Milky Way to the present energy in cosmic rays. The product with the effective number density of Milky Way galaxies (eq. [54]) is our estimate of the present energy density in cosmic rays from normal galaxies,

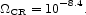(124)

The radio luminosity of the Milky Way offers a check of this calculation. The Beuermann et al. (1985) luminosity of the Milky Way, 5.5 × 10²¹ W Hz^-1 at = 408 GHz, scaled to 1.4 GHz by the ^-0.8 power law (neglecting the small thermal bremsstrahlung component), and multiplied by the effective number density of Milky Way galaxies (eq. [54]), is _g = 8 × 10¹⁸ W Hz^-1 Mpc^-3, about half the Condon et al. (2002) measurement of the mean luminosity density of the galaxies (eq. [110]). That is, the evidence is that the Milky Way gives a reasonably good measure of the synchrotron luminosity density of the galaxies, and hence of the cosmic ray luminosities of galaxies. This is not a very direct check of the assumed universality of the cosmic ray lifetime in the source galaxy, of course.

A similar energy may be present in the magnetic field. If the leakage of cosmic rays approximated a fluid flow, magnetic field would leak into intergalactic space with the cosmic rays. Application of equipartition to equation (124) would suggest that the cosmic rms magnetic field strength is

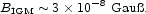(125)

If the estimate of the local ratio of the cosmic ray to magnetic field energy density, 8:1 (the magnetic field corresponding to 3 µGauß), applied to the intergalactic medium, it would lower equation (125) by a factor of three.

The product of the integrated production of supernovae (eq. [39]; the contribution from Type Ia supernovae is less than 10% of that from Type II and Ib/c) with the characteristic kinetic energy, E_KE 1.6 × 10⁵¹ erg, released in a supernova (Arnett 1996), is an estimate of the integrated kinetic energy production per comoving volume,

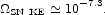(126)

If the fraction _cr of this energy were placed in relativistic intergalactic particles, the present energy density in this component, taking account of the redshift factor, would be

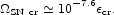(127)

This is consistent with the picture that a fraction _cr ~ 0.2 of the kinetic energy liberated by supernovae has been deposited in intergalactic cosmic rays (eq. [124]).

Cosmic rays might gain energy from the streaming motions of magnetized warm plasma in the vicinity of galaxies (Loeb & Waxman 2000). However, since the energy available in the plasma (eq. [128] below) is less than the energy liberated by supernovae (eq. [124]), this process is not likely to substantially affect the energy in cosmic rays.

What is the AGN contribution to the cosmic ray energy density? Though AGNs are not major sources at optical wavelengths, their contribution to the radio background is comparable to that of the larger number of normal galaxies (eq. [110). This is an indication of the importance of AGNs for high energy processes. If the cosmic ray energy production by AGNs were proportional to the production of synchrotron radio emission, the energy of cosmic rays from AGN's (including radio elliptical galaxies) would be comparable to, or even larger than, that from the normal galaxies, and our estimate in eq. (124) would have to be doubled. It is important also that AGNs may accelerate cosmic rays to higher energies than do normal galaxies.

We use equation (124) in the inventory. The lower error flag for the entry in Table 1 is based on the evidence that the Milky Way gives a fair measure of galaxy radio luminosities. The larger upper error flag reflects the possibly significant roles of the intergalactic magnetic field and AGNs.

¹⁰ No type Ia supernova remnants are known to give strong radio sources (Weiler et al. 1986). This implies that Type Ia supernovae contribute little to the acceleration of cosmic rays. Back.