2.8. Products of Stellar Evolution

It is in principle straightforward to compute the integrated outputs of stellar evolution - energy, neutrinos, helium, and heavy elements - given models for the IMF, the star formation history, and stellar evolution. Since the details of the results of stellar evolution computations are not easily assembled, we use approximate estimates by procedures similar to those developed in Section 2.3.1 and 2.3.2 for the stellar population and its evolution. The results add to the checks of consistency of our estimates of the stellar production of helium and heavy elements and the resulting total energy release, and are used to estimate the inventory entries for the neutrino cosmic energy density.

2.8.1. Stellar Evolution

All stars with masses m < 1 m are still on the main sequence. We assume that on average 5% of the hydrogen in these subsolar stars has been consumed, with energy production efficiency 0.0071. Most of the stars with masses m > 1 m have already undergone full evolution and left compact remnants, while the fraction ~ (m / m)^-2.5 is still on the main sequence. We assume that in the latter stars on average 5% of the hydrogen has been consumed, as for subsolar stars. For the evolved stars we do not attempt to follow the details of nuclear burning and mass loss. Instead, we adopt estimates of the nuclear fuel consumed or mass lost in a few discrete stages of evolution, in a similar fashion to the approach used in Section 2.3.1 to tally stellar remnants.

When the amount of hydrogen consumed in stellar burning is 10% of the mass of a star it leaves the main sequence. In the model in Section 2.3.1, stars with masses in the range 1 < m < 8m eventually produce white dwarfs that mainly consist of a carbon-oxygen core. In standard stellar evolution models, hydrogen burning extends outward to a shell after core hydrogen exhaustion, and helium burning similarly continues in a shell after core helium exhaustion. That leaves a CO core with the mass given by equation (69). The helium layer outside the CO core is thin for m < 2.2 m, for which helium ignition takes place as a flash, but in stars with masses m > 2.2 m a significant amount of helium is produced outside the core, transported by convection to the envelope, and liberated. A 5 m star liberates 0.4 m of helium and produces a core with mass 0.85 m (e.g., Kippenhahn, Thomas & Weigert 1965). We model the helium production as a function of the initial star mass m as

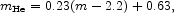(114)

in solar mass units. The energy production in hydrogen shell burning is the product of this mass with the post-stellar hydrogen mass fraction, 0.71 (eq. [85]), and the efficiency factor, 0.0071. Helium burning in the core produces energy with efficiency factor 0.0010.

For stars with masses m > 8m we adopt the helium yield from Table 14.6 of Arnett (1996), ⁹ which we parametrise as

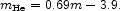(115)

This connects to equation (114) at 8.7 m. We take the CO core mass as a function of the initial stellar mass from Arnett (1996):

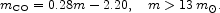(116)

We use an interpolation of eqs. [69] and [116] for stellar masses between 8 and 13m. The energy release is 0.0071 × 0.71 per unit mass for He production, and 0.0014 for CO core formation and the further heavy element production.

The energy output obtained by integration over the IMF and PDMF is

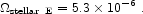(117)

The partition into each phase of stellar evolution and stellar mass range is given in Table 5, where the numbers are normalised to equation (117). About 60% of the energy is produced in the evolved stages.

Table 5. Stellar energy production ^a

stage of stellar evolution	0.08 - 1 m	1 - 8 m	8 - 100 m	sum
main sequence	0.11	0.20	0.12	0.43
H shell burning		0.18	0.29	0.48
core evolution		0.05	0.04	0.09
sum	0.11	0.43	0.46	1.00
a Normalised to = 5.3 × 10-6.

The estimate of the total energy generation in equation (117) is in satisfactory agreement with our estimate of the nuclear binding energy, _BE = 5.7 × 10^-6 (eq. [97]), and the energy production required to produce our estimate of the present radiation energy density, ₊ = (5.1± 1.5) × 10^-6 (eq. [106] corrected for neutrino emission, as discussed in Section 2.8.2). That is, our models for stellar formation and evolution are consistent with our estimates of the accumulation of heavy elements and the stellar background radiation.

In our models for stellar formation and evolution the mass of helium that has been liberated to interstellar space is

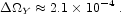(118)

This may be compared to our estimate from the production of heavy elements and the associated production of helium, _Y = 1.7± 1 × 10^-4 (eq. [94]). The heavy element production is calculated in a similar way. The current wisdom is that a neutron star or black hole is left at the end of the evolution of a star with mass m > 8 m, and the rest of the mass is returned to the interstellar medium. On subtracting the remnant mass (indicated in Table 2) from the total heavy element mass produced, we find that in our model the heavy element production is

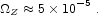(119)

The more direct estimate in equation (92) is _Z' 8 × 10^-5.

We suspect the checks on helium and heavy element production in equations (118) and (119) are as successful as could be expected. In particular, equation (116) for the CO core mass is not tightly constrained. One must consider also the possibility that some supernovae do not produce compact remnants, as is suggested by the cases of Cas A and SN1987A. The maximum heavy element production when there are no remnant neutron stars or black holes is three times the value in equation (119), and larger than _Z' (eq. [92]).

2.8.2. Neutrinos from Stellar Evolution

We need the fraction f of the energy released as neutrinos by the various processes of nuclear burning. In stars with masses m < 1.4 m, energy generation in hydrogen burning is dominated by the slow reaction p + p d + e⁺ + _e. This produces neutrinos with mean energy 0.265 MeV, which amounts to f = 0.020 times the energy generated in helium synthesis. In a Solar mass star electron capture of ⁷Be adds 0.005 to the fraction f. The neutrino energy emission fraction is larger in higher mass (m > 1.4 m) main-sequence stars in which the CNO cycle dominates. In this process, the neutrinos produced in the ⁺ decays of ¹³N and ¹⁵O carry away the energy fraction f = 0.064. The fraction increases to 0.075 for m 2m, when the subchain ¹⁵N-¹⁶O-¹⁷F-¹⁷O-¹⁴N starts dominating and neutrinos are produced by the beta decay of ¹⁷F. This sidechain also dominates during shell burning.

The integral of these factors over the stellar IMF normalised to the present-day mass density _star = 0.0027 (eq. [27]), together with our prescription for energy generation in Table 5, yields the neutrino energy production,

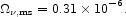(120)

The temperatures and densities that are reached up to carbon burning are low enough that there is negligible neutrino energy loss from neutrino pair production processes.

The temperatures after carbon burning are high enough that the neutrino energy loss dominates, that is, f 1 (Weaver et al. 1978). Thus we may take it that the extra binding energy (BE) of the elements heavier than ²⁰Ne with respect to the binding energy of carbon represents the neutrino energy emitted in the late stages of stellar evolution. On multiplying the heavy element mass (the sum of entries 1, 2 and 4 to 9 in Table 3) by (Z_i / Z) (BE)_i (where <(BE)> = 0.0004 for the solar mix of element abundances, and Z_i / Z = 0.35 is from Grevesse & Sauval (2000), we obtain

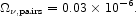(121)

The sum of equations (120) and (121) is 7% of the total energy production (eq. [117]). The present energy density of the stellar neutrinos, in entry 8.1 in Table 1, is the product of this sum with the redshift loss factor ~ 0.5 (eq. [35]).

2.8.3. White Dwarfs and Neutron Stars

Most of the gravitational energy liberated in white dwarf formation goes to neutrinos, and in the latest stage to X-rays. Since the latter is small the contribution to the neutrino energy density (entry 8.2 in the inventory) is the product of the gravitational binding energy in entry 5.3 with the redshift factor.

More than 99% of the energy released in core collapse also is carried away by neutrinos. Thus we similarly obtain entry 8.3 by multiplying entry 5.4 by the redshift factor.

⁹ This helium yield is significantly larger than Arnett's helium core mass, m_He = 0.43m - 2.46. Back.