D. The pairwise velocity dispersion

The pairwise velocity dispersion of galaxies is a measure of the temperature of the "gas" of galaxies. By energy conservation, the kinetic energy of this gas has to be balanced by its gravitational energy, which depends mainly on the mean mass density of the Universe. Thus, measuring the pairwise velocity dispersion gives us a handle on the density. This is, however, more easily said than done since we measure only the radial component of the velocity, and that is biased by larger density inhomogeneities than a linear theory can handle.

The following short argument shows how the velocity dispersion relates to the fluctuations in the density field. The non-Hubble component of a galaxy velocity through the Universe, (its peculiar velocity), is due to the acceleration caused by clumps in the matter distribution. This is easy to estimate during the phase of linear evolution of cosmic structure since linear perturbation theory applies.

A particle that has experienced a peculiar acceleration g_p for a time t would have acquired a peculiar velocity v_p ~ g_p t. If this acceleration is due to a mass fluctuation M at distance r, we have

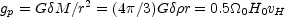(28)

which leads to

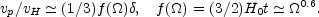(29)

For a more general approximation including the cosmological constant see Lahav et al. (1991). As one can see the ratio of the peculiar to Hubble velocity is the quantity that gives a direct measure of the amplitude of primordial density fluctuations on a given scale for a given value of . If we have a scaling law for the density fluctuations we should also see a scaling law in the peculiar velocity field.

A more detailed calculation, still using linear theory, gives a direct relation between the rms amplitude of the peculiar velocity and the power spectrum of primordial density fluctuations (Strauss and Willick, 1995):

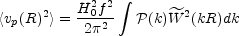(30)

where 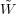(kR) is the Fourier transform of a spherical window function of radius R, W(R). This equation also works quite well for rather high , well beyond the linear regime. The main problem then becomes dealing with the redshift distortion of the observed velocity field.

This equation, however, contains information only about the rms magnitude of v_p on a given scale. More information about peculiar motions in different cosmological scenarios can be obtained from other types of the velocity correlation functions that can be estimated from data sets.

As direct data on peculiar velocities of galaxies are hard to obtain, the pairwise galaxy velocity dispersion is measured from ordinary redshift surveys by modelling its effect on the redshift space correlation function. This modelling is not very certain, as it depends on the choice both of the adopted mean streaming velocity model and of the model for the pairwise velocity distribution itself. The latter is usually modelled as an exponential distribution (Peebles, 1980).

The first determination of the pairwise velocity dispersion ₁₂² was made by Davis and Peebles (1983), who found ₁₂ 340 km s^-1. Subsequent determination from the IRAS data (Fisher et al., 1994; Fisher, 1995) gave a similar value (₁₂ 317 km s^-1). These values were much lower than those predicted for the Standard Cold Dark Matter (SCDM) model (₁₂ 1000 km s^-1), and served as an argument for discarding the model.

Later determinations have given larger values for this dispersion: the estimates of Jing et al. (1998), Marzke et al. (1995), Zehavi et al. (2002) all converge at the value ₁₂ 550-600 km s^-1; not enough for the SCDM model, but in concordance with the present standard, the CDM model.

In the stable clustering model the pairwise velocity dispersion should scale with pair distance as r^0.2; this scaling has not been observed. Also, it is well known that the value of ₁₂ is sensitive to the presence of rich clusters in the sample. Davis et al. (1997) and Landy et al. (1998) propose alternative schemes for estimating the pairwise velocity dispersion, which again lead to small values of ₁₂.

The galaxy velocity field is also rather inhomogeneous; a well-known fact is the extreme coldness of the flow in our neighbourhood, out to 5 h^-1 Mpc, where ₁₂ = 60 km s^-1 (Schlegel et al., 1994).