E. Light does not trace mass

It has long been realized that there is a difference between the distribution of light in the Universe and the distribution of mass. The first clues came with the apparent systematic increase of mass-to-light ratios with scale determined from galaxies, binary galaxies, groups and clusters of galaxies: this was later made more explicit by Einasto et al. (1974), Joeveer and Einasto (1978) and Ostriker et al. (1974). It was also known that galaxy morphology is related to the clustering environment (Hubble, 1936; Zwicky, 1937; Abell, 1958; Davis and Geller, 1976; Dressler, 1980; Einasto et al., 1980; Guzzo et al., 1997).

The recognition that clustering depends on galaxy luminosity is more recent (Hamilton, 1988; Domínguez-Tenreiro and Martínez, 1989; White et al., 1988; Martínez et al., 1993; Loveday et al., 1995; Willmer et al., 1998; Benoist et al., 1999; Kerscher, 2003).

It is not difficult to understand why this should be so. We may be even surprised that the results were in any way surprising! There was early work of Bahcall and Soneira (1983), Bardeen et al. (1986), Melott and Fry (1986). However, it has not been easy to model these luminosity - and type-dependent phenomena since we have only the barest understanding of the galaxy formation process and it is probably fair to say that our knowledge of what causes galaxies to have vastly different morphologies is still rather incomplete.

The recent advances in augmenting N-body simulations with semi-analytic models and computational hydrodynamics is promising, though at a relatively early stage (Katz et al., 1992; Cen and Ostriker, 1992; Benson et al., 2000; Blanton et al., 1999; Colín et al., 1999; Kauffmann et al., 1999; Pearce et al., 1999; White et al., 2001; Yoshikawa et al., 2001). Modelling the formation of individual galaxies shows just how many physical processes must be taken into account, quite apart from trying to fold in our ignorance of the star formation process (and that is what gives rise to the luminosity). A brave attempt is exemplified by the paper of Sommer-Larsen (2003).

1. Mass distribution and galaxy distribution: biasing

The concept of biasing was introduced by Kaiser (1984) in order to explain the observed relation between the correlation functions of galaxies and galaxy clusters. Using the high-peak approximation to a Gaussian density field, he obtained a formula (26) showing that the two correlation functions were proportional.

The same idea was later applied to galaxy distributions: as different types of galaxies have different clustering properties, they cannot all follow directly the overall density field. Thus we normalize the correlations by writing

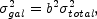(31)

(note that ² = (0)), and call b the bias factor. As baryonic matter comprises about four per cent of the total matter plus energy content of the universe, we can also say that the above relation connects the galaxy and dark matter distributions.

Bias cannot be measured directly, and indirect observational determinations of bias values have not yet converged to a single value for a given type of galaxies. Moreover, Dekel and Lahav (1999) showed that bias is, in general, nonlinear and stochastic. And later determinations have found that bias is also scale-dependent (Hamilton et al., 2000). Such bias can easily destroy scaling relations that could be inherent in the matter distribution.

2. Mass and light fluctuations

An alternative measure of the scale dependence of clustering is to plot the variance of the mass or light density fluctuations on a variety of scales. This is little more than what Carpenter had done in the 1920's, and was first formalized by Peebles (1965) in his remarkable paper on galaxy formation. ⁸ It is relatively easy to calculate a density fluctuation spectrum: sample the density field in windows of different sizes, for each window size calculate the mean and variance of the contents of the window and plot the result. This works equally well in two or three dimensions. Some important technical questions arise: what to do at the boundaries and what the shape and profile of the window should be. By the profile it is meant what weight is attached to an object falling at a given location in the window. The "top hat" profile counts a weight of one if the object is in the window and zero outside: this is the simplest choice, though not a particularly good one. Fuzzy edged windows are to be preferred since they reduce the effects of shot noise.

This process is analogous to two other methods of analyzing a density field: counts in cells and wavelet analysis. Counts in cells statistics do precisely what has just been described, using various coverings of the data set, and are most often hard-edged. The wavelet analysis does the same, but the choice of analyzing wavelet determines how "hard" the sampling volume is. Simple Haar wavelets are a bad choice since they too are hard-edged, but there are many fine alternatives. This an an area which requires more research since wavelets are particularly good at sniffing out scaling relationships.

The density fluctuation spectrum is in some sense a half-way house towards the power spectrum: the variance of the mass fluctuations are referred to a physical variable, mass scale, rather than the k-space wavenumber (which is itself an inverse length scale). The problem with the mass spectrum is that its amplitudes are correlated and depend on the adopted mass profile filter; the conventional power spectrum (spectral density) has independent amplitudes as it will be explained in Sect. VI.C.

⁸ Several things are remarkable about Peebles' 1965 paper. It was Peebles' first paper on galaxy formation and its submission to the Astrophysical Journal preceded the the announcement of the discovery of the microwave background. In that paper we see the entire roadmap for the following decades of galaxy formation theory, albeit in terms of initial isothermal fluctuations. Back.