B. Three-point correlation functions
The simplest high-order correlation function is the 3-point
correlation function 
(x1, x2,
x3). It appears to be simply related to the two-point
function through a Kirkwood-like relationship (see
Peebles (1980)):
 |
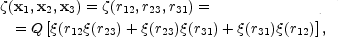(32) |
where Q 
1 is a
constant, and the first equality is due to the usual assumption of
homogeneity and isotropy. This scaling law is called "the
hierarchical model" in cosmology, and it agrees rather well with
observations. The full Kirkwood law
(Ichimaru, 1992)
would require an additional
term on the right-hand side of Eq. (32), proportional to
(r12)
(r23)
(r31).
As observations show (Peebles, 1980; Peebles, 1993; Meiksin et al., 1992), there is no intrinsic 3-point term, either Kirkwood type or more general. If this term were present the 3-point function would be enormous at small scales. Therefore it makes no contribution. The absence of such a 3-point term is probably a consequence of the fact that gravity is a two-body interaction and is the only force that plays a role in the clustering process.