C. The power spectrum
The power spectrum P(k) is the description of clustering in terms of wavenumbers k that separates the effects of different scales. If F(k) is the Fourier transform of a random field, then
 |
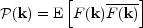(33) |
where E denotes the statistical expectation value.
The Fourier modes of a Gaussian random field (our basic model for the matter distribution in the universe at early times) are independent, and the only function that defines the field is the power spectrum. As the initial fluctuations from the inflation period are described naturally in terms of Fourier modes, the power spectrum is the best descriptor of the matter distribution for these times.
Inflationary models predict a power-law power spectrum, P(k) ~ kn (see Peebles and Ratra (2003) for a recent review), with the most popular exponent n = 1. This simple scaling is, however, broken, once the wavelength of a mode gets smaller than the horizon; interactions between matter, radiation and gravity deform the power spectrum in a computable, but complex manner (Eisenstein and Hu, 1998; 1999).
Nevertheless, if we restrict ourselves to a smaller scale interval
(say, two orders of magnitude), the power spectrum remains close
to a power law. For the scales of the observed structure the
exponent of this power law is negative, ranging from n = - 1 for
larger scales to n 
-
3 for galaxy scales.
If we combine a scale-free power spectrum P ~
kn with a scale-free expansion law a(t) ~
t
we
should get a
perfect scaling regime for evolution of structure. Unfortunately,
this is not true, as there are two completely different regimes of
evolution of gravitating structures: the linear regime, when every
Fourier mode grows at the same rate, and the nonlinear regime,
when we can assume that objects are virialized and their physical
structure does not change. The latter assumption is called
"stable clustering"
(Peebles, 1974b).
The linear regime is characterized by small density amplitudes and
large scales (small wavenumbers), the stable clustering regime has
large density amplitudes and occurs at small scales (large
wavenumbers). The scaling solution for the correlation function in
the stable clustering regime was found by
Peebles (1974b):
(r) ~
r-
, where
= (9 +
3n) / (5 + n). The first
attempt to get a solution that would interpolate between the two
regimes was made by
Hamilton et al. (1991).
For that they rescaled the
distances r, assuming no shell crossing during evolution of
objects, and found an empirical relation between the nonlinear and
linear correlation functions, using N-body models. This is known
as the HKLM scaling solution.
Peacock and Dodds (1996)
found a similar
relation for power spectra. These results have been used
frequently for likelihood search in large volumes of cosmological
parameter space, which could not be covered by time-consuming
N-body modelling.
However, nowadays it seems that the stable clustering hypothesis does not describe well either the observed structure, or present-day numerical simulations, mostly because of merging of objects in the later stages of evolution of structure. A scaling solution in terms of a nonlinearity wavenumber that does not assume stable clustering is described by Smith et al. (2003). Let us define the nonlinearity wavenumber kNL by
 |
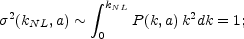it separates the linear regime k < kNL from the nonlinear regime k > kNL. One then expects the scaling solution to have the form
 |
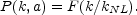As an example, for the Einstein-de Sitter cosmological model a(t) ~ t2/3, the scale-free power spectrum can be written as P(k, a) = a2 kn, and the nonlinearity wavenumber kNL ~ a-2/(n+3). Numerical experiments confirm that scaling solutions exist.
The latest real-space power spectrum of the SDSS survey (Tegmark et al., 2004) shows clearly curvature, departing from a single power-law, providing, as the authors say, "another nail into the coffin of the fractal universe hypothesis".