D. The bispectrum

The power spectrum (Eq. 33) is a quadratic descriptor of a random field: it contains information about the amplitudes of the Fourier components, but not about any phase relationships that might have evolved through nonlinear processes. The power spectrum characterizes fully a Gaussian field. Since the present-day high-amplitude fluctuating density field is not Gaussian (there cannot be any region with negative density), the power spectrum by itself is provides only a partial description. There are several ways of providing further information in Fourier space, one of which is to look at higher order correlations among Fourier components.

The next order descriptors are cubic, the three-point correlation function and its Fourier counterpart, the bispectrum. The bispectrum is the third moment of the Fourier amplitudes of a random field, depending on three wavenumbers. If we denote the Fourier amplitudes of a random field by F(k), the bispectrum of the field is defined as

where E denotes the statistical expectation value. For homogeneous random fields the bispectrum is non-zero only for closed triangles of vectors k₁, k₂, k₃ (see, e.g., Martinez and Saar (2002)). Consequently, for real-valued homogeneous random fields the bispectrum can be calculated by

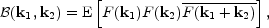where the overline denotes conjugation. In the signal processing world the bispectrum is known as the bicoherence spectrum and it is used to measure the phase coherence among triples of spectral components that arises as a consequence of nonlinear wave coupling.

The hierarchical ansatz that we wrote for the three-point correlation function can be written also for the bi-spectrum:

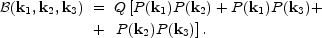A similar expression is predicted by perturbation theory (Fry, 1984b), but with different coefficients for every term.

It is not easy to determine the bi-spectrum from observations, as its argument space is large (the set of all triangles), and it is strongly modified by galaxy bias. The estimates so far have confirmed that the bispectrum follows approximately the predictions of the perturbation theory (Bernardeau et al., 2002). As it depends on the bias parameters, it can be used to estimate galaxy bias. An example is provided by a recent study (Verde et al., 2002) that found that the bi-spectrum of the 2dFGRS galaxies is compatible with no bias; these galaxies seem to faithfully trace the total matter distribution.