


The simplest way to explain the observed clustering is to do nonlinear numerical simulations of the galaxy clustering process. Although such simulations provide no deep explanations for what is going on, the ability to reproduce cosmic clustering simply by using a distribution of particles moving under their mutual gravitational interactions is quite striking.
N-body models have served to disprove several popular hypotheses on the evolution of large-scale structure, and motivated to introduce new assumptions. The downfall of the "Standard Cold Dark Matter Model" (SCDM) started with N-body models that gave top-heavy large-scale structure and too large pairwise velocity dispersion compared to the observations. Another example is the present controversy over cuspy centers of dark halos, which were found in high-resolution N-body simulations, but which are not observed. This motivated intensive study of Warm Dark Matter models.
The origin of N-body experiments as we know them today is the work of Sverre Aarseth at Cambridge England (Aarseth, 1978). Aarseth was a student of Fred Hoyle whose visionary insight foresaw as long ago as 1965 the role that computers would play in astronomical research. Aarseth not only developed series of N-body codes tailor-made for different problems, he made these codes available to all and never even asked to be named as a collaborator.
The particle-particle codes developed by Aarseth were originally aimed at simulating problems in stellar dynamics. The particles were point masses and integrating of tight binaries was through two-body regularization. This was adapted to the cosmological problem by making the particles soft rather than point-like, and so dropping the need for the time-consuming calculation of binary encounters. The first papers using this modified code (Aarseth et al., 1979; Gott et al., 1979) used a mere 1000 equal mass particles and simple Poisson initial conditions. Yet they were able to reproduce a power-law correlation function for the clustering of these points.
During the 1970's the application of N-body codes to the problem of gravitational clustering mushroomed. Faster computers and improved numerical techniques drove particle numbers up. Following on from that work there has been a gradual growth in the number of particles used in simulations: 30,000 by the 1980s (Efstathiou et al., 1985), 1,000,000 by Bertschinger and Gelb (1991) in the 1990s (see also the review Bertschinger (1998)) and Couchman et al. (1995), and now more than 1000,000,000 by the "Virgo Consortium" (Evrard et al., 2002).
The N-body models cover a wide range of cosmic parameters and have enough particles to be used in trying to discriminate the clustering properties of the different models. We show in Fig. 17 a recent 109-point lightcone simulation of the "Virgo Consortium", a deep wedge 40 h-1 Mpc thick and 3.5 h-1 Gpc deep, extending to z = 4.8 (the universe was then about one eleventh of its present age). The upper sector of the "tie" shows a picture that we hope to get from the SDSS survey, a wider wedge reaching z = 0.25. Progressing in time from the largest redshift until present, we see how the structure gradually emerges. This simulation is described in Evrard et al. (2002).
 |
Figure 17. A deep simulated wedge of the Universe. Figure by Gus Evrard and Andrzej Kudlicki, courtesy of the "Virgo Consortium"; details in text. |
Sometimes we might get the impression that N-Body simulations are better than the real thing, as in the game of `Better Than Life' played by some of the characters in the BBC TV program Red Dwarf. In the early 1970's people were enthusiastic about a mere 1000 particles (which reproduced the correct two-point correlation function so "it had to be right"). They got even more enthusiastic with a million particles in the 1990's and now it is indeed better than life, especially with reality enhancing graphics, and ready-to-play in your PowerPoint presentation movies.
Is this enthusiasm justified? N-Body simulations are certainly a success story, and they certainly make a huge contribution to our understanding of cosmology. The models are nevertheless extremely limited simply because they lack any real gasdynamics, and star formation which must be important or other things that we know little about (such as magnetic fields, which one hopes are not important). There are some salutary lessons, such as the effects of discreteness in pure N-Body models (Splinter et al. (1998)), but there is little or no response to such points from the N-Body community at large. So maybe we should not worry and just bask in what is after all better than life.
Up until now, most comparisons between the results of numerical experiments and the data have been made simply in terms of the galaxy clustering correlation function. Even this is fraught with difficulty since the observed data concerns the distribution of light whereas the numerical models most readily yield the clustering properties of the gravitating matter, most of which may well be dark and invisible. The key ingredient that has to be added is star formation, and it is perhaps true to say that attempts at doing this have so far been simple heuristic first steps.
Another popular model result, the mass function (distribution of masses) of rich galaxy clusters, depends less on star formation problems, but knowledge of formation of galaxies and clusters is certainly necessary to compare the simulated and observed mass functions.
Some measures, such as the distribution of velocity dispersion of galaxies and the distribution of halo masses are independent of the mass-to-light problem, but it is only recently that the large scale redshift surveys and surveys of real gravitational lenses have begun to yield the kind of data that is required.
4. Scaling in dark matter halos
N-body simulations have revealed fascinating scaling problems of their own, mostly for smaller scales than those described in this review. As the initial power spectrum of perturbations is almost a power law for comoving scales less than 10 h-1 Mpc, and cold dark matter and gravitation do not bring in additional scales, the evolution of structure on these scales, and the final structure of objects should be similar.
As a proof of this conjecture, N-body simulations show that dark matter halos have well-defined universal density profiles. There is slight disagreement between the practitioners on the exact form of this profile, but the most popular density profile by far is that found by Navarro et al. (1996) (the NFW profile):
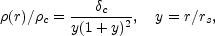 |
(52) |
where
 c is
the critical cosmological density,
c is
the critical cosmological density,
 c a
characteristic density contrast, and rs is a scale
radius. The
masses of N-body halos are usually defined as that contained
within the "virial radius" r200, the radius of a sphere of
mean density contrast 200. Then the only parameter describing the
NFW profile for a halo of given mass is the concentration ratio
c = r200 / rs.
c a
characteristic density contrast, and rs is a scale
radius. The
masses of N-body halos are usually defined as that contained
within the "virial radius" r200, the radius of a sphere of
mean density contrast 200. Then the only parameter describing the
NFW profile for a halo of given mass is the concentration ratio
c = r200 / rs.
There have been many studies with differing conclusions on the exact properties of dark halo profiles; we shall refer the reader to the latest accurate analysis (Navarro et al., 2004). The main difficulty is in eliminating a multitude of possible numerical artifacts, but nobody seems to doubt that universal profiles exist. Concentration ratios depend on the mass of a halo, but this seems to be the main difference.
In connection with observations, the main problem has been the existence of a density cusp in the center of a halo, and the value for the logarithmic slope. As this demands probing the very central regions of galaxy clusters and galaxies, the problem is still open.
5. Scaling in galaxy properties
While the notion of the universal density profile arose from
N-body simulations, other scaling laws for cluster- and
galaxy-sized objects have observational origin. The best established
law is called the Fundamental Plane (FP). This scaling law was
discovered simultaneously by
Djorgovski and
Davis (1987) and
Dressler et
al. (1987).
It is rather complex, meaning that elliptical
and S0 (early-type) galaxies form a plane in the 3-space of
(log L, log rc,
log ), where L is
the total luminosity of the
galaxy, rc is its characteristic radius and
), where L is
the total luminosity of the
galaxy, rc is its characteristic radius and
 2 its
stellar velocity dispersion. (As L and rc can
be combined to give
< I >c, the mean surface brightness of the
galaxy, the latter is frequently chosen as one of the three
variables.) These properties of elliptical galaxies are tightly
correlated, and are thought to describe the process of their
formation. Similar correlations have been discovered for galaxy clusters
(Lanzoni et
al., 2004).
Their existence demands special scaling
for the mass-luminosity ratio of cluster galaxies with the mass of
the cluster.
2 its
stellar velocity dispersion. (As L and rc can
be combined to give
< I >c, the mean surface brightness of the
galaxy, the latter is frequently chosen as one of the three
variables.) These properties of elliptical galaxies are tightly
correlated, and are thought to describe the process of their
formation. Similar correlations have been discovered for galaxy clusters
(Lanzoni et
al., 2004).
Their existence demands special scaling
for the mass-luminosity ratio of cluster galaxies with the mass of
the cluster.
As the fundamental plane relation contains the size of a galaxy, it can be used for estimating the distance to a galaxy. Having a distance estimate, we can disentangle the proper velocity of a galaxy from that of the Hubble flow. Dressler et al. (1987) ("the Seven Samurai") used the newly discovered fundamental plane relation to derive for the first time the nearby large-scale galaxy velocity field. In this way the "Great Attractor", a large supercluster complex partly hidden by the Milky Way, was predicted by Lilje et al. (1986) from a relatively local sample of galaxies and discovered by Lynden-Bell et al. (1988) using a larger sample of elliptical galaxies. A recent example of a similar project is the NFP Survey (NOAO Fundamental Plane Survey), a survey of 100 rich X-ray selected clusters within 200 h-1, where the fundamental plane of early-type cluster galaxies is used to determine cluster distances and, therefore, large scale cluster flows (Nelan et al. (2003)).
When talking about scaling laws at galaxy and cluster scales, one cannot bypass the well-known Tully-Fisher (Tully and Fisher, 1977) and Faber-Jackson (Faber and Jackson, 1976) scalings, which declare that the luminosities (or masses) of galaxies are tightly correlated with their velocity spread. These scalings can be written as:
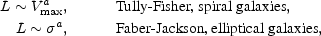 |
where Vmax is the maximum rotation velocity of a
spiral galaxy,
and  2 is the
stellar velocity dispersion of an elliptical galaxy
(in fact, the fundamental plane relation previously explained
is a refinement of the Faber-Jackson relation). The power-law exponent
a
2 is the
stellar velocity dispersion of an elliptical galaxy
(in fact, the fundamental plane relation previously explained
is a refinement of the Faber-Jackson relation). The power-law exponent
a  4, which can
be easily explained,
if there are no dark matter halos around galaxies, and is
difficult to explain for the CDM paradigm. This difficulty has
been of strong support for the MOND theory
(Milgrom, 1983).
This theory substitutes the Newtonian theory in the limit of small
accelerations by an empirical formula, which explains the flat
rotating curves of galaxies without invoking the notion of
dark matter, and explains naturally the Tully-Fisher scaling.
MOND does not fit into the present picture of
fundamental physics, as the CDM assumption does,
but it has found a number of followers. A critical (but well-meant)
assessment of MOND can be found in a recent review by
Binney (2003).
4, which can
be easily explained,
if there are no dark matter halos around galaxies, and is
difficult to explain for the CDM paradigm. This difficulty has
been of strong support for the MOND theory
(Milgrom, 1983).
This theory substitutes the Newtonian theory in the limit of small
accelerations by an empirical formula, which explains the flat
rotating curves of galaxies without invoking the notion of
dark matter, and explains naturally the Tully-Fisher scaling.
MOND does not fit into the present picture of
fundamental physics, as the CDM assumption does,
but it has found a number of followers. A critical (but well-meant)
assessment of MOND can be found in a recent review by
Binney (2003).