


B. Statistical models
The earliest models of galaxy clustering were based on Charlier's simple notion that the system of galaxies formed some kind of simple hierarchy. There was little or no observational basis for such models. Later on, in the 1950's when galaxy clusters were seen as objects in their own right, the clustering process was seen as aggregates of points (the clusters) scattered randomly in an otherwise uniform background.
It was not until the systematic analysis of galaxy catalogs and the discovery of that the two-point clustering correlation function is a power law that the distribution of galaxies was seen as being a consequence of gravitational aggregation on all scales. Galaxy clustering was a general phenomenon and rich galaxy clusters were seen as something rather rare and special, but nevertheless a part of the overall clustering process.
One of the most important of the early attempts to model the galaxy clustering process came from the Berkeley statisticians Neyman and Scott (1952). They sought to model the distribution of galaxy clusters as a random spatial superposition of groups of galaxies of varying size. The individual groups were to have their galaxies distributed in a Gaussian density distribution and they found evidence of superclusters (Neyman et al., 1953).
Whereas the model in that early form had limited application for cosmology, the Neyman-Scott process became a discipline in its own right. It remains to be seen whether a generalization of these processes might be resurrected for present day clustering studies. A recent program in a similar vein is called the halo model; we shall describe it below.
There has for a long time been a strong interest in the theory of random processes which has had a strong impact on many fields of physics (see for example the collection of classic papers by Wax (1954)). Among the simplest of random processes is the so-called "Random Walk" in which a particle continually moves a random distance in a random direction subject to a set of simple rules. The collection of points at which the particle stops before moving on has a distribution that can often be calculated.
Many random walks result in distributions of points that are clustered. The character of the clustering depends on the conditions of the walk. It did not take long before someone suggested that the galaxy distribution could be modeled by a random walk (Fournier d'Albe, 1907; Mandelbrot, 1975).
What was of interest in these random walk models is that they could be characterized by a single parameter: a power law index that related to the mean density profile of the point distribution.
It should be noted that these simple fractal models have little direct interest in cosmology: they are merely particularly simple examples of clustering processes among many. In particular they do not show the transition to cosmic homogeneity on large scales and have no relevant dynamical content.
That is not to say that one cannot construct relevant fractal models. By 'relevant' we mean that the model should at least be consistent with or derived from some dynamical theory for the clustering: anything else is merely descriptive. Some relevant ones are described below.
3. More complex clustering models
It was clear at an early stage that the two-point correlation function for galaxy clustering was by itself an incomplete descriptor of the galaxy distribution: quite different point distributions can have the same two-point correlation function.
The obvious step was to compute 3-point and higher order correlation functions and to seek a more complete description of the clustering that way. The key discovery was that the higher order functions could all be expressed as sums of products of two-point correlation functions alone. This lead to a quest to build clustering hierarchies that embodied these important scaling properties.
It was evident at the outset that such models would have to be more sophisticated than the simple fractal hierarchy of Mandelbrot. The first such model was the clustering hierarchy (a bounded fractal) of Soneira and Peebles (1978). This model produced a galaxy distribution looking remarkably like the observed galaxy distribution.
The observation that the galaxy distribution was a clustering hierarchy in which all orders of correlation function could be related to the basic two-point function could be described in another way. Instead of using just one power law index, as in a simple fractal, to describe the clustering process, it might be possible to use a distribution of power laws. This gave rise to the multifractal model of Jones et al. (1988) in which the distribution could be generated by a set of simple scaling laws.
The Voronoi tessellation, and the related Delaunay tessellation, provide well-known tools for investigations into clustering in point processes. The construction of such a tessellation starts from a set of seed points distributed randomly according to some rule (often Poisson distributed). A set of walls is constructed around each point defining a closed polyhedron. Every point in the polyhedron has the original seed point as its nearest point among the set of all seeds.
The polyhedron effectively defines a volume of influence for each seed point. The vertices of these polyhedra define a set of points that is also randomly distributed, but in a way that is quite different from the distribution of the original seeds.
These tessellations were introduced into astronomy by Icke and van de Weygaert (1987) as a model for the galaxy clustering process. Detailed description of two-dimensional Voronoi tessellations can be found in Ripley (1981). The best sources of information on 3-dimensional tessellations in general and in cosmology are van de Weygaert (1991, 2002).
What is remarkable is that the two point correlation function for the Voronoi Vertices generated from Poisson distributed seeds is a power law that is close to the observed power law of the two-point galaxy correlation function (see Fig. 18). This tessellation thereby provides a possible model for the observed galaxy distribution.
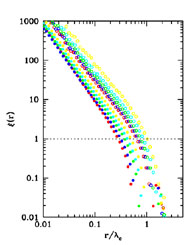 |
Figure 18. The scaling of the two-point correlation function is shown for different subsamples of a Voronoi vertices model. The subsamples have been selected according to given "richness" criterium that mimic that of the real galaxy cluters, from van de Weygaert (2003). |
Galaxies appear to form on filaments and sheets that surround void regions. If in the Voronoi model we regard the original seeds as the centers of expansion of cosmic voids, this model becomes a dynamically plausible nonlinear model for the formation large-scale structure formation (van de Weygaert and Icke, 1989). The resulting galaxy distribution has many interesting features that seem to accord with the distribution of galaxies in redshift surveys (Goldwirth et al., 1995).
5. Lognormal models and the like
A rather simplistic yet effective model was presented by
Coles and Jones
(1991)
who postulated that the originally Gaussian
density field would evolve into a log-normally distributed density
field. The motivation for this was simply that the hydrodynamic
continuity equation implied that
log would be
normally
distributed if the velocity field remained Gaussian. The counts in
cells of various size for N-body models and for catalogs of
galaxies are indeed approximately log-normal for a variety of cell volumes.
would be
normally
distributed if the velocity field remained Gaussian. The counts in
cells of various size for N-body models and for catalogs of
galaxies are indeed approximately log-normal for a variety of cell volumes.
Clearly, the contours where the density equaled the mean would remain fixed: there is no dynamics in such a model. Such a naive approach could never reproduce the structure we see today.
There are several relatively simple generalizations of the lognormal distribution, notably the Poisson lognormal (Borgani, 1993) and the negative binomial distribution (Elizalde and Gaztañaga, 1992; Betancort-Rijo, 2000).
A novel set of distribution functions was introduced by Saslaw and Seth (1993) and Sheth and Saslaw (1996) derived from a thermodynamic description of the clustering process. The distribution functions describe the probability that a randomly chosen sample volume contains precisely N galaxies. There is only one free parameter in terms of which the count distribution for arbitrary values of the volume can be fitted. The resulting fit is quite remarkable for both N-body experiments and for the data sets that have been analysed (Saslaw and Crane, 1991).
The distribution function has some interesting scaling properties that are discussed in Saslaw (2000).
Given the quality of the fit to the data, this is clearly a model in which the underlying physical motivation deserves more attention.
An alternative approach is to create a model for the evolution some statistically important quantities. Balian and Schaeffer (1989a) selected the Void Probability Function: the probability that a volume V chosen at random would contain no points (galaxies). This can be generalized to discuss the probability distributions of volumes containing 1, 2 or N galaxies.
Balian and Shaeffer were able to express many of the details of the clustering hierarchy in terms of the Void Probability function, in particular they found a bifractal behavior for the galaxy distribution (Balian and Schaeffer, 1989b). Scaling of voids as a test of fractality has been studied by Gaite and Manrubia (2002).
The mass (luminosity) function was also derived from similar scaling arguments by Bernardeau and Schaeffer (1991), who found the scaling between the galaxy and cluster luminosity functions to support the theory of Balian and Schaeffer (1989b).
Vergassola et al. (1994) attacked the problem of gravitational evolution of hierarchical (fractal) initial conditions. They choose the adhesion approximation to describe the gravitational dynamics and demonstrated (with much greater rigour than usual in cosmological papers) that the mass function has two scaling regimes, defined by the scaling exponent of the initial velocity field. This is the only paper that explicitly describes the evolution of structure on all, even infinitesimally small scales.