


C. Dynamical models
The earliest attempt to explain the apparent power law nature of the two point galaxy correlation function was due to Peebbles (1974a, b) and to Gott and Rees (1975). These models were based on the simple idea that a succession of scales would collapse out of the expanding background and then settle into some kind of virial equilibrium. The input data for the model was a power law spectrum of primordial imhomogeneities and the output was a power law correlation function on those scales that had achieved virial equilibrium. There would, according to this model, be another power law on larger scales that had not yet achieved virial equilibrium.
For a primordial spectrum of the form
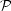 (k)
(k)
 k-n
the slope of the two-point galaxy correlation function would be
k-n
the slope of the two-point galaxy correlation function would be
 =
(3n + 9) / (n + 5), which for n = 0 gave a respectable
=
(3n + 9) / (n + 5), which for n = 0 gave a respectable
 = 1.8,
while n = 1 gave an almost respectable
= 1.8,
while n = 1 gave an almost respectable
 = 2.
= 2.
The apparent success of such an elementary model gave great impetus to the field: we saw something we had some hope of understanding. However, there were several fundamental flaws in the underlying assumptions, not the least of which was that the observed clustering power law extended to such large scales that virial equilibrium was out of the question. There were also complications arising out of the use of spherical collapse models for calculating densities.
Addressing these problems gave rise to a plethora of papers on this subject, too numerous to detail here. A fine modern attempt at this is Sheth and Tormen (1999). The subject has since evolved into some of the more sophisticated models for the evolution of large scale structure that are discussed later (e.g. Sheth and van de Weygaert (2004)).
Cosmic structure grows by the action of gravitational forces on finite amplitude initial density fluctuations with a given power spectrum. We see these fluctuations in the COBE anisotropy maps and we believe they are Gaussian. This means that the initial conditions are described as a random process with a given two-point correlation function. There are no other higher order correlations: these must grow as a consequence of dynamical processes.
Given that, it is natural to try to model the initial growth of the clustering via a BBGKY hierarchy of equations which describe the growth of the higher order correlation functions. The first attempt in this direction was made by Fall and Severne (1976) though the paper by Davis and Peebles (1977) has certainly been more influential. The full BBGKY theory of structure formation in cosmology is described in Peebles (1980) and in a series of papers by Fry (Fry, 1982; 1984a). Fry (1985) predicted the 1-point density distribution function in the BBGKY theory. He also developed the perturbation theory of structure formation (Fry, 1984b), which has become popular again (see the recent review by Bernardeau et al. (2002)).
In the perturbative approach, the main question is how many orders of perturbation theory are required to give sensible results in the nonlinear regime.
3. Pancake and adhesion models
Very early in the study of clustering, Zel'dovich (1970) presented a remarkably simple, yet effective, model for the evolution of galaxy clustering. In that model, the gravitational potential in which the galaxies moved was considered to be known at all times in terms of the initial conditions. The particles (galaxies) then moved kinematically in this field without modifying it. They were in effect test particles with no self-gravity. The equations of motion were arranged so as to give the correct initial, small amplitude, linear approximation result.
The Zel'dovich model provided a first glimpse of the possible growth of large scale cosmic structure and led to the prediction that the galaxy distribution would consist of narrow filaments of galaxies surrounding large voids. Nothing of the sort had been observed at the time, but striking confirmation was later achieved by the CfA-II Slice sample of de Lapparent et al. (1986) whose redshift survey revealed for the first time remarkable structures of the kind predicted by Zel'dovich.
In order to make further progress it was necessary to cure one problem with the Zel'dovich model: the filaments formed at one specific instance and then dissolved. The dissolution of the filaments happened because there was nothing to bind the particles to the filaments: after the particles entered a filament, they left. The cure was simple: make the particles sticky. This gave rise to a new series of models, referred to a "adhesion models" (Gurbatov et al., 1989a; Kofman et al., 1992). They were based around the three dimensional Burgers equation. In these models structure formed and once it formed it stayed put: the lack of self gravity within these models prevented taking them any further.
It was, however, possible to compute the scaling indices for various physical quantities in the adhesion model. This was achieved by Jones (1999) using path integrals to solve the relevant version of the Burgers equation.
Peebles (1985) first recognized that power law clustering might be described by a renormalization group approach in which each part of the Universe behaves as a rescaled version of the large part of the Universe in which it is embedded. This allows for a recursive method of generating cosmic structure, the outcome of which is a power law correlation function that is consistent with the dynamics of the clustering process.
Peebles (1985) used this approach for numerical simulations of the evolution of structure, hoping that the renormalization approach would complement the usual N-body methods, improving the usually insufficient spatial resolution and helping to get rid of the transients caused by imperfect initial conditions. The first numerical renormalization model had only 1000 particles and suffered from serious shot noise.
This was later repeated on a much larger scale by Couchman and Peebles (1998). As before, they found that the renormalization solution produces a stable correlation function. However, the spatial structures generated by the renormalization algorithm differed from those obtained by the conventional test simulation. The relative velocity dispersion was smaller, and the mass distribution of groups was different. As a rule, the renormalization solution described small scales better, and the conventional solution was a better description of the large-scale structure. As both approaches, the conventional and the renormalization procedures, suffer from numerical difficulties, the question of a true simulation remains open.
5. The halo model and PThalo model
The early statistical model (Neyman and Scott, 1952) for the galaxy distribution assumed Poissonian distribution of clusters of galaxies. This model was resurrected by Scherrer and Bertschinger (1991) and has found wide popularity in recent years (see the review by Cooray and Sheth (2002)). In its present incarnation, the halo model describes nonlinear structures as virialized dark matter halos of different mass, placing them in space according to the linear large-scale density field that is completely described by the initial power spectrum. Such substitution is shown in Fig. 19, where the exact nonlinear model matter distribution is compared with its halo model representation.
 |
Figure 19. The halo model. The simulated dark matter distribution (left panel) and its halo model (right panel), from Cooray and Sheth (2002). |
Once the model for dark matter distribution has been created, the halos can be populated by galaxies, following different recipes. This approach has been surprisingly fruitful, allowing calculation of the correlation functions and power spectra, prediction of gravitational lensing effects, etc. This also tells us that low-order (or any-order) correlations cannot be the final truth, as the two panels in Fig. 19 are manifestly different.
The success of the (statistical) halo model motivated a new dynamical model to describe the evolution of structure (Scoccimarro and Sheth, 2002). The PTHalos formalism, as it is called, creates the large-scale structure using a second order Lagrangian perturbation theory (PT) to derive the positions and velocities of particles, and collects then particles into virialized halos, just as in the halo model. As this approach is much faster than the conventional N-body simulations, it can be used to sample large parameter spaces - a necessary requirement for application of maximum likelihood methods.
Two analytic models in the spirit of the Press-Schechter density patch model are particuarly noteworthy: the "Peak Patch" model of Bond and Myers (Bond and Myers, 1996a, 1996b, 1996c) and the very recent "Void Hierarchy" model of Sheth and van de Weygaert (2004).
Both of these models attempt to model the evolution of structure by breaking down the structure into elements whose individual evolution is understood in terms of a relatively simple model. The overall picture is then synthesized by combining these elements according to some recipe. This last synthesis step is in both cases highly complex, but it is this last step that extends these works far beyond other like-minded approaches and that lends these models their high degree of credibility.
The Peak Patch approach is to look at density enhancements, while the Void Hierarchy approach focusses on the density deficits that are likely to become voids or are embedded in regions that will become overdensities. It somewhat surprising that Peak Patch did not stimulate further work since, despite its complexity, it is obviously a good way to go if one wishes to understand the evolution of denser structures.
The Void Hierarchy approach seems to be particularly strong when it comes to explaining how large scale structure has evolved: it views the evolution of large scale structure as being dominated by a complex hierarchy of voids expanding to push matter around and so organize it into the observe large scale structures. At any cosmic epoch the voids have a size distribution which is well-peaked about a characteristic void size which evolves self-similarly in time.