E. Nonlinear dynamic models
The Zel'dovich approximation and its fixups are Lagrangian descriptions of the cosmic fluid flow. Their importance lies in the fact that they capture the gross elements of the nonlinear clustering while their weakness lies in their side-stepping any real gravitational forces. Consequently, they have been used mainly as short-cut simulators of the evolution of large scale structure. Little analytic work has been done using these approaches.
It is the Lagrangian nature of those equations that makes it difficult to perform analytic calculations that might lead to an understanding of how, say, the two-point correlation function evolves with time. In order to make progress on an analytic front it is necessary to cast the equations into analytically tractable Eulerian forms. The basis for this was provided by the important "adhesion approximation" of Gurbatov et al. (1989b), though in the form presented there it was only ever used for numerical simulations.
The paper by Gurbatov et al. (1989b) provided a version of the Zel'dovich approximation in which particle shell-crossing was inhibited: the material was stopped as it approached the pancakes by an artificial viscosity introduced on a fairly ad hoc basis into the equations. The underlying equation in this approximation turns out to be the three dimensional Burgers Equation, and so the approach has the virtues of being simple to use and very easy to compute (see for example Weinberg and Gunn (1990)).
The adhesion approximation is in a sense a linear approximation: it is allowed to evolve into the nonlinear regime in the expectation that its behavior will mimic the nonlinear behavior. This shortcoming has recently been tackled by Menci (2002).
Just as the simple Zel'dovich approximation tends to diffuse the pancakes, the adhesion approximation ensures that asymptotically they are infinitely thin, and that the particle velocity perpendicular to these surfaces is zero. The slowing down of the particles as they approach the pancakes, the notion of "viscosity" in dark matter, and the lack of a full treatment of the gravitational field fluctuations leaves open some questions as to just how good the approximation is for studying, say, large scale cosmic flow fields.
It is remarkable how much can be done within the framework of the adhesion model. Babul and Starkman (1992) had introduced structure functions based on the moments of inertia of the local particle distribution, to describe the local shape of the matter distribution. They showed this to be a useful descriptor of the topology of the galaxy distribution. The evolution of these structure functions was studied analytically by Sathyaprakash et al. (1996). They analyzed the emergence of large scale filamentary and pancake-like structures and showed how this might lead to a large scale coherence in the galaxy distribution. Sahni et al. (1994) discussed the evolution of voids using the adhesion approximation. In their model, ever larger voids emerge at successive epochs, eventually leaving the largest voids. According to this model, voids contain some internal filamentary and pancake-like substructures that dissolve as the voids get older.
The random heat equation was introduced into the subject of cosmic
structure evolution by
Jones (1999).
The Bernoulli equation (59), modified by introducing viscosity (see
Jones (1999)),
can be linearised by means of the
Hopf-Cole transformation of variables in which we replace the
velocity potential
with a logarithmic velocity
potential 
:
 |
(62) |
If the gravitational potential is rescaled with the viscosity:
 |
(63) |
Equation (59) with the viscosity term reduces to
 |
(64) |
Again, it is worth stressing that
can depend on time, but we
see that invoking a time dependence in
means that the new
potential
(x) gains an
explicit time dependence.
This time dependence can be masked so as to give the random heat equation in its standard form:
 |
(65) |
It is now to be understood that either
or
(or both)
may contain an explicit time dependence through a multiplying factor.
The renormalised potential field
(x) is
considered as given and the task is to find the potential
.
This equation is familiar in slightly different forms in a variety
of fields of physics where it has a variety of names: the Anderson
Model, the Landau-Ginzburg equation, and with a complex time it is
simply the Schrodinger Equation of quantum mechanics. We may hope
to benefit from the vast knowledge that already exists about this equation.
If we take the limit
0 and use the
definition =
- 2
ln, we are led
straight back to the familiar looking dynamical equation
 |
telling us that the gravitational potential drives the fluctuating velocity field. Despite the circuitous route used in deriving the random heat equation, it still remains very close to the fundamental physical process that drives the growth of the large scale structure.
3. The Solution of the RH equation
We can formally solve random heat equation following the discussion of Brax (1992) (but see also Zel'dovich et al. (1985, 1987)). The solution is expressed in terms of path integrals as was first given by Feynman and Kac:
 |
where the propagator K is
 |
(66) |
and
 |
is the action. This is just the "free particle" action with an
additional contribution to the action from the potential
(x, t)
evaluated at appropriate places along
the various paths that contribute to the solution
(Brax (1992)).
The integrand is just the Lagrangian for a
particle moving in a potential
(x, t).
What is important here is that the potential
(x, t)
contributes to the sum over all paths through an
exponential. Thus the additive contributions from each part of
the relevant paths results in a multiplicative contribution to the
final solution. It is this which creates the lognormal
distribution in
(x,
t) if the potential
(x, t)
in normally distributed.
Zel'dovich et al. (1985,
1987)
explain the solution
(x,
t) in straightforward terms. They point out that, of all the
paths that contribute to the integral, one might expect the
dominant contribution to come from those paths that pass rapidly
through high maxima of this potential. However, there are rarer
paths (optimal trajectories) that are traversed more quickly and
so probe a greater volume that can encounter still larger (and
rarer) maxima of the potential. These latter paths in fact make
the main contribution to the integral. This is presented rigorously by
Gärtner and
Molchanov (1992).
The outcome of the discussion is that the moments of the
distribution of
scale as
 |
(67) |
where 
and
are the mean and
variance of the process
. This gives
intermittency indices
 |
(68) |
(Brax, 1992),
where the constant of proportionality is determined
by the dimensional characteristics of the random process
(x). Thus the
solution of the random heat equation is lognormally distributed for a
Gaussian fluctuating gravitational potential.
In view of the Hopf-Cole transformation, the velocity potential is
in fact the logarithm of the pseudo-potential
:
=
- 2
ln. Since
is lognormally
distributed, it follows that
is normally distributed
and we can compute its rms error as
 |
(69) |
Remember that the variance of the gravitational potential fluctuations
2
may itself
have a time dependence.
This is one of the things that was assumed as given and which in
the single-component model is given by the approximation used to
eliminate the Poisson equation.
Starting with the coupled Klein-Gordon and Einstein field equations, Widrow and Kaiser (1993) produced an ansatz for replacing the Euler and continuity equations of hydrodynamics with a Schrodinger equation in the form
 |
(70) |
(see also
Speigel (1980)).
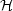here is taken to be an
adjustable parameter controlling spatial resolution. In this
model the gravitational potential and density fields are given by
 |
(71) |
Widrow and Kaiser (1993) see this as a means for doing numerical simulations of the evolution of large scale structure (they use a Schrodinger solver based on an implicit finite differencing method called Cayley's Scheme).
The Schrodinger equation for
can be solved
analytically by identical procedures to those described above for
solving the random heat equation, the difference being that the potential
being
solved is complex. is
directly related to the density field. This route is advocated by
Coles (2002)
in his very clear discussion of models for the origin of spatial
intermittency.
Coles and Spencer
(2003)
have taken this further and shown how to add
effects of gas pressure corresponding to a polytropic equation of
state. They present this as a useful approach for modeling the
growth of fluctuations in the mildly nonlinear regime, which is
somewhat short of the ambition of the original
Jones (1999) program.
The relative merits of the random heat equation and the
Schrodinger equation approach are yet to be assessed. They are
derived from quite different premises: one pretends to be a
derivation from the basic equations while the other is an ansatz
based on interpreting quantum mechanics as a fluid process. Each
has a level of arbitrariness: one involves an unknown (unphysical)
viscosity that is allowed to tend to zero, while the other
involves a tuning parameter, the effective Planck Constant
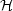that can probably be
allowed to become vanishingly small without changing any results.
In condensed matter physics generalizations of both equations have played important roles as the basis of analytic models for a diversity of physical phenomena. They appear to offer an important jumping off point for further research based on well established techniques.
More recently, Matarrese and Mohayaee (2002) have presented a modification of the adhesion model that they call the forced adhesion model. This is based on the forced Burgers equation, which they transform into a random heat equation and solve using path integrals. It should be noted that this approach is in fact quite different from that of Jones (1999): Matarrese and Moyahaee use different variables and they claim to model the self-gravity of the system, thereby avoiding Jones' external field approximation.
Menci (2002), in an approach rather similar to Matarrese and Moyahaee, also avoids the external field assumption. This is done by generalizing the simplistic gravitational terms of the classical adhesion model to a form that, it is claimed, extends the validity of the gravitational field terms. Despite the greater complexity, a solution can be achieved via path integrals.
The main shortcoming of the Jones (1999) model is indeed the assumption of an externally specified random gravitational potential field, though it is not clear that the proposed alternatives are much better. In the Jones model the intention had been to write two equations: one collisionless representing dark matter and providing the main contribution to the gravitational potential and the other collisional, representing the baryonic (dissipative) component. That program was never completed.